Note: The contents of these manuscripts are the IP of the authors, and may not be reproduced, presented to funding agencies or private foundations or in other presentations without attribution.
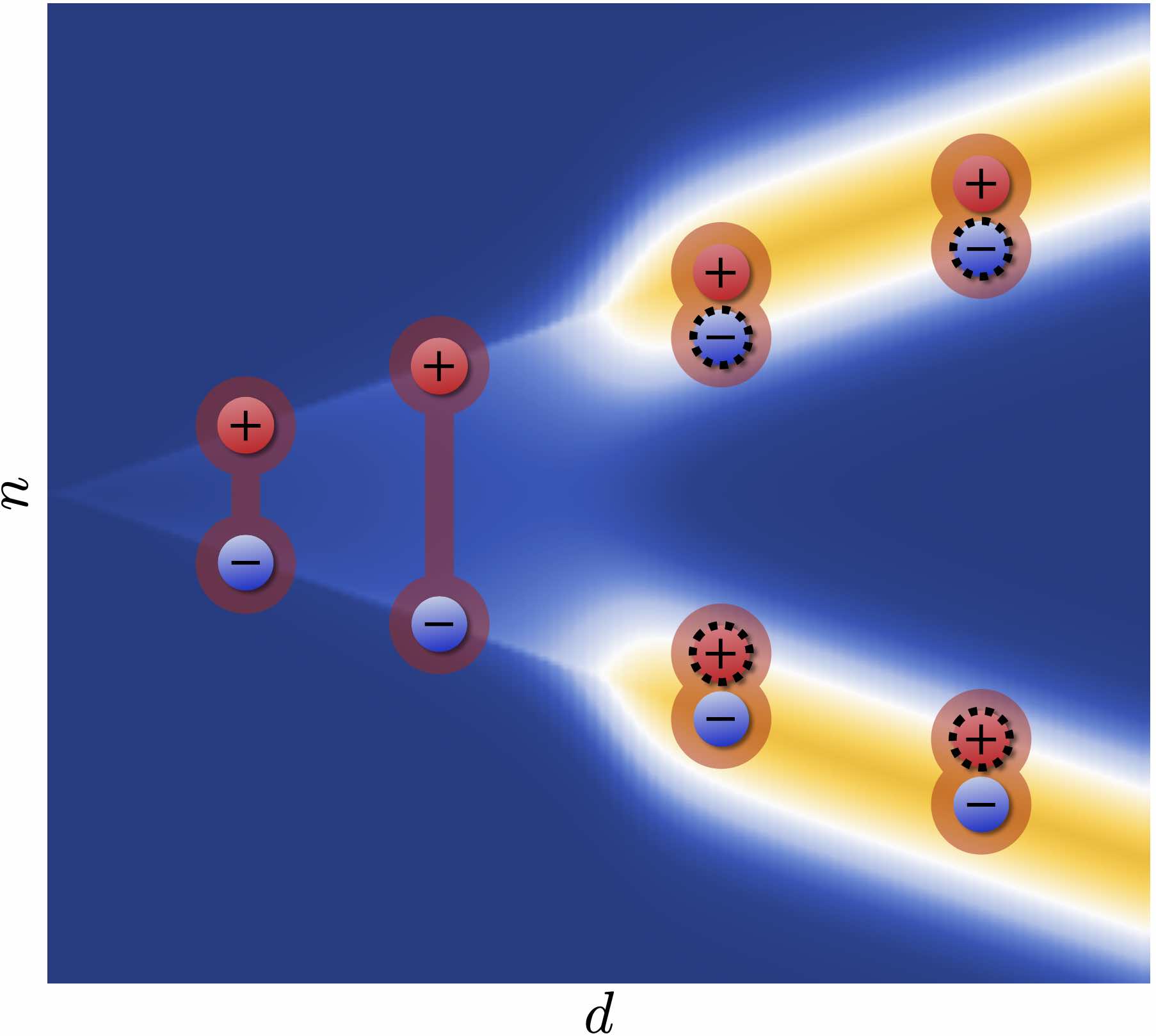
The Quantum Complexity of String Breaking in the Schwinger Model
String breaking, the process by which flux tubes fragment into hadronic states, is a hallmark of confinement in strongly-interacting quantum field theories. We examine a suite of quantum complexity measures using Matrix Product States to dissect the string breaking process in the 1+1D Schwinger model. We demonstrate the presence of nonlocal quantum correlations along the string that may affect fragmentation dynamics, and show that entanglement and magic offer complementary perspectives on string formation and hadronization beyond conventional observables.
We would like to thank Roland Farrell, Henry Froland, Tobias Haug, Dima Kharzeev, Eliana Marroquin and
Caroline Robin for helpful discussions. This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. Sebastian was supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, Grants No. DE-FG02-97ER-41014 and in part by a Feodor Lynen Research fellowship of the Alexander von Humboldt foundation. This work was also supported, in part, by the Department of Physics and the College of Arts and Sciences at the University of Washington. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0032083. This research was done using services provided by the OSG Consortium, which is supported by the National Science Foundation awards #2030508 and #1836650. We have made use of the ITensor library for tensor network computations.
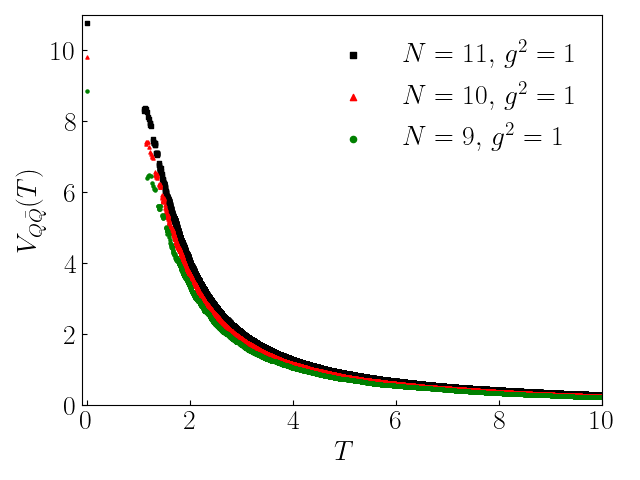
Minimally Truncated SU(3) Lattice Gauge Theory and String Tension
We study SU(3) gauge theory on small lattices in the minimal (qutrit) electric field truncation retaining only the 1, 3, 3bar representations for the link variables. Explicit expressions are given for the Kogut-Susskind Hamiltonian for the square plaquette chain and the two-dimensional honeycomb lattice. Our formalism can be easily extended to the minimally truncated general SU(Nc) gauge theory. The addition of (static) quarks is discussed. We present results for the energy spectrum of the gauge field on these lattices by exact diagonalization of the Hamiltonian and analyze its statistical properties. We also compute the SU(3) string tension and discuss how it is modified by vacuum fluctuations. Finally, we calculate the potential energies of a static quark-antiquark pair and three static quarks and study their screening at finite temperature.
Simulating Fully Gauge-Fixed SU(2) Hamiltonian Dynamics on Digital Quantum Computers
Quantum simulations of many-body systems offer novel methods for probing the dynamics of the Standard Model and its constituent gauge theories. Extracting low-energy predictions from such simulations rely on formulating systematically-improvable representations of lattice gauge theory Hamiltonians that are efficient at all values of the gauge coupling. One such candidate representation for SU(2) is the fully gauge-fixed Hamiltonian defined in the mixed basis. This work focuses on the quantum simulation of the smallest non-trivial system: two plaquettes with open boundary conditions. A mapping of the continuous gauge field degrees of freedom to qubit-based representations is developed. It is found that as few as three qubits per plaquette is sufficient to reach percent-level precision on predictions for observables. Two distinct algorithms for implementing time evolution in the mixed basis are developed and analyzed in terms of quantum resource estimates. One algorithm has favorable scaling in circuit depth for large numbers of qubits, while the other is more practical when qubit count is limited. The second algorithm is used in the measurement of a real-time observable on IBM’s Heron superconducting quantum processor, ibm_fez. The quantum results match classical predictions at the per-mille level. This work lays out the path forward for two- and three-dimensional simulations of larger systems, as well as demonstrating the viability of mixed-basis formulations for studying the properties of SU(2) gauge theories at all values of the gauge coupling.
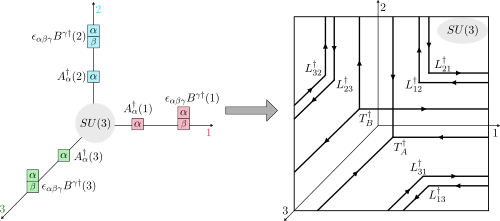
Loop-string-hadron approach to SU(3) lattice Yang-Mills theory, II: Operator representation for the trivalent vertex
This work is the second installment of a series on the Loop-String-Hadron (LSH) approach to SU(3) lattice Yang-Mills theory. Here, we present the infinite-dimensional matrix representation for arbitrary gauge-invariant operators at a trivalent vertex, which results in a standalone framework for computations that supersedes the underlying Schwinger-boson framework. To that end, we evaluate in closed form the result of applying any gauge-invariant operators on the LSH basis states introduced in Part I. Classical calculations in the LSH basis run significantly faster than equivalent calculations performed using Schwinger bosons. A companion code script is provided, which implements the derived formulas and aims to facilitate rapid progress towards Hamiltonian-based calculations of quantum chromodynamics.
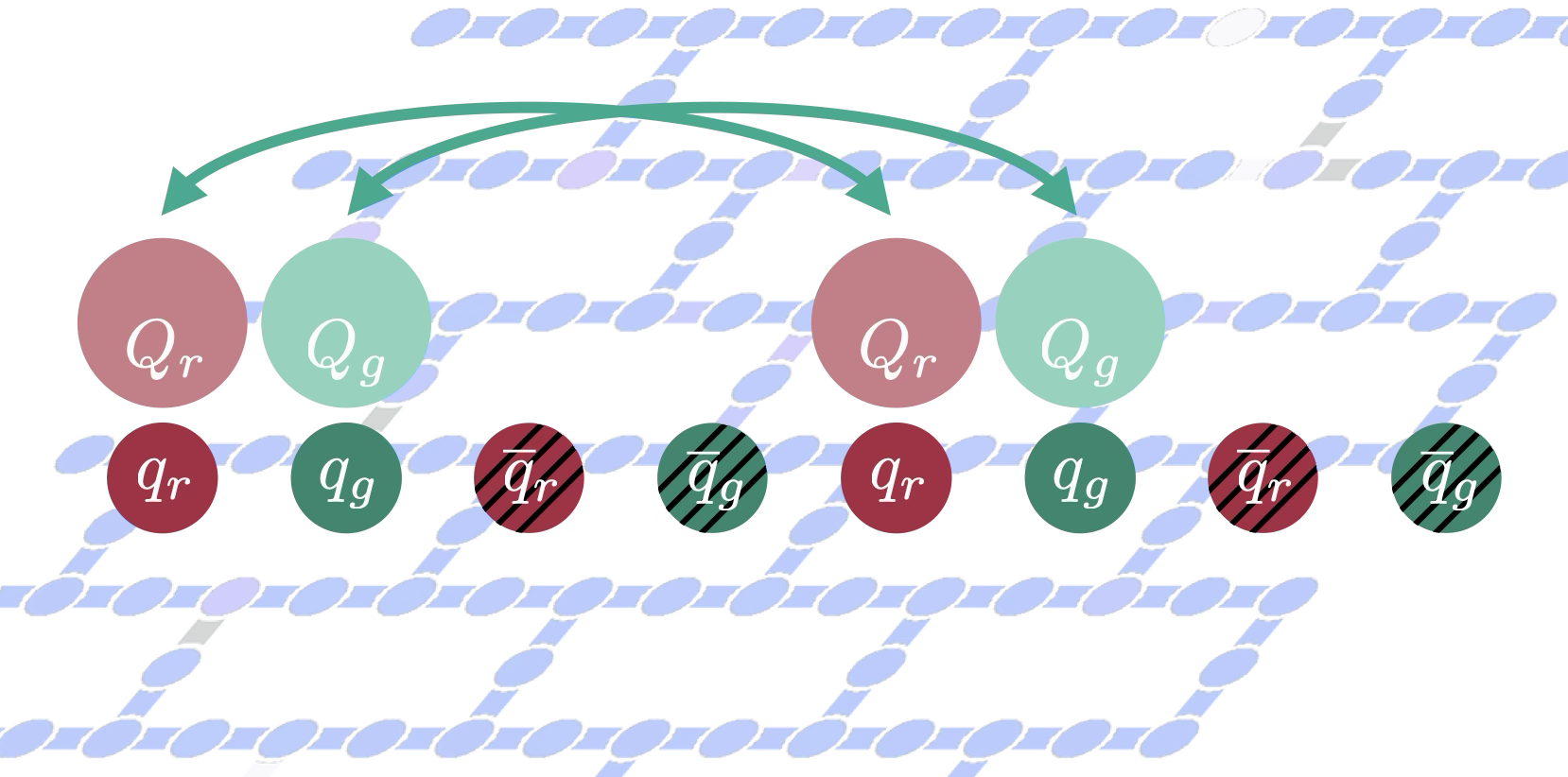
A Framework for Quantum Simulations of Energy-Loss and Hadronization in Non-Abelian Gauge Theories: SU(2) Lattice Gauge Theory in 1+1D
Simulations of energy loss and hadronization are essential for understanding a range of phenomena in non-equilibrium strongly-interacting matter. We establish a framework for performing such simulations on a quantum computer and apply it to a heavy quark moving across a modest-sized 1+1D SU(2) lattice of light quarks. Conceptual advances with regard to simulations of non-Abelian versus Abelian theories are developed, allowing for the evolution of the energy in light quarks, of their local non-Abelian charge densities, and of their multi-partite entanglement to be computed. The non-trivial action of non-Abelian charge operators on arbitrary states suggests mapping the heavy quarks to qubits alongside the light quarks, and limits the heavy-quark motion to discrete steps among spatial lattice sites. Further, the color entanglement among the heavy quarks and light quarks is most simply implemented using hadronic operators, and Domain Decomposition is shown to be effective in quantum state preparation. Scalable quantum circuits that account for the heterogeneity of non-Abelian charge sectors across the lattice are used to prepare the interacting ground-state wavefunction in the presence of heavy quarks. The discrete motion of heavy quarks between adjacent spatial sites is implemented using fermionic SWAP operations. Quantum simulations of the dynamics of a system on L=3 spatial sites are performed using IBM’s ibm_pittsburgh quantum computer using 18 qubits, for which the circuits for state preparation, motion, and one second-order Trotter step of time evolution have a two-qubit depth of 398 after transpilation. A suite of error mitigation techniques are used to extract the observables from the simulations, providing results that are in good agreement with classical simulations. The framework presented here generalizes straightforwardly to other non-Abelian groups, including SU(3) for quantum chromodynamics.
We would like to thank Roland Farrell, Henry Froland and Nikita Zemlevskiy for helpful discussions. This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science, by the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S Department of Energy, and by PNNL’s Quantum Algorithms and Architecture for Domain Science (QuAADS) Laboratory Directed Research and Development (LDRD) Initiative. The Pacific Northwest National Laboratory is operated by Battelle for the U.S. Department of Energy under Contract DE-AC05 76RL01830. It was also supported, in part, by the Department of Physics and the College of Arts and Sciences at the University of Washington. This research used resources of the Oak Ridge Leadership Computing Facility (OLCF), which is a DOE Office of Science User Facility supported under Contract DE AC05-00OR22725. We acknowledge the use of IBM Quantum services for this work. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. We have made extensive use of Wolfram Mathematica, python, julia, jupyter notebooks in the Conda environment, and IBM’s quantum programming environment qiskit. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0032083.

Quantum Error Correction Codes for Truncated SU(2) Lattice Gauge Theories
We construct two quantum error correction codes for pure SU(2) lattice gauge theory in the electric basis truncated at the electric flux $j_{\rm max}=1/2$, which are applicable on quasi-1D plaquette chains, 2D honeycomb and 3D triamond and hyperhoneycomb lattices. The first code converts Gauss’s law at each vertex into a stabilizer while the second only uses half vertices and is locally the carbon code. Both codes are able to correct single-qubit errors. The electric and magnetic terms in the SU(2) Hamiltonian are expressed in terms of logical gates in both codes. The logical-gate Hamiltonian in the first code exactly matches the spin Hamiltonian for gauge singlet states found in previous work.
We would like to thank Alessandro Roggero for use- ful discussions. We acknowledge the workshop “Co- design for Fundamental Physics in the Fault-Tolerant Era” held at the InQubator for Quantum Simulation (IQuS)3 hosted by the Institute for Nuclear Theory in April 2025. This work is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, IQuS under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science
Tensor network simulations of quasi-GPDs in the massive Schwinger model
Generalized Parton Distribution functions (GPDs) are light-cone matrix elements that encode the internal structure of hadrons in terms of quark and gluon degrees of freedom. In this work, we present the first nonperturbative study of quasi-GPDs in the massive Schwinger model, quantum electrodynamics in 1+1 dimensions (QED2), within the Hamiltonian formulation of lattice field theory. Quasi-distributions are spatial correlation functions of boosted states, which approach the relevant light-cone distributions in the luminal limit. Using tensor networks, we prepare the first excited state in the strongly coupled regime and boost it to finite momentum on lattices of up to 400 lattice sites.
We compute both quasiparton distribution functions and, for the first time, quasi-GPDs, and study how they converge with increasing boost and in the continuum limit. In addition, we perform analytic calculations of GPDs in the two-particle Fock-space approximation and in the Reggeized limit, providing qualitative benchmarks for the tensor network results. Our analysis establishes computational benchmarks for accessing partonic observables in low-dimensional gauge theories, offering a starting point for future extensions to higher dimensions, non-Abelian theories, and quantum simulations.
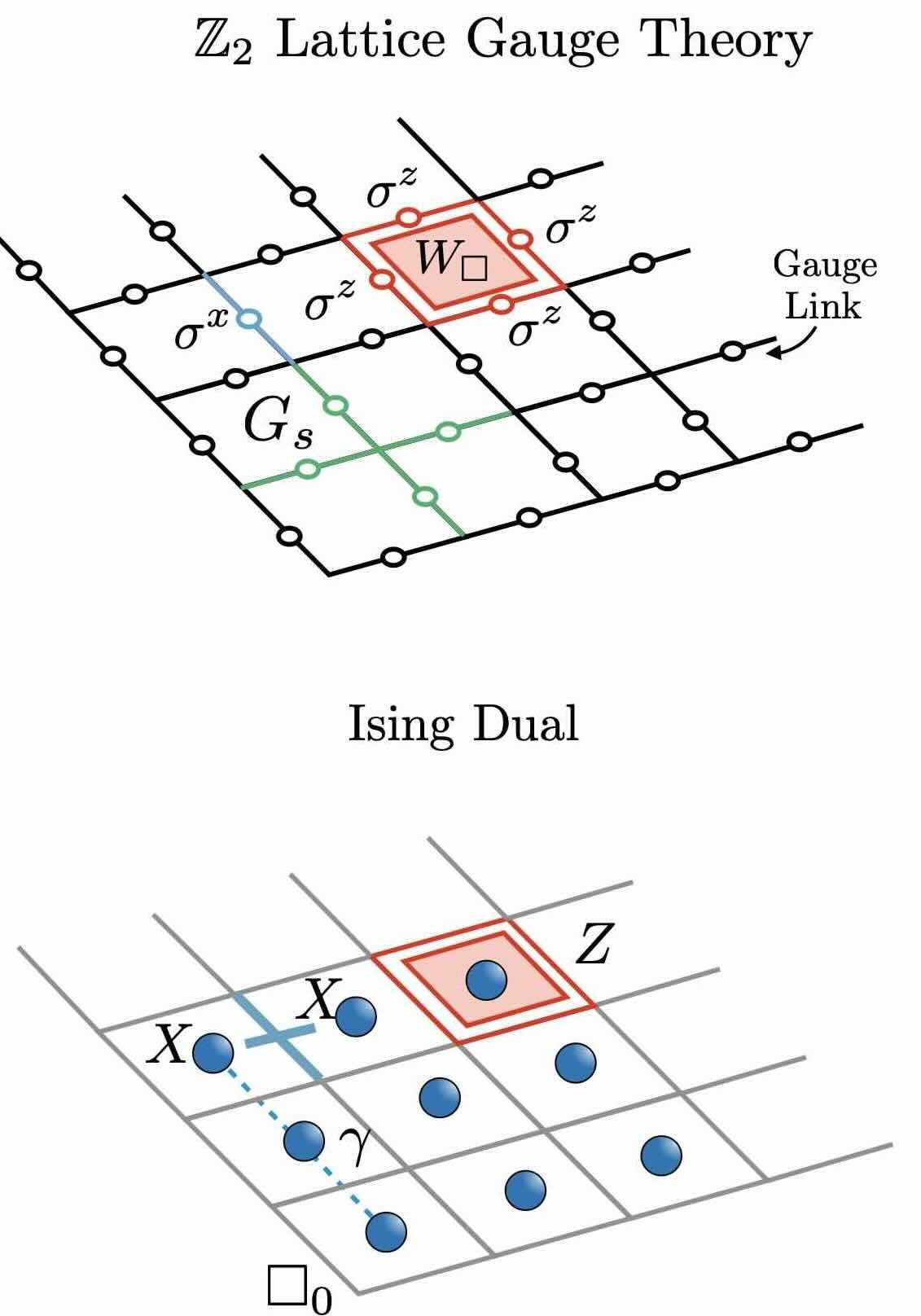
Classical shadows for sample-efficient measurements of gauge-invariant observables
Classical shadows provide a versatile framework for estimating many properties of quantum states from repeated, randomly chosen measurements without requiring full quantum state tomography. When prior information is available—such as knowledge of symmetries of states and operators—this knowledge can be exploited to significantly improve sample efficiency. In this work, we develop three classical shadow protocols tailored to systems with local (or gauge) symmetries to enable efficient prediction of gauge-invariant observables in lattice gauge theory models which are currently at the forefront of quantum simulation efforts. For such models, our approaches can offer exponential improvements in sample complexity over symmetry-agnostic methods, albeit at the cost of increased circuit complexity. We demonstrate these trade-offs using a Z2 lattice gauge theory, where a dual formulation enables a rigorous analysis of resource requirements, including both circuit depth and sample complexity.
We thank Hong-Ye Hu, Jonathan Kunjummen, Martin Larocca, and Yigit Subasi for helpful discussions. J.B. thanks the Harvard Quantum Initiative for support. N.M. (during early stages) and H.F. acknowledge funding by the DOE, Office of Science, Office of Nuclear Physics, IQuS (https://iqus.uw. edu), via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science under Award DE-SC0020970. J.B. notes that the views expressed in this work are those of the author and do not reflect the official policy or position of the U.S. Naval Academy, Department of the Navy, the Department of Defense, or the U.S. Government.
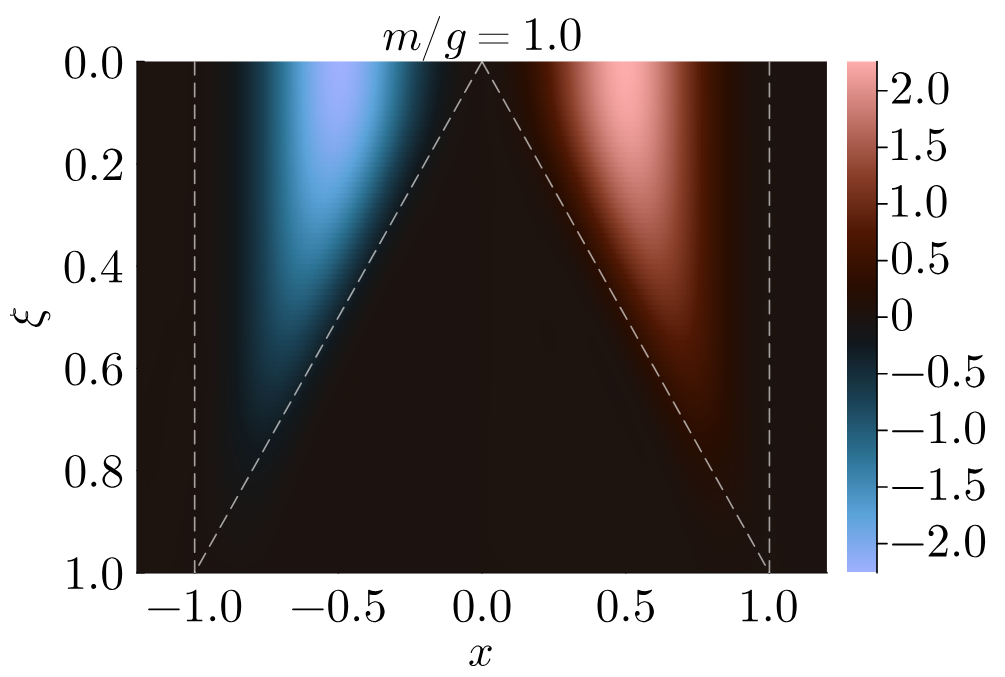
Thermal nature of confining strings
We investigate the quantum statistical properties of the confining string connecting a static fermion-antifermion pair in the massive Schwinger model. By analyzing the reduced density matrix of the subsystem located in between the fermion and antifermion, we demonstrate that as the interfermion separation approaches the string-breaking distance, the overlap between the microscopic density matrix and an effective thermal density matrix exhibits a pronounced, narrow peak, approaching unity at the onset of string breaking. This behavior reveals that the confining flux tube evolves toward a genuinely thermal state as the separation between the charges grows, even in the absence of an external heat bath.
In other words, one cannot tell whether a reduced state of the subsystem arises from a surrounding heat bath or from entanglement with the rest of the system. The entanglement spectrum near the critical string-breaking distance exhibits a rapid transition from the dominance of a single state describing the confining electric string towards a strongly entangled state containing virtual fermion-antifermion pairs.
Our findings establish a quantitative link between confinement, entanglement, and emergent thermality, and suggest that string breaking corresponds to a microscopic thermalization transition within the flux tube.
We are grateful to Adrien Florio, David Frenklakh and Shuzhe Shi for useful discussions and collaboration on related work. We also thank the participants of the QuantHep2025 workshop at Lawrence Berkeley National Lab for insightful comments. This work was supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, Grants No. DE-SC0020970 (InQubator for Quantum Simulation (IQuS), S.G.), DE-FG02-97ER- 41014 (UW Nuclear Theory, S.G.), DE-FG88ER41450 (SBU Nuclear Theory, D.K., E.M.) and by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Co-design Center for Quantum Advantage (C2QA) under Contract No.DE-SC0012704 (S.G., D.K., E.M.). S.G. was supported in part by a Feodor Lynen Research fellowship of the Alexander von Humboldt foundation. E.M. was supported in part by the Center for Distributed Quantum Processing at Stony Brook University.

The Magic Barrier before Thermalization
We investigate the time dependence of anti-flatness in the entanglement spectrum, a measure for non-stabilizerness and lower bound for non-local quantum magic, on a subsystem of a linear SU(2) plaquette chain during thermalization. Tracing the time evolution of a large number of initial states, we find that the anti-flatness exhibits a barrier-like maximum during the time period when the entanglement entropy of the subsystem grows rapidly from the initial value to the microcanonical entropy. The location of the peak is strongly correlated with the time when the entanglement exhibits the strongest growth. This behavior is found for generic highly excited initial computational basis states and persists for coupling constants across the ergodic regime, revealing a universal structure of the entanglement spectrum during thermalization. We conclude that quantitative simulations of thermalization for nonabelian gauge theories require quantum computing. We speculate that this property generalizes to other quantum chaotic systems.
The authors gratefully acknowledge the scientific support and HPC resources provided by the Erlangen National High Performance Computing Center (NHR@FAU) of the Friedrich-Alexander-Universita ̈t Erlangen-Nu ̈rnberg(FAU).B.M.acknowledgessupport by the U.S. Department of Energy, Office of Science (grant DE-FG02-05ER41367). X.Y. is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science and acknowledges the discussions at the “Many-Body Quantum Magic” workshop held at the IQuS hosted by the Institute for Nuclear Theory in Spring 2025. L.E. acknowledges funding by the Max Planck Society, the Deutsche Forschungsgemein- schaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2111 – 390814868, and the European Research Council (ERC) under the European Union’s Horizon Europe research and innovation program (Grant Agreement No. 101165667)—ERC Starting Grant QuSiGauge. Views and opinions expressed are those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. This work is part of the Quantum Computing for High-Energy Physics (QC4HEP) working group. C.S. would like to thank the organizers and participants of the QuantHEP 2025 conference at Lawrence Berkeley National Lab for valuable discussions that contributed to this work.

Anti-Flatness and Non-Local Magic in Two-Particle Scattering Processes
Non-local magic and anti-flatness provide a measure of the quantum complexity in the wavefunction of a physical system. Supported by entanglement, they cannot be removed by local unitary operations, thus providing basis-independent measures, and sufficiently large values underpin the need for quantum computers in order to perform precise simulations of the system at scale. Towards a better understanding of the quantum-complexity generation by fundamental interactions, the building blocks of many-body systems, we consider non-local magic and anti-flatness in two-particle scattering processes, specifically focusing on low-energy nucleon-nucleon scattering and high-energy Moller scattering. We find that the non-local magic induced in both interactions is four times the anti-flatness (which is found to be true for any two-qubit wavefunction), and verify the relation between the Clifford-averaged anti-flatness and total magic. For these processes, the anti-flatness is a more experimentally accessible quantity as it can be determined from one of the final-state particles, and does not require spin correlations. While the MOLLER experiment at the Thomas Jefferson National Accelerator Facility does not include final-state spin measurements, the results presented here may add motivation to consider their future inclusion.
We would like to thank Krishna Kumar for enlightening discussions about MOLLER and other electron scattering experiments. We are grateful to the organizers and participants of the First and Second International Workshops on Many-Body Quantum Magic. This work was supported, in part, by Universitat Bielefeld (Caroline), and by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Martin). This work was also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington. We have made extensive use of Wolfram Mathematica.

Theory of quarkonia as probes for deconfinement
This is a plenary talk given at Quark Matter 2025, summarizing recent theoretical developments for the understanding of quarkonium production in relativistic heavy ion collisions and how quarkonium uniquely probes the deconfined phase of QCD matter.

Eigenstate Thermalization in 1+1-Dimensional SU(2) Lattice Gauge Theory Coupled with Dynamical Fermions
We test the eigenstate thermalization hypothesis (ETH) in 1+1-dimensional SU(2) lattice gauge theory (LGT) with one flavor of dynamical fermions. Using the loop-string-hadron framework of the LGT with a bosonic cut-off, we exactly diagonalize the Hamiltonian for finite size systems and calculate matrix elements (MEs) in the eigenbasis for both local and non-local operators. We analyze different indicators to identify the parameter space for quantum chaos at finite lattice sizes and investigate how the ETH behavior emerges in both the diagonal and off-diagonal MEs. Our investigations allow us to study various time scales of thermalization and the emergence of random matrix behavior, and highlight the interplays of the several diagnostics with each other. Furthermore, from the off-diagonal MEs, we extract a smooth function that is closely related to the spectral function for both local and non-local operators. We find numerical evidence of the spectral gap and the memory peak in the non-local operator case. Finally, we investigate aspects of subsystem ETH in the lattice gauge theory and find some features in the subsystem reduced density matrix that are unique to gauge theories.

Observation of quantum-field-theory dynamics on a spin-phonon quantum computer
Simulating out-of-equilibrium dynamics of quantum field theories in nature is challenging with classical methods, but is a promising application for quantum computers. Unfortunately, simulating interacting bosonic fields involves a high boson-to-qubit encoding overhead. Furthermore, when mapping to qubits, the infinite-dimensional Hilbert space of bosons is necessarily truncated, with truncation errors that grow with energy and time. A qubit-based quantum computer, augmented with an active bosonic register, and with qubit, bosonic, and mixed qubit-boson quantum gates, offers a more powerful platform for simulating bosonic theories. We demonstrate this capability experimentally in a hybrid analog-digital trapped-ion quantum computer, where qubits are encoded in the internal states of the ions, and the bosons in the ions’ motional states. Specifically, we simulate nonequilibrium dynamics of a (1+1)-dimensional Yukawa model, a simplified model of interacting nucleons and pions, and measure fermion- and boson-occupation-state probabilities. These dynamics populate high bosonic-field excitations starting from an empty state, and the experimental results capture well such high-occupation states. This simulation approaches the regime where classical methods become challenging, bypasses the need for a large qubit overhead, and removes truncation errors. Our results, therefore, open the way to achieving demonstrable quantum advantage in qubit-boson quantum computing.

On Quantum Simulation of QED in Coulomb Gauge
A recent work (Li, 2406.01204) considered quantum simulation of Quantum Electrodynamics (QED) on a lattice in the Coulomb gauge with gauge degrees of freedom represented in the occupation basis in momentum space. Here we consider representing the gauge degrees of freedom in field basis in position space and develop a quantum algorithm for real-time simulation. We show that the Coulomb gauge Hamiltonian is equivalent to the temporal gauge Hamiltonian when acting on physical states consisting of fermion and transverse gauge fields. The Coulomb gauge Hamiltonian guarantees that the unphysical longitudinal gauge fields do not propagate and thus there is no need to impose any constraint. The local gauge field basis and the canonically conjugate variable basis are swapped efficiently using the quantum Fourier transform. We prove that the qubit cost to represent physical states and the gate depth for real-time simulation scale polynomially with the lattice size, energy, time, accuracy and Hamiltonian parameters. We focus on the lattice theory without discussing the continuum limit or the UV completion of QED.
Parton Distributions on a Quantum Computer
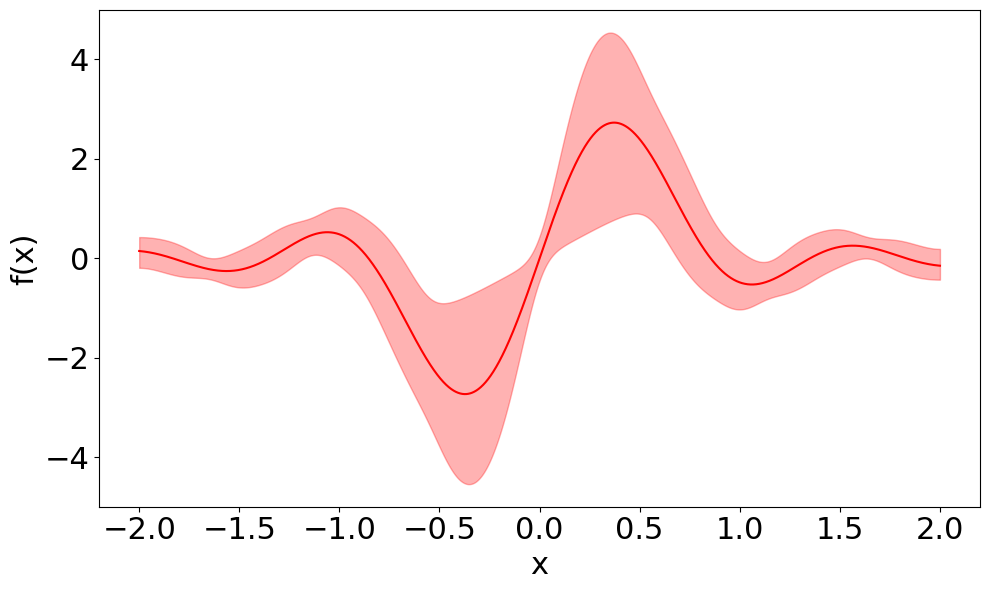
We perform the first quantum computation of parton distribution function (PDF) with a real quantum device by calculating the PDF of the lightest positronium in the Schwinger model with IBM quantum computers. The calculation uses 10 qubits for staggered fermions at five spatial sites and one ancillary qubit. The most critical and challenging step is to reduce the number of two-qubit gate depths to around 500 so that sensible results start to emerge. The resulting lightcone correlators have excellent agreement with the classical simulator result in central values, although the error is still large. Compared with classical approaches, quantum computation has the advantage of not being limited in the accessible range of parton momentum fraction x due to renormalon ambiguity, and the difficulty of accessing non-valence partons. A PDF calculation with 3+1 dimensional QCD near x=0 or x=1 will be a clear demonstration of the quantum advantage on a problem with great scientific impact.
Non-Abelian Dynamics on a Cube: Improving Quantum Compilation through Qudit-Based Simulations
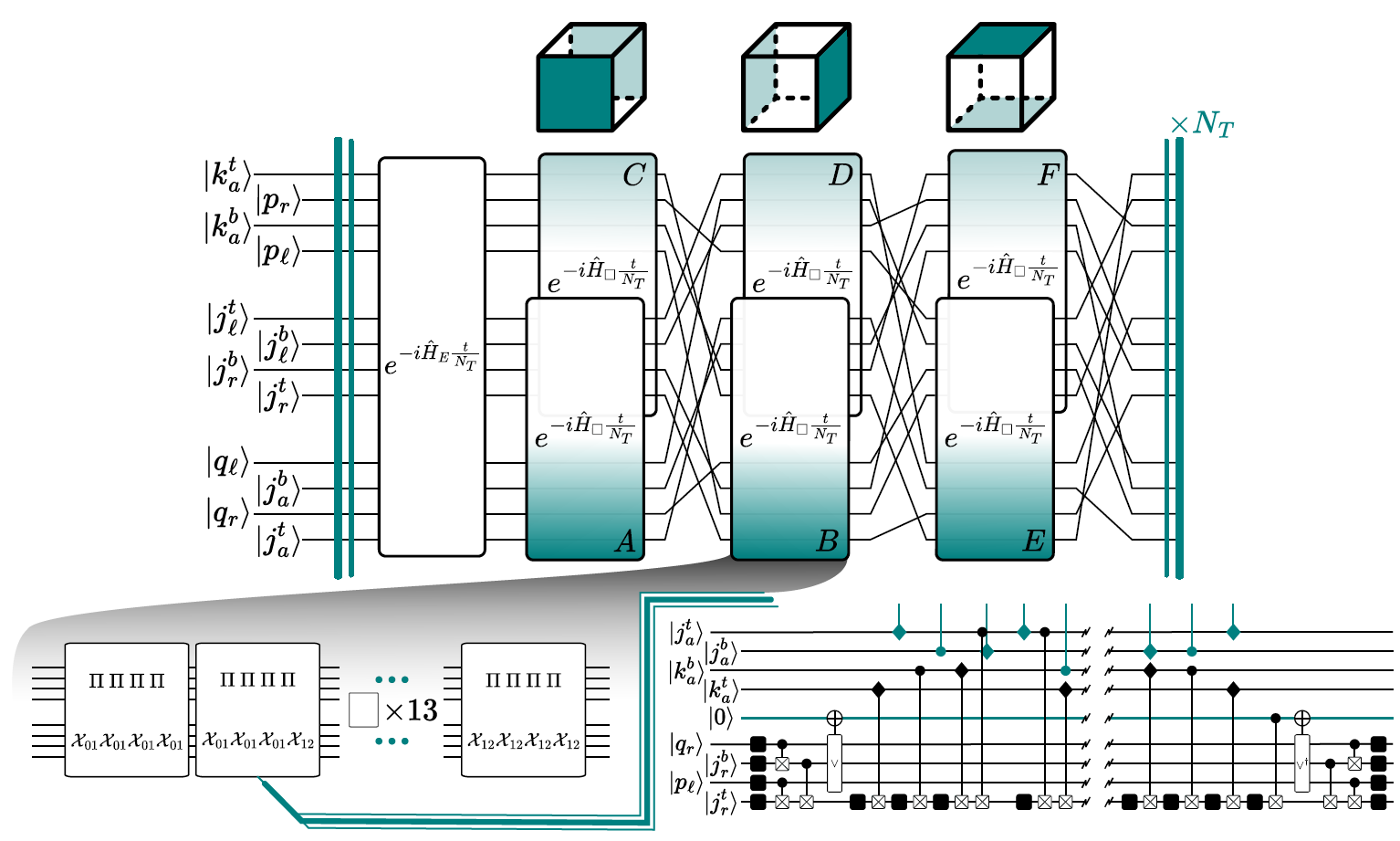
Recent developments in mapping lattice gauge theories relevant to the Standard Model onto digital quantum computers identify scalable paths with well-defined quantum compilation challenges toward the continuum. As an entry point to these challenges, we address the simulation of SU(2) lattice gauge theory. Using qudit registers to encode the digitized gauge field, we provide quantum resource estimates, in terms of elementary qudit gates, for arbitrarily high local gauge field truncations. We then demonstrate an end-to-end simulation of real-time, qutrit-digitized SU(2) dynamics on a cube. Through optimizing the simulation, we improved circuit decompositions for uniformly-controlled qudit rotations, an algorithmic primitive for general applications of quantum computing. The decompositions also apply to mixed-dimensional qudit systems, which we found advantageous for compiling lattice gauge theory simulations. Furthermore, we parallelize the evolution of opposite faces in anticipation of similar opportunities arising in three-dimensional lattice volumes. This work details an ambitious executable for future qudit hardware and attests to the value of codesign strategies between lattice gauge theory simulation and quantum compilation.
This collaboration was funded by the NSERC Alliance International Catalyst Quantum Grant program (ALLRP 586483-23). JJ is funded in part by the NSERC CREATE in Quantum Computing Program, grant number 543245. NK acknowledges funding in part from the NSF STAQ Program (PHY-1818914). ODM acknowledges funding from NSERC, the Canada Research Chairs Program, and UBC. This work was conceived at the 2023 Quantum Computing, Quantum Simulation, Quan- tum Gravity and the Standard Model workshop at the InQubator for Quantum Simulation (IQuS) hosted by the Institute for Nuclear Theory (INT). IQuS is supported by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science, and by the Department of Physics, and the College of Arts and Sciences at the University of Washington.
Pathfinding Quantum Simulations of Neutrinoless Double-Beta Decay
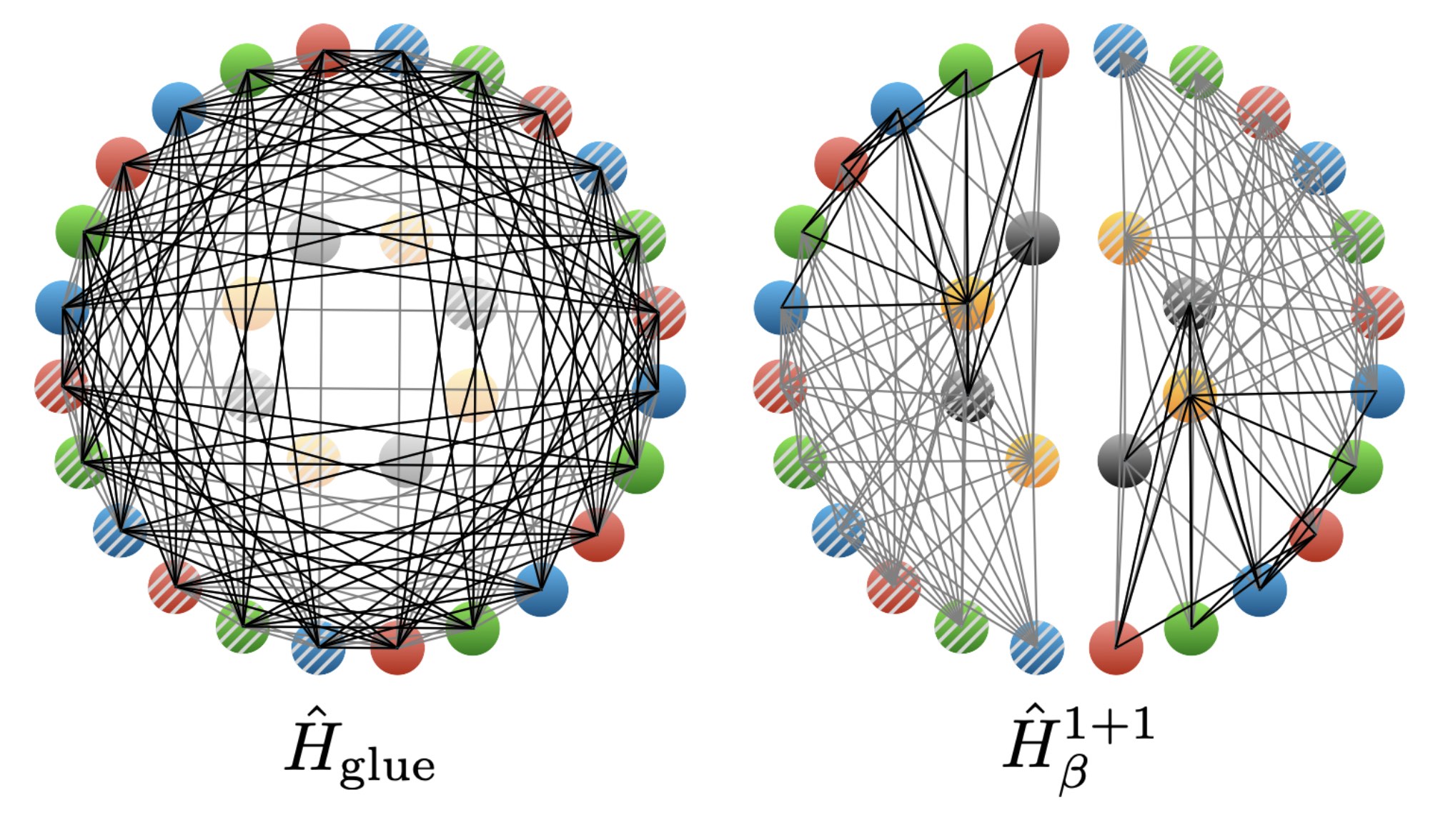
We present results from co-designed quantum simulations of the neutrinoless double-beta decay of a two-hadron nucleus in 1+1D quantum chromodynamics using IonQ’s Forte-generation trapped-ion quantum computers. Two flavors of dynamical quarks and leptons are distributed across two lattice sites and mapped to 32 qubits. An effective four-Fermi contact interaction is used to implement charged-current weak interactions between quarks and leptons, and lepton-number violation is induced by a neutrino Majorana mass. Statistically-significant signals for the neutrinoless decay of a two-hadron nucleus are measured during time evolution with a non-zero Majorana mass, making this the first quantum simulation to observe lepton-number violation in real time. This was made possible by co-designing the state preparation and time evolution quantum circuits to maximally utilize the all-to-all connectivity and native gate-set available on IonQ’s quantum computers. Quantum circuit compilation techniques and symmetry-aware error-mitigation methods, tailored to neutrinoless decays, allow accurate results to be extracted from quantum circuits with up to 470 two-qubit gates using Forte Enterprise. We present first benchmarks toward the real-time simulation of neutrinoless double-beta decay, and discuss the potential of future quantum simulations to provide yocto-second resolution of the reaction pathway for nuclear processes.
We would like to thank Saurabh Kadam for helpful discussions. This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (MJS, IC, RCF), and by the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (MI, IC). This work is also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington. RCF acknowledges support from the U.S. Department of Energy QuantISED program through the theory consortium “Intersections of QIS and Theoretical Particle Physics” at Fermilab, from the U.S. Department of Energy, Office of Science, Accelerated Research in Quantum Computing, Quantum Utility through Advanced Computational Quantum Algorithms (QUACQ), and from the Institute for Quantum Information and Matter, an NSF Physics Frontiers Center (PHY-2317110). RCF additionally acknowledges support from a Burke Institute prize fellowship. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0032083. AM, FT, MALR, AA, YDS, AB, CG, AK and MR are employees and equity holders of IonQ, Inc.
Quantum computation of hadron scattering in a lattice gauge theory
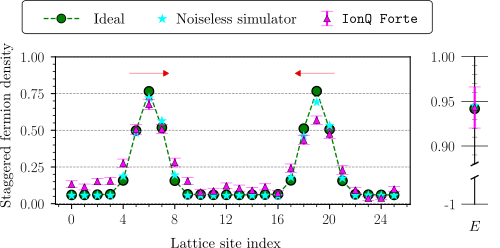
We present a digital quantum computation of two-hadron scattering in a Z2 lattice gauge theory in 1+1 dimensions. We prepare well-separated single-particle wave packets with desired momentum-space wavefunctions, and simulate their collision through digitized time evolution. Multiple hadronic wave packets can be produced using the systematically improvable algorithm of this work, achieving high fidelity with the target initial state, and demanding only polynomial resources in system size. Specifically, employing a trapped-ion quantum computer (IonQ Forte), we prepare up to three meson wave packets\ using 11 and 27 system qubits, and simulate collision dynamics of two meson wave packets for the smaller system. Despite noise effects, post-processing with a global-symmetry-based noise mitigation yields results consistent with numerical simulations, but decoherence limits evolution into long times. We demonstrate the critical role of high-fidelity initial states for precision measurements of state-sensitive observables, such as S-matrix elements and decay amplitudes. While we have not established quantum advantage by this early hardware demonstration, our algorithms are general, and our findings imply the potential of quantum computers in simulating scattering processes in strongly interacting gauge theories.
Quantum-emulator and quantum-hardware computations of this work were enabled by access to IonQ systems provided by the University of Maryland’s National Quantum Laboratory (QLab). We thank support from IonQ scientists and engineers, especially Daiwei Zhu, during the execution of our runs. We further thank Franz Klein at QLab for the help in setting up access and communications with IonQ contacts. S.K. acknowledges valuable discussions with Roland Farrell and Francesco Turro. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. The numerical results in this work were obtained using Qiskit [204], ITensors [205], Julia [206] and Jupyter Notebook [207] software applications within the Conda [208] environment.
Z.D. and C-C.H. acknowledge support from the National Science Foundation’s Quantum Leap Challenge Institute on Robust Quantum Simulation (award no. OMA-2120757); the U.S. Department of Energy (DOE), Office of Science, Early Career Award (award no. DESC0020271); and the Department of Physics, Maryland Center for Fundamental Physics, and College of Computer, Mathematical, and Natural Sciences at the University of Maryland, College Park. Z.D. is further grateful for the hospitality of Nora Brambilla, and of the Excellence Cluster ORIGINS at the Technical University of Munich, where part of this work was carried out. The research at ORIGINS is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy (EXC-2094—390783311). S.K. acknowledges support by the U.S. DOE, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (award no. DE-SC0020970), and by the DOE QuantISED program through the theory consortium “Intersections of QIS and Theoretical Particle Physics” at Fermilab (Fermilab subcontract no. 666484). This work was also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.

Quarkonia Theory: From Open Quantum System to Classical Transport
This is a theoretical overview of quarkonium production in relativistic heavy ion collisions given for the Hard Probe 2024 conference at Nagasaki. The talk focuses on the application of the open quantum system framework and the formulation of the chromoelectric correlator that uniquely encodes properties of the quark-gluon plasma relevant for quarkonium dynamics and thus can be extracted from theory-experiment comparison.
This work is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science.
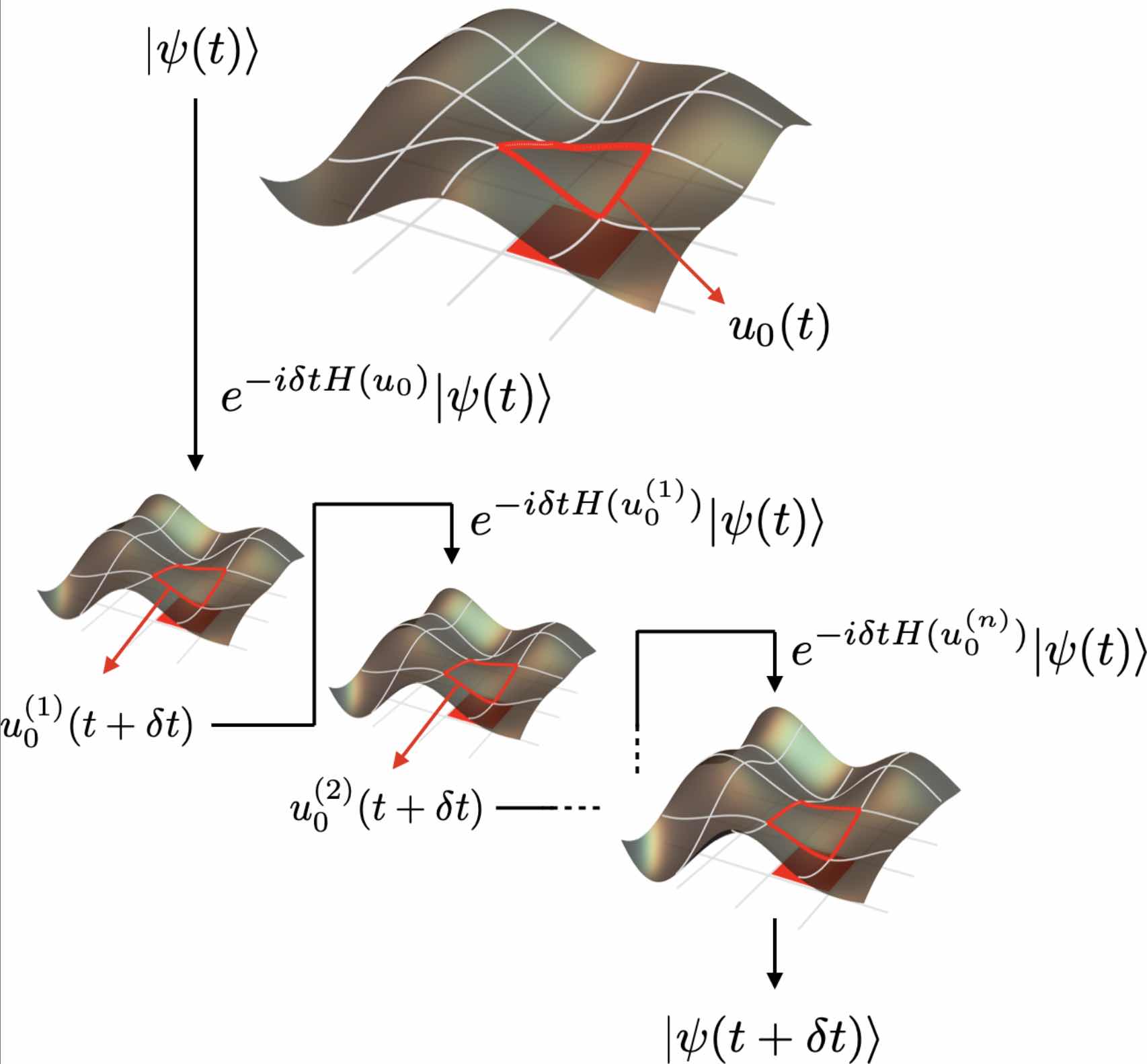
Dynamical Local Tadpole-Improvement in Quantum Simulations of Gauge Theories
We identify a new element in quantum simulations of lattice gauge theories, arising from spacetime-dependent quantum corrections in the relation between the link variables defined on the lattice and their continuum counterparts. While in Euclidean spacetime simulations, based on Monte Carlo sampling, the corresponding tadpole improvement leads to a constant rescaled value per gauge configuration, in Minkowski spacetime simulations it requires a state- and time dependent update of the coefficients of operators involving link variables in the Hamiltonian. To demonstrate this effect, we present the results of numerical simulations of the time evolution of truncated SU(2) plaquette chains and honeycomb lattices in 2+1D, starting from excited states with regions of high energy density, and with and without entanglement.
We would like to thank Randy Lewis for helpful discussions regarding the classical implementation of tadpole improvement. This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Martin, Xiaojun), and by the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (Marc). This work is also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington. We have made extensive use of Wolfram Mathematica. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0032083.
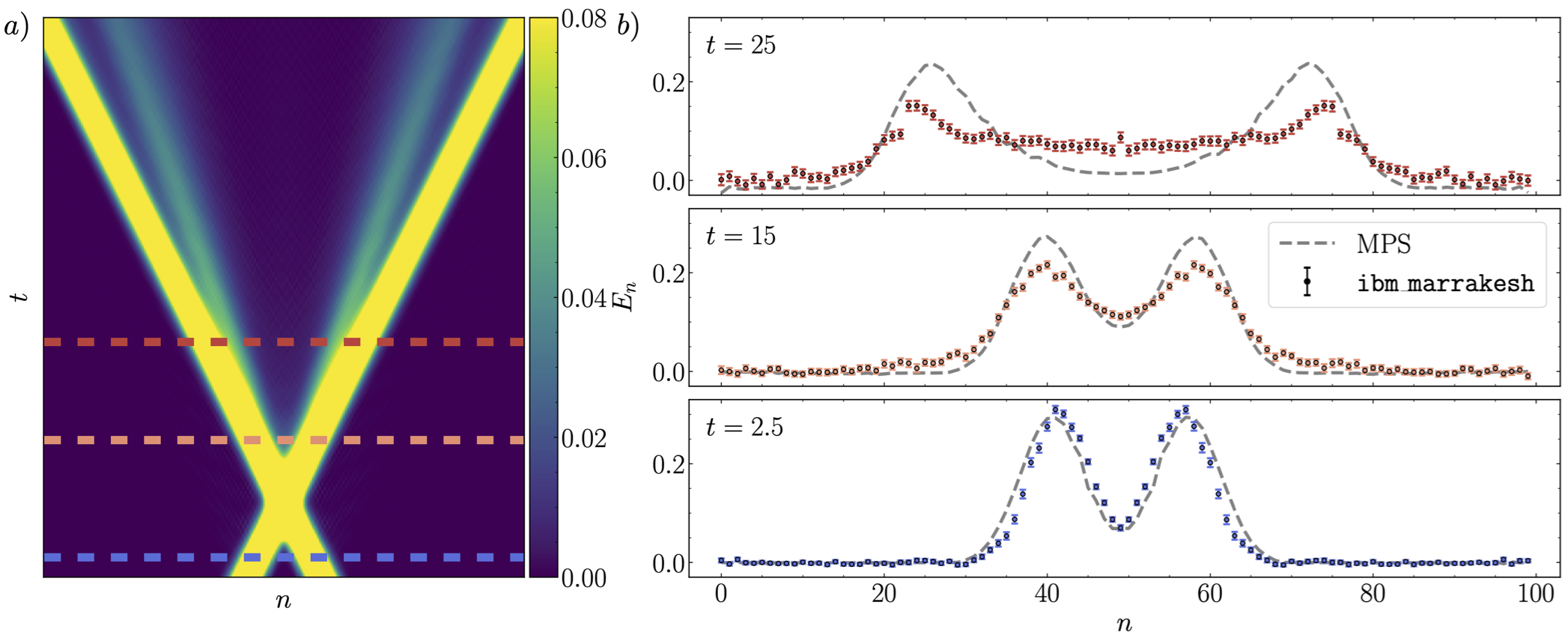
Digital Quantum simulations of particle collisions in quantum field theories using W states
A new quantum algorithm for preparing the initial state (wavepackets) of a quantum field theory scattering simulation is introduced. This method extends recent techniques for preparing W states using mid-circuit measurement and feedforward to efficiently create wavepackets. The required circuit depth is independent of wavepacket size, representing a superexponential improvement over previous methods. Explicit examples are provided for one-dimensional Ising field theory, scalar field theory, the Schwinger model, and two dimensional Ising field theory. The circuits that prepare wavepackets in one-dimensional Ising field theory are used to simulate scattering on 100 qubits of IBM’s quantum computer ibm_marrakesh. Quantum simulations are performed at a center of mass energy above inelastic threshold, and measurements of the energy density in the post-collision state reveal the production of new particles. A novel error mitigation strategy based on energy conservation enables accurate results to be extracted from circuits with up to 6,412 two-qubit gates. The prospects for a near-term quantum advantage in simulations of scattering are discussed.
We would like to thank Ivan Chernyshev, David Simmons-Duffin, Johnnie Gray, Ash Milsted, Martin Sav- age and Federica Surace for helpful discussions. RF and JP acknowledge support from the U.S. Department of Energy QuantISED program through the theory consortium “Intersections of QIS and Theoretical Particle Physics” at Fermilab, from the U.S. Department of Energy, Office of Science, Accelerated Research in Quantum Computing, Quantum Utility through Advanced Computational Quantum Algorithms (QUACQ), and from the Institute for Quantum Information and Matter, an NSF Physics Frontiers Center (PHY-2317110). RF additionally acknowledges support from a Burke Institute prize fellowship. NZ acknowledges support provided by the DOE, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the pro- gram on Quantum Horizons: QIS Research and Innovation for Nuclear Science. NZ is also supported by the Department of Physics and the College of Arts and Sciences at the University of Washington. MI acknowledges support provided by the Quantum Science Center (QSC), which is a National Quantum Information Science Research Center of the U.S. Department of Energy. JP acknowledges funding provided by the U.S. Department of Energy Office of High Energy Physics (DE-SC0018407), the U.S. Department of Energy, Office of Science, Accelerated Research in Quantum Computing, Fundamental Algorithmic Research toward Quantum Utility (FAR- Qu), and the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Quantum Systems Accelerator. The computations presented in this work were conducted in the Resnick High Performance Computing Center, a facility supported by the Resnick Sustainability Institute at Caltech and also enabled by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. RF and NZ acknowledge the use of IBM Quantum Credits for this work. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team.

Quarkonium suppression in strongly coupled plasmas
Suppression of open heavy quarks and quarkonia in heavy-ion collisions are among the most informative probes of quark-gluon plasma (QGP). Interpreting the full wealth of data obtained from the collision events requires a precise theoretical understanding of the evolution of heavy quarks and quarkonia as they propagate through a strongly coupled plasma. Such calculations require the evaluation of a gauge-invariant correlator of chromoelectric fields. This chromoelectric correlator encodes all the characteristics of QGP that the dissociation and recombination dynamics of quarkonium are sensitive to, which is to say can in principle measure. We review its distinctive qualitative features at weak coupling in QCD up to next-to-leading order and at strong coupling in $\mathcal{N}=4$ SYM using the AdS/CFT correspondence, as well as its formulation in Euclidean QCD. Furthermore, we report on recent progress in applying our results to the calculation of the final quarkonium abundances after propagating through a cooling droplet of QGP, which illustrates how we may learn about QGP from quarkonium measurements. We devote special attention to how the presence of a strongly coupled plasma modifies the transport description of quarkonium, in comparison to approaches that rely on weak coupling approximations to describe quarkonium dissociation and recombination.
The work of BSH is supported by grant NSF PHY-2309135 to the Kavli Institute for Theoretical Physics (KITP), and by grant 994312 from the Simons Foundation. XY is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science.
Quantum Simulations of Fundamental Physics
Simulating the dynamics of non-equilibrium matter under extreme conditions lies beyond the capabilities of classical computation alone. Remarkable advances in quantum information science and technology are profoundly changing how we understand and explore fundamental quantum many-body systems, and have brought us to the point of simulating essential aspects of these systems using quantum computers. I discuss highlights, opportunities and the challenges that lie ahead.
Improved Honeycomb and Hyper-Honeycomb Lattice Hamiltonians for Quantum Simulations of Non-Abelian Gauge Theories
Improved Kogut-Susskind Hamiltonians for quantum simulations of non-Abelian Yang-Mills gauge theories are developed for honeycomb (2+1D) and hyper-honeycomb (3+1D) spatial tessellations. This is motivated by the desire to identify lattices for quantum simulations that involve only 3-link vertices among the gauge field group spaces in order to reduce the complexity in applications of the plaquette operator. For the honeycomb lattice, we derive a classically O(b²)-improved Hamiltonian, with b being the lattice spacing. Tadpole improvement via the mean-field value of the plaquette operator is used to provide the corresponding quantum improvements. We have identified the (non-chiral) hyper-honeycomb as a candidate spatial tessellation for 3+1D quantum simulations of gauge theories, and determined the associated O(b)-improved Hamiltonian.
This work was supported, in part, by the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (Marc), and by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Martin, Xiaojun).

Quarkonium Polarization Kinetic Equation from Open Quantum Systems and Effective Field Theories
Recent measurements of polarization phenomena in relativistic heavy ion collisions have aroused a great interest in understanding dynamical spin evolution of the QCD matter. In particular, the spin alignment signature of $J/\psi$ has been recently observed in Pb-Pb collisions at LHC, which may infer nontrivial spin transport of quarkonia in quark gluon plasmas. Motivated by this, we study the spin-dependent in-medium dynamics of quarkonia by using the potential nonrelativistic QCD (pNRQCD) and the open quantum system framework. By applying the Markovian approximation and Wigner transformation, we systematically derive the Boltzmann transport equation for vector quarkonia with polarization dependence in the quantum optical limit. As opposed to the previous study for the spin-independent case where the collision terms depend on chromoelectric correlators, the new kinetic equation incorporates gauge invariant correlators of chromomagnetic fields that determine the recombination and dissociation terms with polarization dependence at the order we are working in the multipole expansion. In the quantum Brownian motion limit, the Lindblad equation with new transport coefficients defined in terms of the chromomagnetic field correlators have also been derived. Our formalism is generic and valid for both weakly-coupled and strongly-coupled quark gluon plasmas. It may be further applied to study spin alignment of vector quarkonia in heavy ion collisions.

Emergent Hydrodynamic Mode on SU(2) Plaquette Chains and Quantum Simulation
We search for emergent hydrodynamic modes in real-time Hamiltonian dynamics of 2+1-dimensional SU(2) lattice gauge theory on a quasi one dimensional plaquette chain, by numerically computing symmetric correlation functions of energy densities on lattice sizes of about 20 with the local Hilbert space truncated at j_max=1/2 Due to the Umklapp processes, we only find a mode for energy diffusion. The symmetric correlator exhibits transport peak near zero frequency with a width proportional to momentum squared at small momentum, when the system is fully quantum ergodic, as indicated by the eigenenergy level statistics. This transport peak leads to a power-law t^(-1/2) decay of the symmetric correlator at late time, also known as the long-time tail, as well as diffusion-like spreading in position space. We also introduce a quantum algorithm for computing the symmetric correlator on a quantum computer and find it gives results consistent with exact diagonalization when tested on the IBM emulator. Finally we discuss the future prospect of searching for the sound modes.
We thank Anton Andreev, Paul Romatschke and Larry Yaffe for discussions that inspired this study. This work is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP- ERCAP0032083. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington.
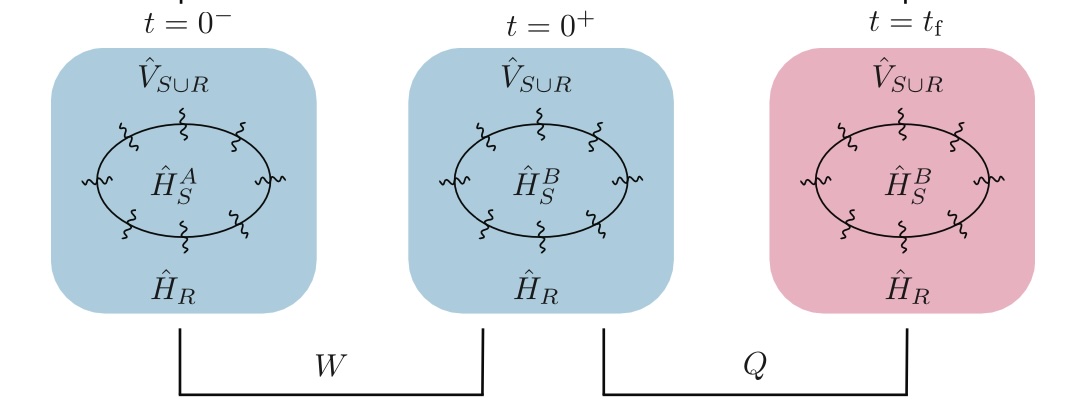
Work and heat exchanged during sudden quenches of strongly coupled quantum systems
How should one define thermodynamic quantities (internal energy, work, heat, etc.) for quantum systems coupled to their environments strongly? We examine three (classically equivalent) definitions of a quantum system’s internal energy under strong-coupling conditions. Each internal-energy definition implies a definition of work and a definition of heat. Our study focuses on quenches, common processes in which the Hamiltonian changes abruptly. In these processes, the first law of thermodynamics holds for each set of definitions by construction. However, we prove that only two sets obey the second law. We illustrate our findings using a simple spin model. Our results guide studies of thermodynamic quantities in strongly coupled quantum systems.
This work was supported by the DOE, Office of Science, Office of Nuclear Physics, IQuS (\url{https://iqus.uw.edu}), via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science under Award DE-SC0020970; and by the National Science Foundation (NSF) Quantum Leap Challenge Institutes (QLCI) (award no.~OMA-2120757); and by the Department of Energy (DOE), Office of Science, Early Career Award (award no.~DESC0020271), as well as by the Department of Physics; Maryland Center for Fundamental Physics; and College of Computer, Mathematical, and Natural Sciences at the University of Maryland, College Park. Part of this work was supported i by the Government of Canada through the Department of Innovation, Science, and Economic Development and by the Province of Ontario through the Ministry of Colleges and Universities; and by the Simons Foundation through the Simons Foundation Emmy Noether Fellows Program at Perimeter InstituteThe work was supported in part by the NSF award PHY-2309135 and by the John Templeton Foundation (award no.~62422).
The Present and Future of QCD
This White Paper presents the community inputs and scientific conclusions from the Hot and Cold QCD Town Meeting that took place September 23-25, 2022 at MIT, as part of the Nuclear Science Advisory Committee (NSAC) 2023 Long Range Planning process. A total of 424 physicists registered for the meeting. The meeting highlighted progress in Quantum Chromodynamics (QCD) nuclear physics since the 2015 LRP (LRP15) and identified key questions and plausible paths to obtaining answers to those questions, defining priorities for our research over the coming decade. In defining the priority of outstanding physics opportunities for the future, both prospects for the short (~ 5 years) and longer term (5-10 years and beyond) are identified together with the facilities, personnel and other resources needed to maximize the discovery potential and maintain United States leadership in QCD physics worldwide. This White Paper is organized as follows: In the Executive Summary, we detail the Recommendations and Initiatives that were presented and discussed at the Town Meeting, and their supporting rationales. Section 2 highlights major progress and accomplishments of the past seven years. It is followed, in Section 3, by an overview of the physics opportunities for the immediate future, and in relation with the next QCD frontier: the EIC. Section 4 provides an overview of the physics motivations and goals associated with the EIC. Section 5 is devoted to the workforce development and support of diversity, equity and inclusion. This is followed by a dedicated section on computing in Section 6. Section 7 describes the national need for nuclear data science and the relevance to QCD research.
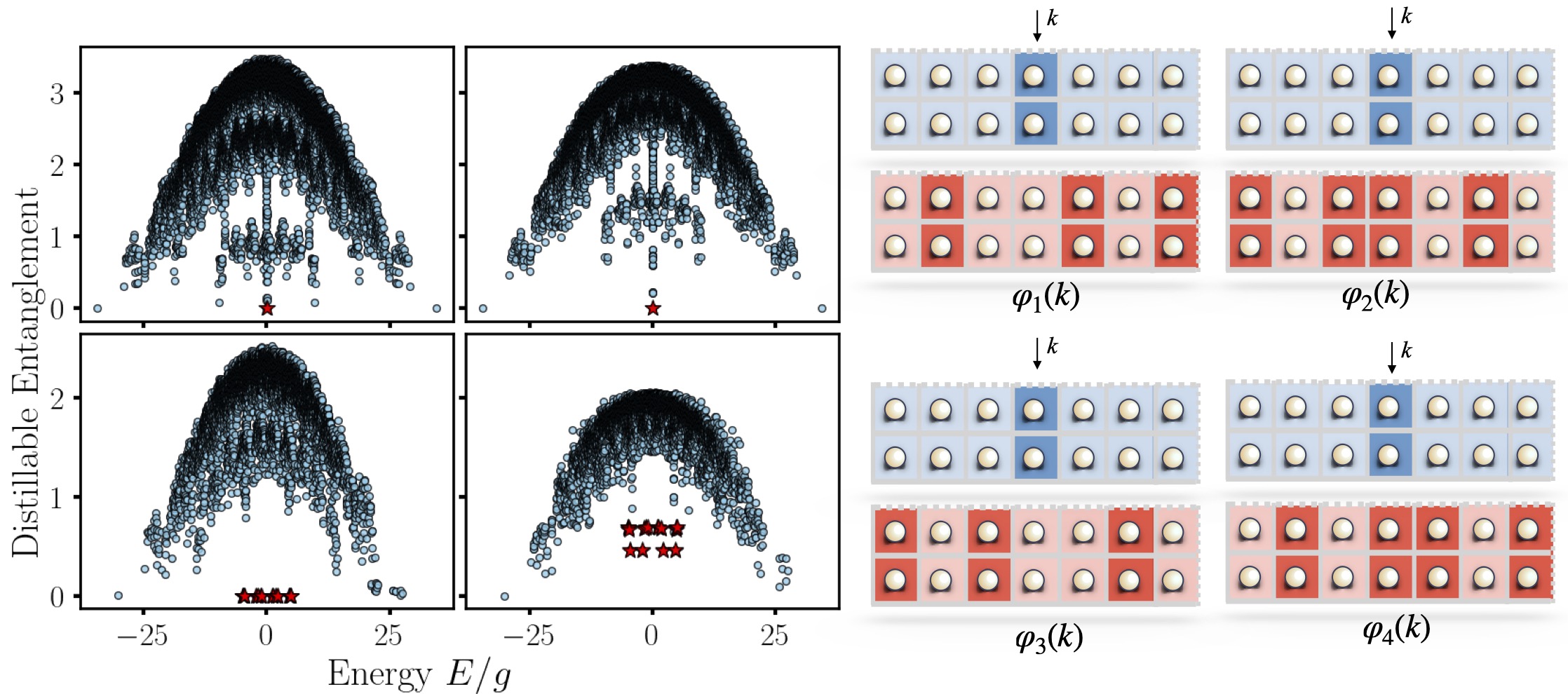
Stabilizer Scars
Quantum many-body scars are eigenstates in non-integrable isolated quantum systems that defy typical thermalization paradigms, violating the eigenstate thermalization hypothesis and quantum ergodicity. We identify exact analytic scar solutions in a 2+1 dimensional lattice gauge theory in a quasi-1d limit as zero-magic stabilizer states. We propose a protocol for their experimental preparation, presenting an opportunity to demonstrate a quantum over classical advantage via simulating the non-equilibrium dynamics of a strongly coupled system. Our results also highlight the importance of magic for gauge theory thermalization, revealing a connection between computational complexity and quantum ergodicity.
This work is supported by the DOE, Office of Science, Office of Nuclear Physics, IQuS, via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science under Award DE-SC0020970, and by the National Science Foundation, NSF DMR-2300172.
Entanglement Properties of SU(2) Gauge Theory
We review recent and present new results on thermalization of nonabelian gauge theory obtained by exact numerical simulation of the real-time dynamics of two-dimensional SU(2) lattice gauge theory. We discuss: (1) tests confirming the Eigenstate Thermalization Hypothesis; (2) the entanglement entropy of sublattices, including the Page curve, the transition from area to volume scaling with increasing energy of the eigenstate and its time evolution that shows thermalization of localized regions to be a two-step process; (3) the absence of quantum many-body scars for j(max)>1/2; (4) the spectral form factor, which exhibits the expected slope-ramp-plateau structure for late times; (5) the entanglement Hamiltonian for SU(2), which has properties in accordance with the Bisognano-Wichmann theorem; and (6) a measure for non-stabilizerness or “magic” that is found to reach its maximum during thermalization. We conclude that the thermalization of nonabelian gauge theories is a promising process to establish quantum advantage.
The authors gratefully acknowledge the scientific support and HPC resources provided by the Erlangen National High Performance Computing Center (NHR@FAU) of the Friedrich-Alexander-Universit ̈at Erlangen-Nu ̈rnberg (FAU) under the NHR project b172da-2. NHR funding is provided by federal and Bavarian state authorities. NHR@FAU hardware is partially funded by the German Research Foundation (DFG 440719683). BM acknowledges support from the U.S. Department of Energy, Office of Science, Nuclear Physics (awards DE-FG02-05ER41367). XY is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science.
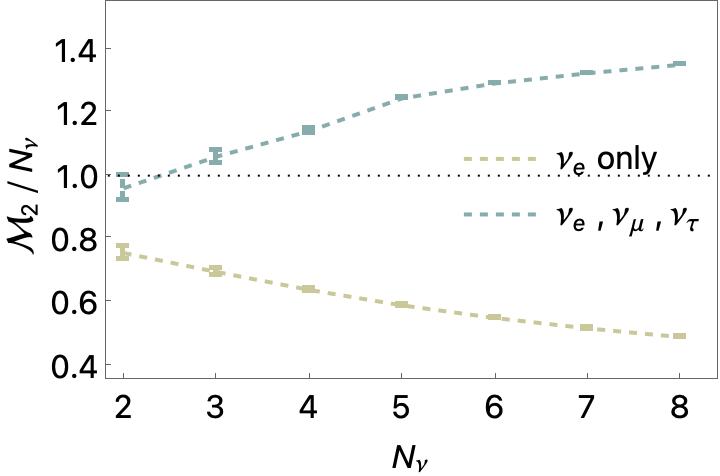
Quantum Magic and Computational Complexity in the Neutrino Sector
We consider the quantum magic in systems of dense neutrinos undergoing coherent flavor transformations, relevant for supernova and neutron-star binary mergers. Mapping the three flavor-neutrino system to qutrits, the evolution of quantum magic is explored in the single scattering angle limit for a selection of initial tensor-product pure states for N< 8 neutrinos. For initial states of electron-type neutrinos, the magic, as measured by the M(2) stabilizer Renyi entropy, is found to decrease with radial distance from the neutrino sphere, reaching a value that lies below the maximum for tensor-product qutrit states. Further, the asymptotic magic per neutrino, M(2)/N, decreases with increasing N. In contrast, the magic evolving from states containing all three flavors reaches values only possible with entanglement, with the asymptotic M(2)/N increasing with N. These results highlight the connection between the complexity in simulating quantum physical systems and the parameters of the Standard Model.
We would like to thank Vincenzo Cirigliano, Henry Froland and Niklas Müller for useful discussions, as well as Emanuele Tirrito for his inspiring presentation at the IQuS workshop Pulses, Qudits and Quantum Simulations, co-organized by Yujin Cho, Ravi Naik, Alessandro Roggero and Kyle Wendt, and for subsequent discussions, an also related discussions with Alessandro Roggero and Kyle Wendt. We would further thank Alioscia Hamma, Thomas Papenbrock and Rahul Trivedi for useful discussions during the IQuS workshop Entanglement in Many-Body Systems: From Nuclei to Quantum Computers and Back, co-organized by Mari Carmen Bañuls, Susan Coppersmith, Calvin Johnson and Caroline Robin. This work was supported by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science, and by the Department of Physics and the College of Arts and Sciences at the University of Washington (Ivan and Martin). This work was also supported, in part, by Universität Bielefeld, and by ERC-885281-KILONOVA Advanced Grant (Caroline). This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 using NERSC awards NP-ERCAP0027114 and NP-ERCAP0029601.
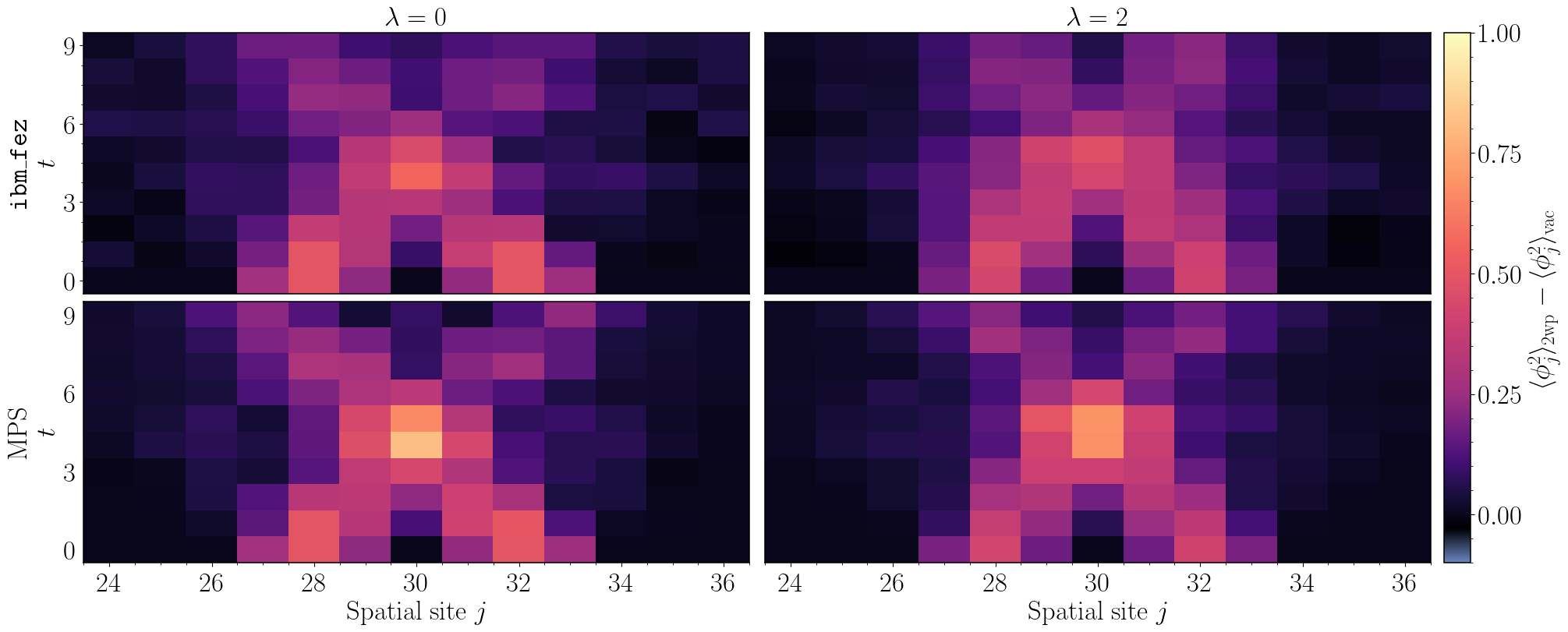
Scalable Quantum Simulations of Scattering in Scalar Field Theory on 120 Qubits
Simulations of collisions of fundamental particles on a quantum computer are expected to have an exponential advantage over classical methods and promise to enhance searches for new physics. Furthermore, scattering in scalar field theory has been shown to be BQP-complete, making it a representative problem for which quantum computation is efficient. As a step toward large-scale quantum simulations of collision processes, scattering of wavepackets in one-dimensional scalar field theory is simulated using 120 qubits of IBM’s Heron superconducting quantum computer ibm_fez. Variational circuits compressing vacuum preparation, wavepacket initialization, and time evolution are determined using classical resources. By leveraging physical properties of states in the theory, such as symmetries and locality, the variational quantum algorithm constructs scalable circuits that can be used to simulate arbitrarily-large system sizes. A new strategy is introduced to mitigate errors in quantum simulations, which enables the extraction of meaningful results from circuits with up to 4924 two-qubit gates and two-qubit gate depths of 103. The effect of interactions is clearly seen, and is found to be in agreement with classical Matrix Product State simulations. The developments that will be necessary to simulate high-energy inelastic collisions on a quantum computer are discussed.
The author thanks Roland Farrell, Marc Illa, Zhiyao Li, Henry Froland, Anthony Ciavarella, and Martin Savage for helpful discussions and insightful comments. This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. This work was also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington. This work has made extensive use of Wolfram Mathematica, python, julia, jupyter notebooks in the conda environment, IBM’s quantum programming environment qiskit, and iTensor in this work. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. This research was done using services provided by the OSG Consortium, which is supported by the National Science Foundation awards #2030508 and #1836650. The author acknowledges the use of IBM Quantum Credits for this work. The views expressed are those of the author, and do not reflect the official policy or position of IBM or the IBM Quantum team.
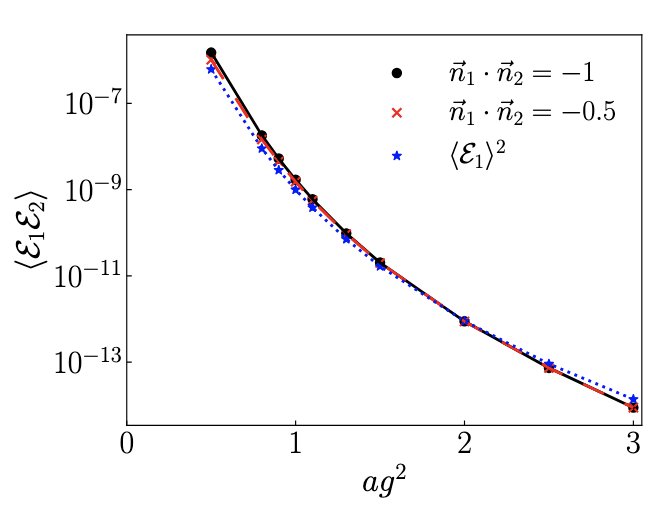
Quantum Computing for Energy Correlators
We study a quantum algorithm to calculate energy correlators for quantum field theories, which consists of ground state preparation, applying source, sink, energy flux and real-time evolution operators and Hadamard test. We discuss how to take the asymptotic detector limit in the Hamiltonian lattice approach. We then calculate the energy correlators for the SU(2) pure gauge theory in 2+1 dimensions on 3 x 3 and 5 x 5 honeycomb lattices with j_max=1/2 at fixed couplings, by using both classical methods and the quantum algorithm studied. The results obtained from the quantum algorithm and the IBM emulator are consistent with the classical methods’ results. We lay out the path forward for calculations in the physical limit.
K.L. was supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics from DE-SC0011090. F.T. and X.Y. were supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0027114.
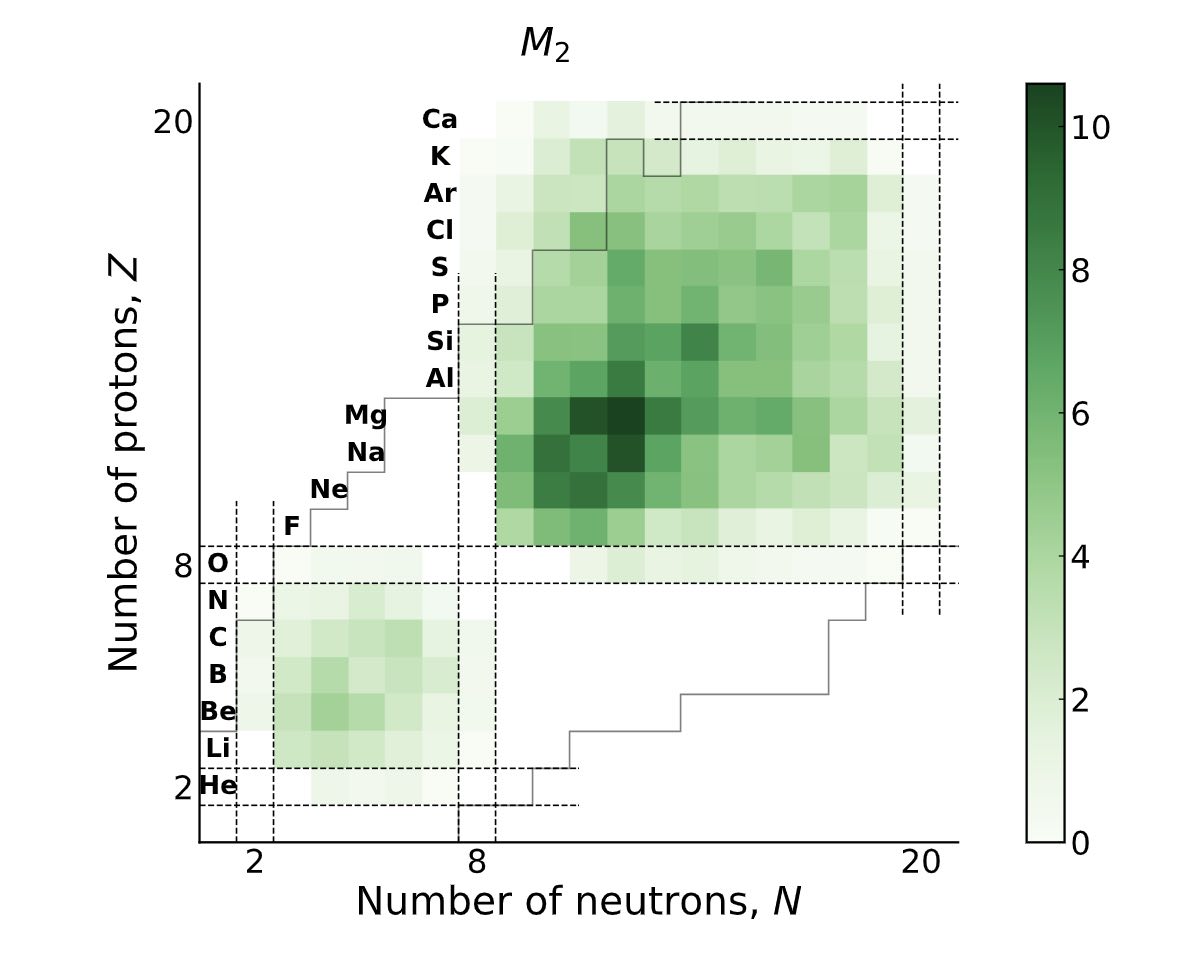
Quantum Magic and Multi-Partite Entanglement in the Structure of Nuclei
Motivated by the Gottesman-Knill theorem, we present a detailed study of the quantum complexity of p-shell and sd-shell nuclei. Valence-space nuclear shell-model wavefunctions generated by the BIGSTICK code are mapped to qubit registers using the Jordan-Wigner mapping (12 qubits for the p-shell and 24 qubits for the sd-shell), from which measures of the many-body entanglement (n-tangles) and magic (non-stabilizerness) are determined. While exact evaluations of these measures are possible for nuclei with a modest number of active nucleons, Monte Carlo simulations are required for the more complex nuclei. The broadly applicable Pauli-String I Z exact (PSIZe-) MCMC technique is introduced to accelerate the evaluation of measures of magic in deformed nuclei (with hierarchical wavefunctions), by factors of ∼ 8 for some nuclei. Significant multi-nucleon entanglement is found in the sd-shell, dominated by proton-neutron configurations, along with significant measures of magic. This is evident not only for the deformed states, but also for nuclei on the path to instability via regions of shape coexistence and level inversion. These results indicate that quantum-computing resources will accelerate precision simulations of such nuclei and beyond. [IQuS@UW-21-088]
This work was supported, in part, by Universität Bielefeld (Caroline, Federico), by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the CRC-TR 211 ’Strong interaction matter under extreme conditions’– project number 315477589 – TRR 211 (Momme), by ERC-885281-KILONOVA Advanced Grant (Caroline), and by the MKW NRW under the funding code NW21-024-A (James). This work also supported by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS)8 under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science, and by the Department of Physics and the College of Arts and Sciences at the University of Washington (Martin). This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02- 05CH11231 using NERSC awards NP-ERCAP0027114 and NP-ERCAP0029601. Some of the computations in this work were performed on the GPU cluster at Bielefeld University. We thank the Bielefeld HPC.NRW team for their support. This research was also partly supported by the cluster computing resource provided by the IT Department at the GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany.
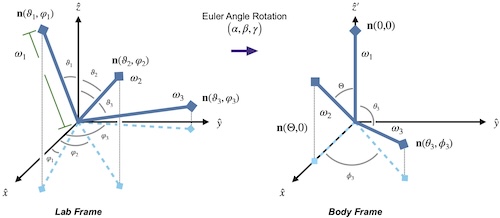
A Fully Gauge-Fixed SU(2) Hamiltonian for Quantum Simulations
We demonstrate how to construct a fully gauge-fixed lattice Hamiltonian for a pure SU(2) gauge theory. Our work extends upon previous work, where a formulation of an SU(2) lattice gauge theory was developed that is efficient to simulate at all values of the gauge coupling. That formulation utilized maximal-tree gauge, where all local gauge symmetries are fixed and a residual global gauge symmetry remains. By using the geometric picture of an SU(2) lattice gauge theory as a system of rotating rods, we demonstrate how to fix the remaining global gauge symmetry. In particular, the quantum numbers associated with total charge can be isolated by rotating between the lab and body frames using the three Euler angles. The Hilbert space in this new “sequestered” basis partitions cleanly into sectors with differing total angular momentum, which makes gauge-fixing to a particular total charge sector trivial, particularly for the charge-zero sector. In addition to this sequestered basis inheriting the property of being efficient at all values of the coupling, we show that, despite the global nature of the final gauge-fixing procedure, this Hamiltonian can be simulated using quantum resources scaling only polynomially with the lattice volume.
DMG is supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. DMG is supported, in part, through the Departmen of Physics and the College of Arts and Sciences at the University of Washington. CFK is supported in part by the Department of Physics, Maryland Center for Fundamental Physics, and the College of Computer, Mathematical, and Natural Sciences at the University of Maryland, College Park. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Department of Energy Computational Science Graduate Fellowship under Award Number DE-SC0020347. CWB was supported by the DOE, Office of Science under contract DE-AC02-05CH11231, partially through Quantum Information Science Enabled Discovery (QuantISED) for High Energy Physics (KA2401032)
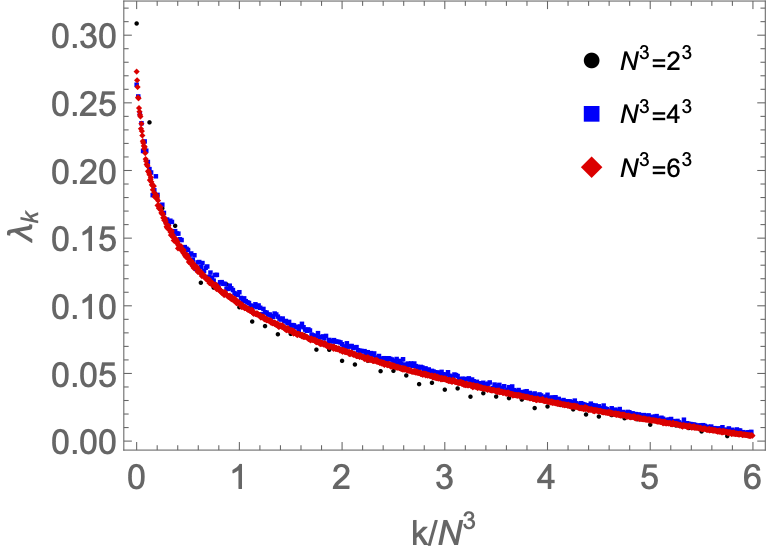
The Nonabelian Plasma is Chaotic
Nonabelian gauge theories are chaotic in the classical limit. We discuss new evidence from SU(2) lattice gauge theory that they are also chaotic at the quantum level. We also describe possible future studies aimed at discovering the consequences of this insight. Based on a lecture presented by the first author at the Particles and Plasmas Symposium 2024.
The authors gratefully acknowledge the scientific support and HPC resources provided by the Erlangen National High Performance Computing Center (NHR@FAU) of the Friedrich-Alexander-Universit ̈at Erlangen-Nurnberg (FAU) under the NHR project b172da-2. NHR funding is provided by federal and Bavarian state authorities. NHR@FAU hardware is partially funded by the German Research Foundation (DFG 440719683). BM and XY acknowledge support from the U.S. Department of Energy, Office of Science, Nuclear Physics (awards DE-FG02-05ER41367 and DE-SC0020970).
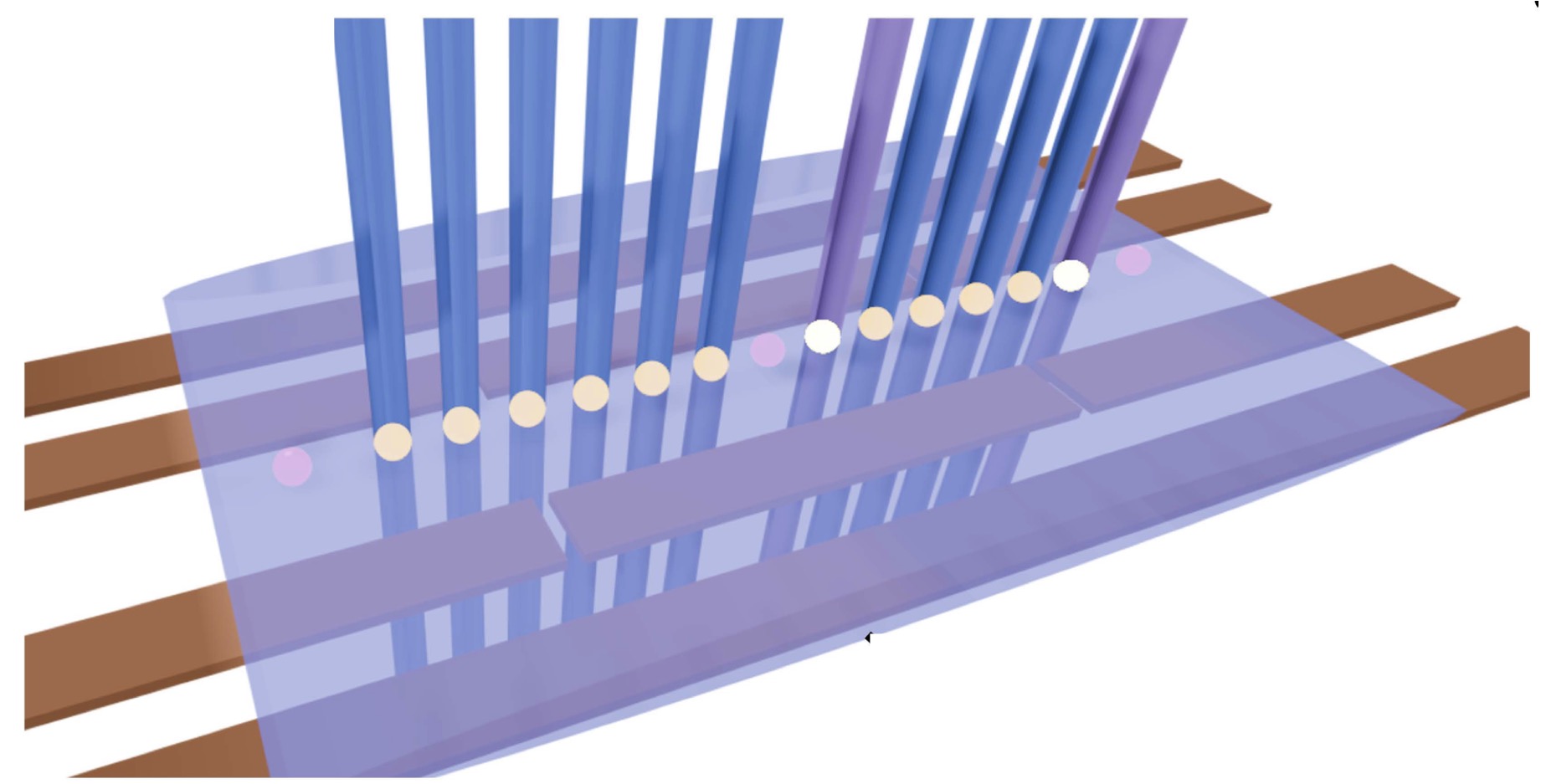
Quantum Computing Universal Thermalization Dynamics in a (2+1)D Lattice Gauge Theory
Simulating nonequilibrium phenomena in strongly-interacting quantum many-body systems, including thermalization, is a promising application of near-term and future quantum computation. By performing experiments on a digital quantum computer consisting of fully-connected optically-controlled trapped ions, we study the role of entanglement in the thermalization dynamics of a Z2 lattice gauge theory in 2+1 spacetime dimensions. Using randomized-measurement protocols, we efficiently learn a classical approximation of nonequilibrium states that yields the gap-ratio distribution and the spectral form factor of the entanglement Hamiltonian. These observables exhibit universal early-time signals for quantum chaos, a prerequisite for thermalization. Our work, therefore, establishes quantum computers as robust tools for studying universal features of thermalization in complex many-body systems, including in gauge theories.
This work is supported by the DOE, Office of Science, Office of Nuclear Physics, IQuS (\url{https://iqus.uw.edu}), via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science under Award DE-SC0020970 and by the National Science Foundation’s Quantum Leap Challenge Institute for Robust Quantum Simulation under Award OMA-2120757 and by the Department of Energy’s (DOE’s) QDOE Office of Science Early Career Award DE-SC0020271
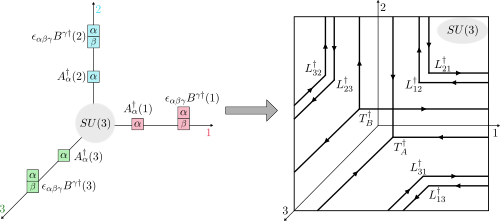
Loop-string-hadron approach to SU(3) lattice Yang-Mills theory: Gauge invariant Hilbert space of a trivalent vertex
The construction of gauge invariant states of SU(3) lattice gauge theories has garnered new interest in recent years, but implementing them is complicated by the difficulties of SU(3) Clebsch-Gordon coefficients. In the loop-string-hadron (LSH) approach to lattice gauge theories, the elementary excitations are strictly gauge invariant, and constructing the basis requires no knowledge of Clebsch-Gordon coefficients. Originally developed for SU(2), the LSH formulation was recently generalized to SU(3), but limited to one spatial dimension. In this work, we generalize the LSH approach to constructing the basis of SU(3) gauge invariant states at a trivalent vertex — the essential building block to multidimensional space. A direct generalization from the SU(2) vertex yields a legitimate basis; however, in certain sectors of the Hilbert space, the naive LSH basis vectors so defined suffer from being nonorthogonal. The issues with orthogonality are directly related to the “missing label” or “outer multiplicity” problem associated with SU(3) tensor products, and may also be phrased in terms of Littlewood-Richardson coefficients or the need for a “seventh Casimir” operator. The states that are unaffected by the problem are orthonormalized in closed form. For the sectors that are afflicted, we discuss the nonorthogonal bases and their orthogonalization. A few candidates for seventh Casimir operators are readily constructed from the suite of LSH gauge-singlet operators. The diagonalization of a seventh Casimir represents one prescriptive solution towards obtaining a complete orthonormal basis, but a closed-form general solution remains to be found.
Work by JRS was supported by the U.S. Department of Energy (DOE), Office of Science under contract DE-AC02-05CH11231, partially through Quantum Information Science Enabled Discovery (QuantISED) for High Energy Physics (KA2401032). JRS and SK both received sup- port from the U.S. Department of Energy’s Office of Science Early Career Award under award DE-SC0020271, for theoretical developments for simulating lattice gauge theories on quantum computers. SK acknowledges support by the U.S. DOE, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (award no. DE-SC0020970), and by the DOE QuantISED program through the theory consortium “Intersections of QIS and Theoretical Particle Physics” at Fermilab (Fermilab subcontract no. 666484). SK further acknowledges the support from the Department of Physics and the College of Arts and Sciences at the University of Washington. Research of IR is supported by the OPERA award (FR/SCM/11 Dec-2020/PHY) from BITS-Pilani, the Start-up Research Grant (SRG/2022/000972) and Core-Research Grant (CRG/2022/007312) from ANRF, India and the cross-discipline research fund (C1/23/185) from BITS-Pilani. AN is supported by the Start-up Research Grant (SRG/2022/000972) from ANRF, India received by IR.
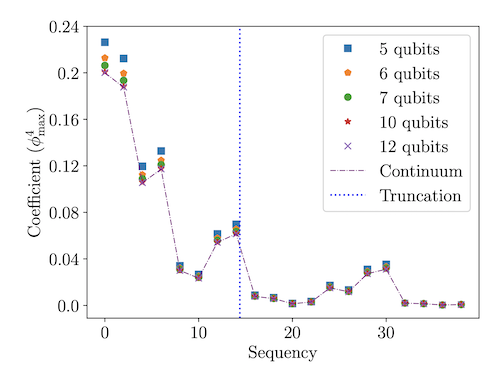
Sequency Hierarchy Truncation (SeqHT) for Adiabatic State Preparation and Time Evolution in Quantum Simulations
We introduce the Sequency Hierarchy Truncation (SeqHT) scheme for reducing the resources required for state preparation and time evolution in quantum simulations, based upon a truncation in sequency. For the λφ4 interaction in scalar field theory, or any interaction with a polynomial expansion, upper bounds on the contributions of operators of a given sequency are derived. For the systems we have examined, observables computed in sequency-truncated wavefunctions, including quantum correlations as measured by magic, are found to step-wise converge to their exact values with increasing cutoff sequency. The utility of SeqHT is demonstrated in the adiabatic state preparation of the λφ4 anharmonic oscillator ground state using IBM’s quantum computer ibm_sherbrooke. Using SeqHT, the depth of the required quantum circuits is reduced by ∼ 30%, leading to significantly improved determinations of observables in the quantum simulations. More generally, SeqHT is expected to lead to a reduction in required resources for quantum simulations of systems with a hierarchy of length scales.
This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. This work was supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington. We acknowledge the use of IBM Quantum services for this work.
Universal corrections to the superfluid gap in a cold Fermi gas
A framework for computing the superfluid gap in an effective field theory (EFT) of fermions interacting via momentum independent contact forces is developed. The leading universal corrections in the EFT are one-loop in-medium effects at the Fermi surface, and reproduce the well-known Gor’kov-Melik-Barkhudarov result. The complete subleading universal corrections are presented here, and include one-loop effects away from the Fermi surface, two-loop in-medium effects, as well as modifications to the fermion propagator. Together, these effects are found to reduce the gap at low densities. Applications to neutron superfluidity in neutron stars are discussed.
This work was supported by the Swiss National Science Foundation (SNSF) under grant numbers 200021_192137 and PCEFP2_203335, by the U. S. Department of Energy grant DE-FG02-97ER-41014 (UW Nuclear Theory) and by the U. S. Department of Energy grant DE-SC0020970, (InQubator for Quantum Simulation).
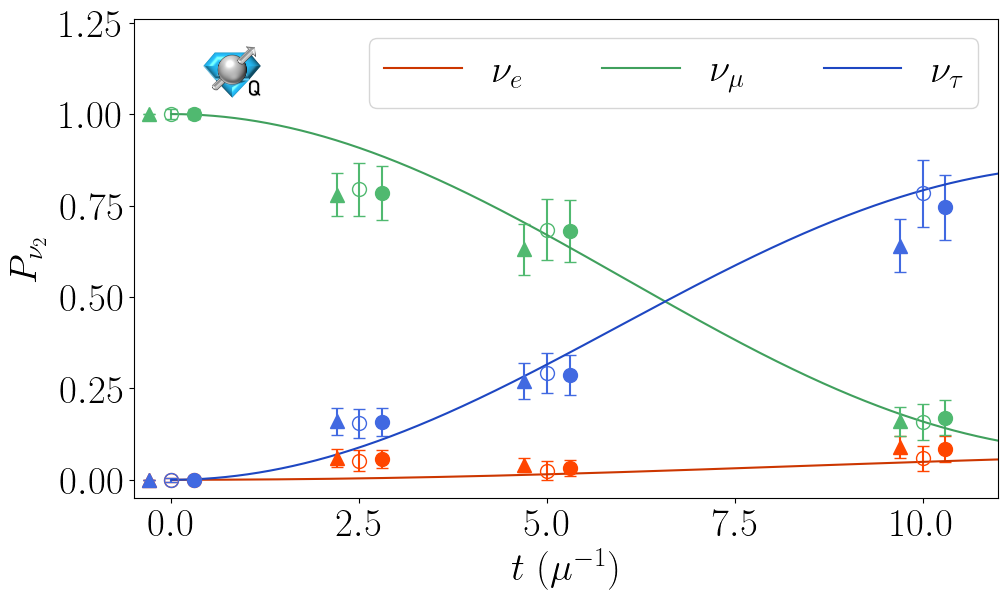
Qutrit and Qubit Circuits for Three-Flavor Collective Neutrino Oscillations
We explore the utility of qutrits and qubits for simulating the flavor dynamics of dense neutrino systems. The evolution of such systems impacts some important astrophysical processes, such as core-collapse supernovae and the nucleosynthesis of heavy nuclei. Many-body simulations require classical resources beyond current computing capabilities for physically relevant system sizes. Quantum computers are therefore a promising candidate to efficiently simulate the many-body dynamics of collective neutrino oscillations. Previous quantum simulation efforts have primarily focused on properties of the two-flavor approximation due to their direct mapping to qubits. Here, we present new quantum circuits for simulating three-flavor neutrino systems on qutrit- and qubit-based platforms, and demonstrate their feasibility by simulating systems of two, four and eight neutrinos on IBM and Quantinuum quantum computers.
This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS)9 under DOE (NP) Award No. DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Turro, Bhaskar, Chernyshev), and the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (DOE) (Illa). This work is also supported, in part, through the Department of Physics12 and the College of Arts and Sciences at the University of Washington. This research used resources of the Oak Ridge Leadership Computing Facility (OLCF), which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725. We acknowledge the use of IBM Quantum services for this work.
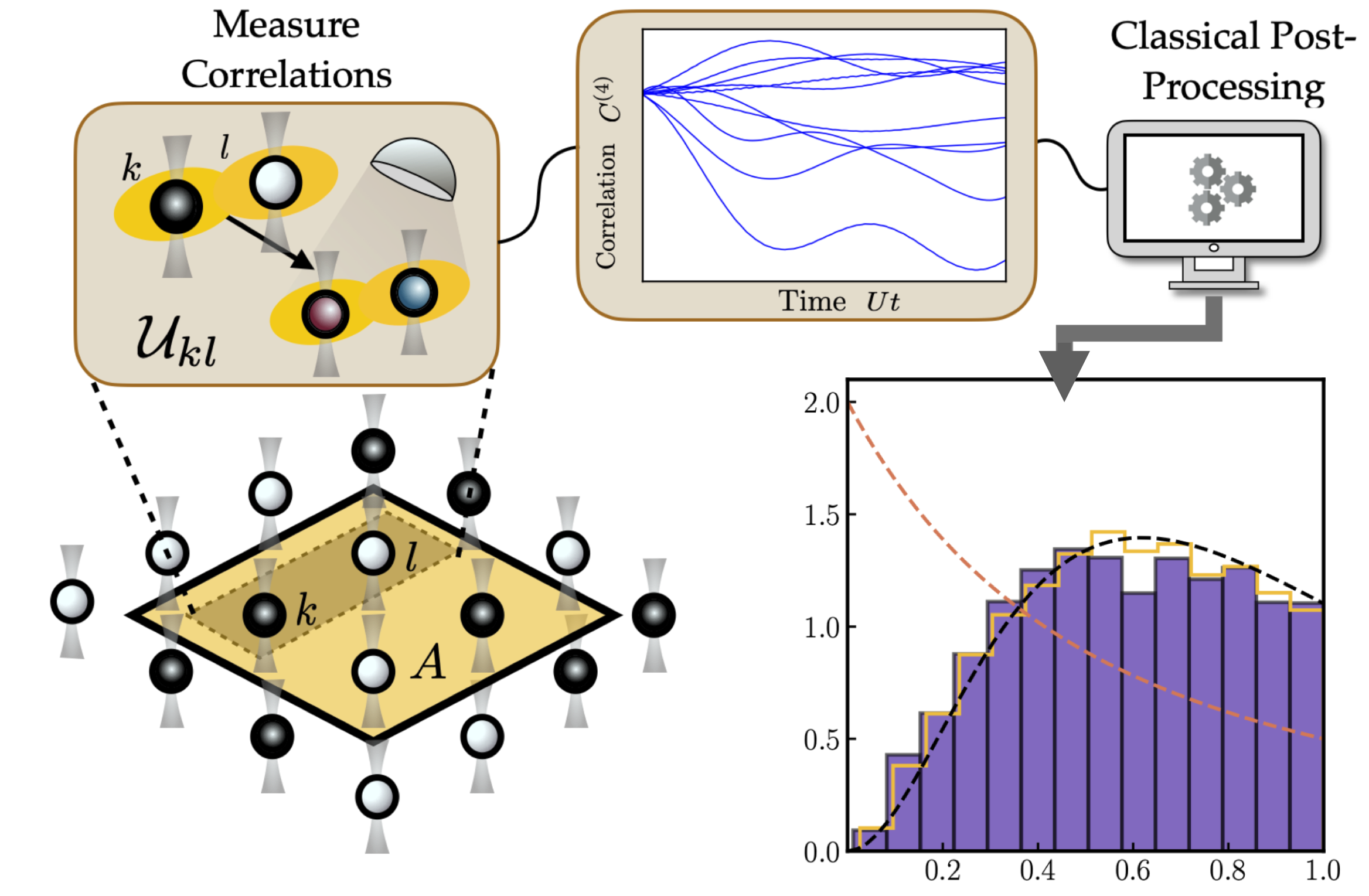
Entanglement Structure of Non-Gaussian States and How to Measure It
Rapidly growing capabilities of quantum simulators to probe quantum many-body phenomena require new methods to characterize increasingly complex states. We present a protocol that constrains quantum states by experimentally measured correlation functions which only scales polynomially with system size. This method enables measurement of a quantum state’s entanglement structure, opening a new route to study entanglement-related phenomena. Our approach extends Gaussian state parameterizations by systematically incorporating higher-order correlations. We show the protocol’s usefulness in conjunction with current and forthcoming experimental capabilities, focusing on weakly interacting fermions as a proof of concept. Here, the lowest non-trivial expansion quantitatively predicts early time thermalization dynamics, including signaling the on-set of quantum chaos indicated by the entanglement Hamiltonian.
This work is supported by the DOE, Office of Science, Office of Nuclear Physics, IQuS (\url{https://iqus.uw.edu}), via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science under Award DE-SC0020970 and by the European Union’s Horizon Europe research and innovation program under Grant Agreement No. 101113690 (PASQuanS2.1), the ERC Starting grant QARA (Grant No.~101041435), the EU-QUANTERA project TNiSQ (N-6001), and by the Austrian Science Fund (FWF): COE 1 and quantA. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington
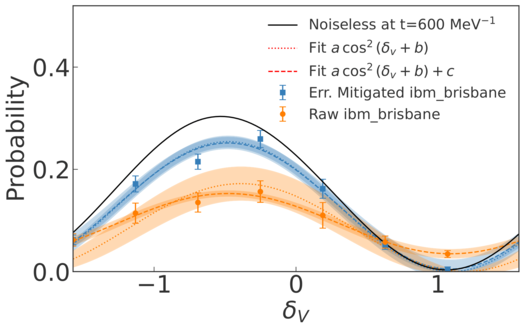
Evaluation of phase shifts for non-relativistic elastic scattering using quantum computers
Simulations of scattering processes are essential in understanding the physics of our universe. Computing relevant scattering quantities from ab initio methods is extremely difficult on classical devices because of the substantial computational resources needed. This work reports the development of an algorithm that makes it possible to obtain phase shifts for generic non-relativistic elastic scattering processes on a quantum computer. Such algorithm is based on extracting phase shifts from the direct implementation of the real-time evolution. The algorithm is improved by a variational procedure, making it more accurate and resistant to the noise of quantum . The reliability of the algorithm is first demonstrated by means of classical numerical simulations for different potentials, and later tested on existing quantum hardware, specifically on IBM quantum processors.
This work was supported in part by the U.S. De- partment of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quan- tum Horizons: QIS Research and Innovation for Nuclear Science. This work was prepared in part by LLNL under Contract No. DE- AC52-07NA27344 with sup- port from the U.S. Department of Energy, Office of Sci- ence, Office of Nuclear Physics (under Work Proposal No. SCW1730). This work was enabled by the use of advanced compu- tational, storage, and networking infrastructure provided by the Hyak supercomputer system at the University of Washington (https://hyak.uw.edu/).
Quarkonium Polarization in Medium from Open Quantum Systems and Chromomagnetic Correlators
We study the spin-dependent in-medium dynamics of quarkonia by using the potential nonrelativistic QCD (pNRQCD) and the open quantum system framework. We consider the pNRQCD Lagrangian valid up to the order. r/M^0=r and r^0/M=1/M in the double power counting. By considering the Markovian condition and applying the Wigner transformation upon the diagonal spin components of the quarkonium density matrix with the semiclassical expansion, we systematically derive the Boltzmann transport equation for quarkonia with polarization dependence in the quantum optical limit. Unlike the spin-independent collision terms governed by certain chromoelectric field correlators, new gauge invariant correlators of chromomagnetic fields determine the recombination and dissociation terms with polarization dependence at the order we are working. We also derive a Lindblad equation describing the in-medium transitions between spin-singlet and spin-triplet heavy quark-antiquark pairs in the quantum Brownian motion limit. The Lindblad equation is governed by new transport coefficients defined in terms of the chromomagnetic field correlators. Our formalism is generic and valid for both weakly-coupled and strongly-coupled quark gluon plasmas. It can be further applied to study spin alignment of vector quarkonia in heavy ion collisions.
This work was supported in part by National Science and Technology Council (Taiwan) under Grant No. MOST 110-2112-M-001-070-MY, by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science.
Three-flavor Collective Neutrino Oscillations on D-Wave’s Advantage Quantum Annealer
In extreme environments such as core-collapse supernovae, neutron-star mergers, and the early Universe, neutrinos are dense enough that their self-interactions significantly affect, if not dominate, their flavor dynamics. In order to develop techniques for characterizing the resulting quantum entanglement, I present the results of simulations of Dirac neutrino-neutrino interactions that include all three physical neutrino flavors and were performed on D-Wave Inc.’s Advantage 5000+ qubit annealer. These results are checked against those from exact classical simulations, which are also used to compare the Dirac neutrino-neutrino interactions to neutrino-antineutrino and Majorana neutrino-neutrino interactions. The D-Wave Advantage annealer is shown to be able to reproduce time evolution with the precision of a classical machine for small numbers of neutrinos and to do so without Trotter errors. However, it suffers from poor scaling in qubit-count with the number of neutrinos. Two approaches to improving the qubit-scaling are discussed, but only one of the two shows promise.
This work was supported in part by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) [154] under Award Number DOE (NP) Award DE- SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science and by the Quantum Computing Summer School 2023 at Los Alamos National Laboratory (LANL).
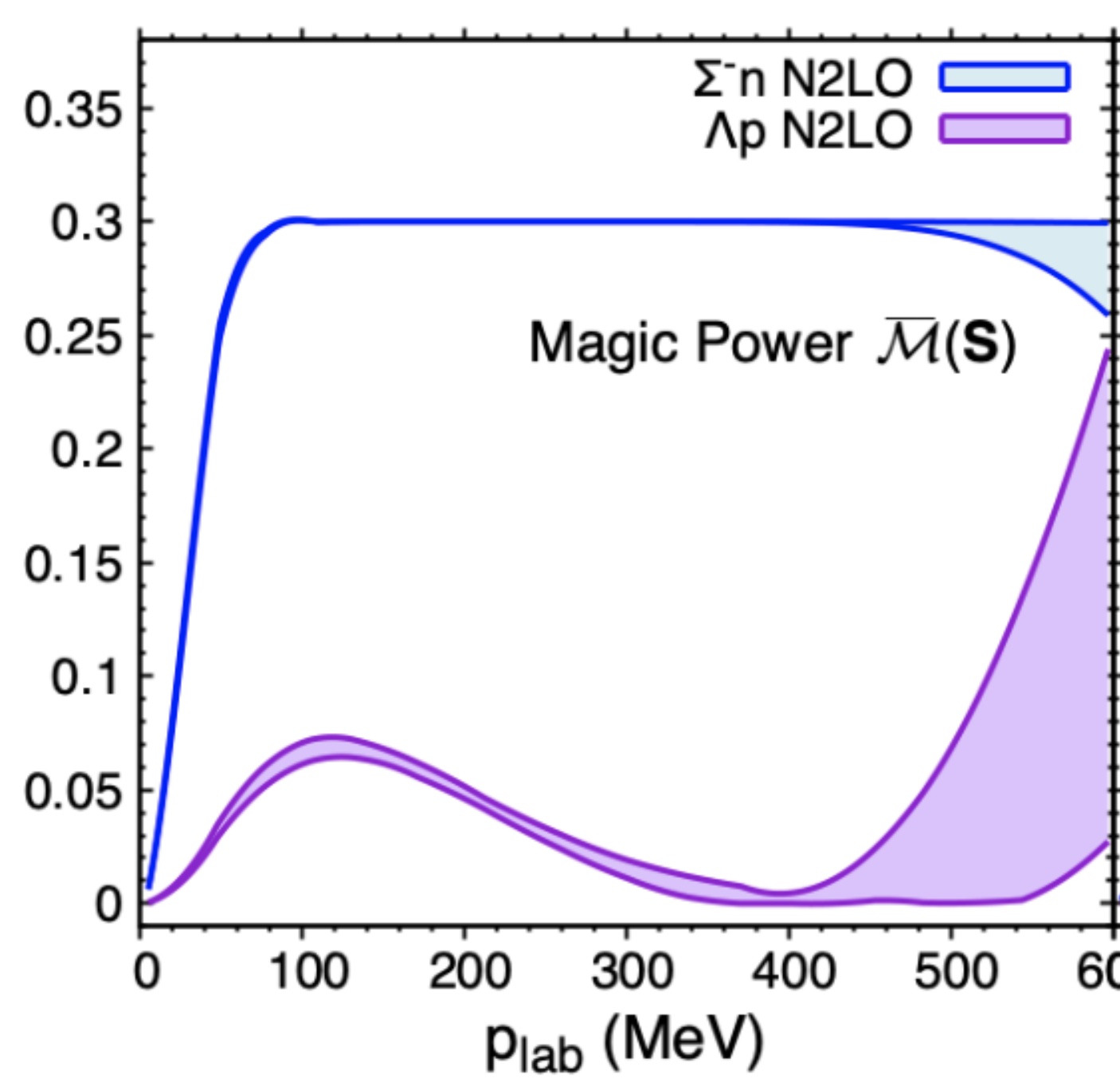
The Magic in Nuclear and Hypernuclear Forces
Toward an improved understanding of the role of quantum information in nuclei and exotic matter, we examine the magic (non-stabilizerness) in low-energy strong interaction processes. As stabilizer states can be prepared efficiently using classical computers, and include classes of entangled states, it is magic and fluctuations in magic, along with entanglement, that determine resource requirements for quantum simulations. As a measure of fluctuations in magic induced by scattering, the “magic power” of the S-matrix is introduced. Using experimentally determined scattering phase shifts and mixing parameters, the magic power in nucleon-nucleon and hyperon-nucleon scattering, along with the magic in the deuteron, are found to exhibit interesting features. The Sigma-minus baryon is identified as a potential candidate catalyst for enhanced spreading of magic and entanglement in dense matter, depending on in-medium decoherence.
This work was supported, in part, by Universität Bielefeld and ERC- 885281-KILONOVA Advanced Grant (Caroline), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science4 (Martin). This work was supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.
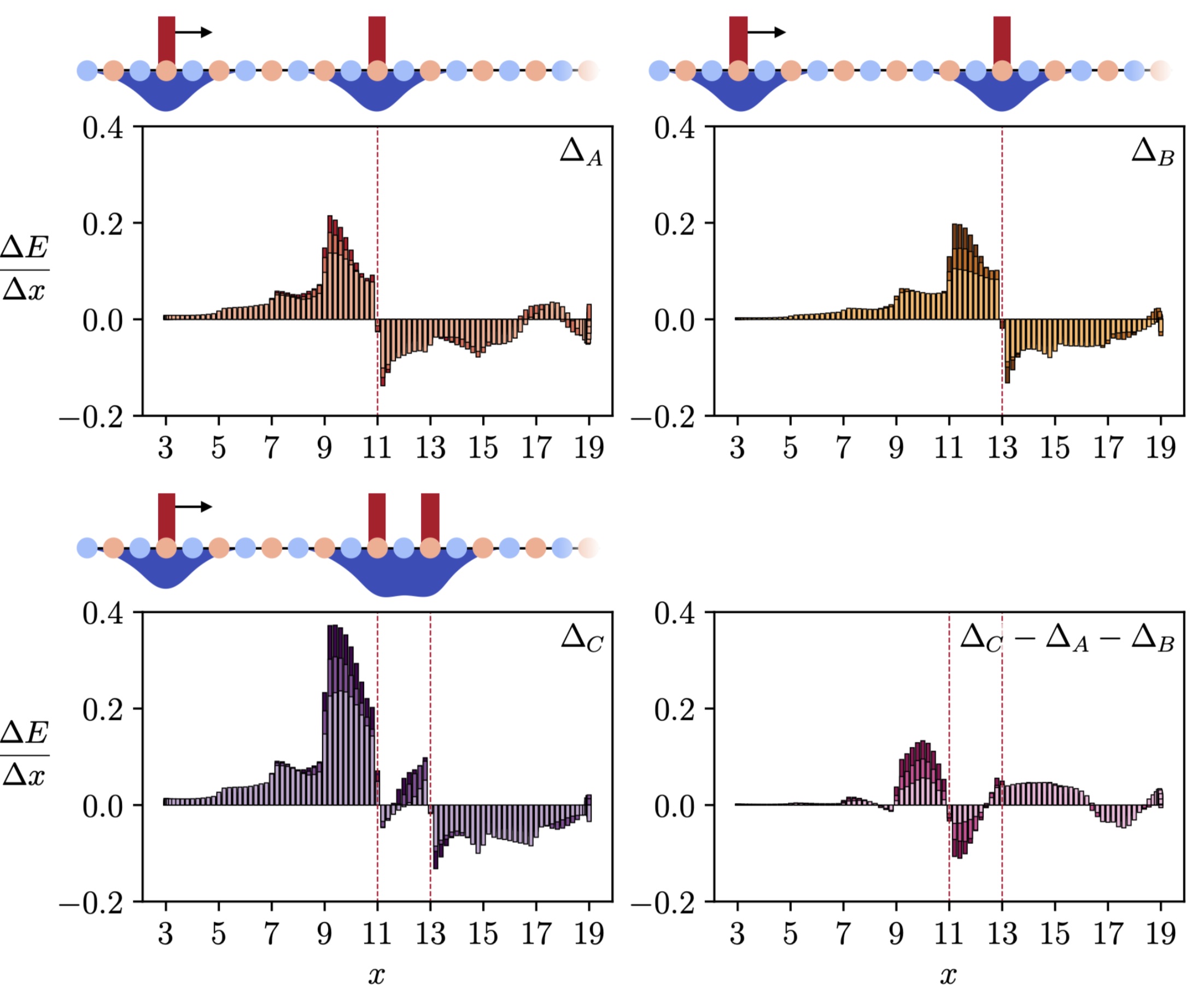
Steps Toward Quantum Simulations of Hadronization and Energy-Loss in Dense Matter
A framework for simulating the real-time dynamics of particles in dense matter using quantum computers is developed. This formalism is used to simulate heavy-hadrons propagating through a dense medium in the Schwinger model. Measurements of the time-dependent energy and charge density are used to identify mechanisms responsible for energy loss and hadron production (hadronization). A study of entanglement dynamics highlights the importance of quantum coherence between the particles that make up the dense medium. Throughout this work, care is taken to isolate, and remove, phenomena that arise solely from a finite lattice spacing. An efficient method and the corresponding quantum circuits for preparing ground states in the presence of heavy mesons are presented. These circuits are used to estimate the resources required to simulate in-medium energy loss and hadronization in the Schwinger model using quantum computers.
This work was supported, in part, by the U.S. Department of Energy grant DE-FG02-97ER-41014 (Roland), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Roland, Martin), the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (DOE) (Marc). This work is also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.
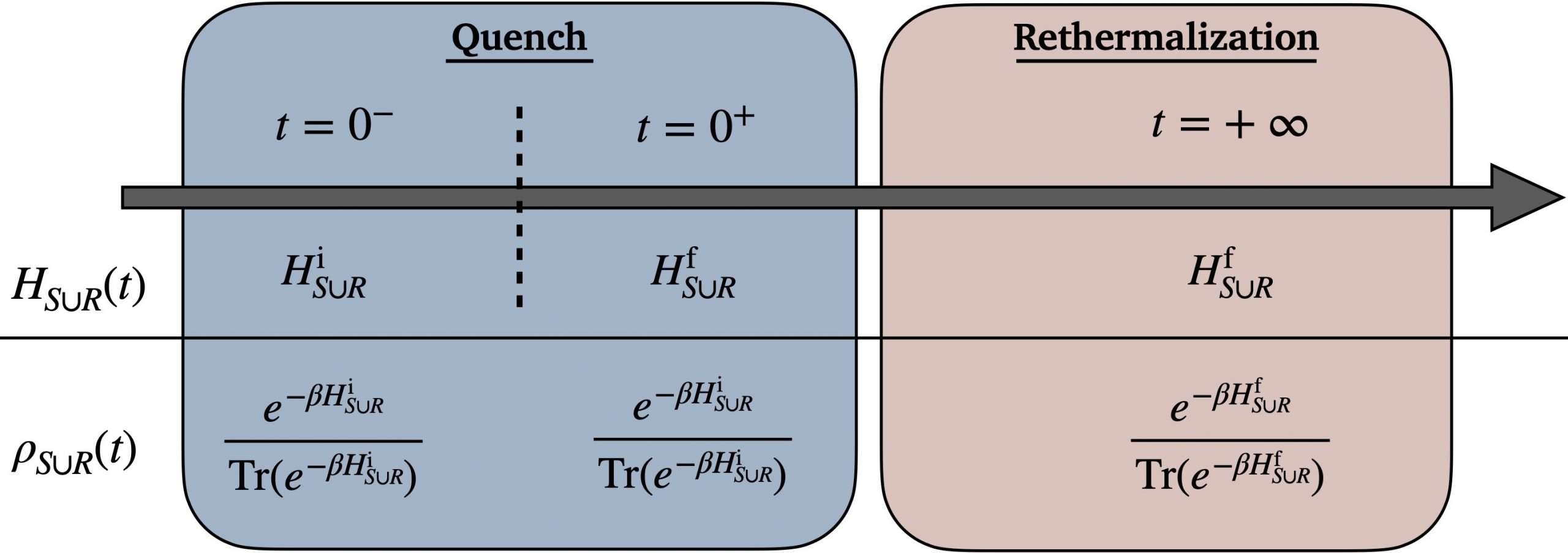
Quantum thermodynamics of nonequilibrium processes in lattice gauge theories
A key objective in nuclear and high-energy physics is to describe nonequilibrium dynamics of matter, e.g., in the early universe and in particle colliders, starting from the Standard Model. Classical-computing methods, via the framework of lattice gauge theory, have experienced limited success in this mission. Quantum simulation of lattice gauge theories holds promise for overcoming computational limitations. Because of local constraints (Gauss’s laws), lattice gauge theories have an intricate Hilbert-space structure. This structure complicates the definition of thermodynamic properties of systems coupled to reservoirs during equilibrium and nonequilibrium processes. We show how to define thermodynamic quantities such as work and heat using strong-coupling thermodynamics, a framework that has recently burgeoned within the field of quantum thermodynamics. Our definitions suit instantaneous quenches, simple nonequilibrium processes undertaken in quantum simulators. To illustrate our framework, we compute the work and heat exchanged during a quench in a $Z_2$ lattice gauge theory coupled to matter in 1+1 dimensions. The thermodynamic quantities, as functions of the quench parameter, evidence an expected phase transition. Generally, we derive a simple relation between a quantum many-body system’s entanglement Hamiltonian, measurable with quantum-information-processing tools, and the Hamiltonian of mean force, used to define strong-coupling thermodynamic quantities.
This work was supported in part by the National Science Foundation (NSF) Quantum Leap Challenge Institutes (QLCI) (award no. OMA-2120757), by the Department of Energy (DOE), Office of Science, Early Career Award (award no. DESC0020271), and by the Department of Physics, Maryland Center for Fundamental Physics, and the College of Computer, Mathematical, and Natural Sciences at the University of Maryland, College Park, and the Simons Foundation through the Simons Foundation Emmy Noether Fellows Program at Perimeter Institute, by the John Templeton Foundation (award no. 62422), and by the DOE, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (award no. DE-SC0020970).
Qu8its for Quantum Simulations of Lattice Quantum Chromodynamics
We explore the utility of d=8 qudits, qu8its, for quantum simulations of the dynamics of 1+1D SU(3) lattice quantum chromodynamics, including a mapping for arbitrary numbers of flavors and lattice size and a re-organization of the Hamiltonian for efficient time-evolution. Recent advances in parallel gate applications, along with the shorter application times of single-qudit operations compared with two-qudit operations, lead to significant projected advantages in quantum simulation fidelities and circuit depths using qu8its rather than qubits. The number of two-qudit entangling gates required for time evolution using qu8its is found to be more than a factor of five fewer than for qubits. We anticipate that the developments presented in this work will enable improved quantum simulations to be performed using emerging quantum hardware.
This work was supported, in part, by Universität Bielefeld and ERC-885281-KILONOVA Advanced Grant (Caroline Robin), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, Inqubator for Quantum Simulation (IQuS)9 under Award Number DOE (NP) Award DE-SC0020970 (Martin Savage), and the Quantum Science Center (QSC), a National Quantum Information Science Research Center of the U.S. Department of Energy (Marc Illa). This work was supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.
Real-time Dynamics of the Schwinger Model as an Open Quantum System with Neural Density Operators
Ab-initio simulations of multiple heavy quarks propagating in a Quark-Gluon Plasma are computationally difficult to perform due to the large dimension of the space of density matrices. This work develops machine learning algorithms to overcome this difficulty by approximating exact quantum states with neural network parametrisations, specifically Neural Density Operators. As a proof of principle demonstration in a QCD-like theory, the approach is applied to solve the Lindblad master equation in the 1+1D lattice Schwinger Model as an open quantum system. Neural Density Operators enable the study of in-medium dynamics on large lattice volumes, where multiple-string interactions and their effects on string-breaking and recombination phenomena can be studied. Thermal properties of the system at equilibrium can also be probed with these methods by variationally constructing the steady state of the Lindblad master equation. Scaling of this approach with system size is studied, and numerical demonstrations on up to 32 spatial lattice sites and with up to 3 interacting strings are performed.
This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under grant Contract Numbers DE-SC0011090, by Early Career Award DE-SC0021006 and by the Simons Foundation grant 994314 (Simons Collaboration on Confinement and QCD Strings), by he U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Co-design Center for Quantum Advantage (C2QA) under contract number DE-SC0012704, by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science, by the U.S. National Science Foundation under Cooperative Agreement PHY-2019786 (The NSF AI Institute for Artificial Intelligence and Fundamental Interactions, http://iaifi.org/). The authors acknowledge the MIT SuperCloud and Lincoln Laboratory Supercomputing Center [68] for providing HPC resources that have contributed to the research results reported within this paper.
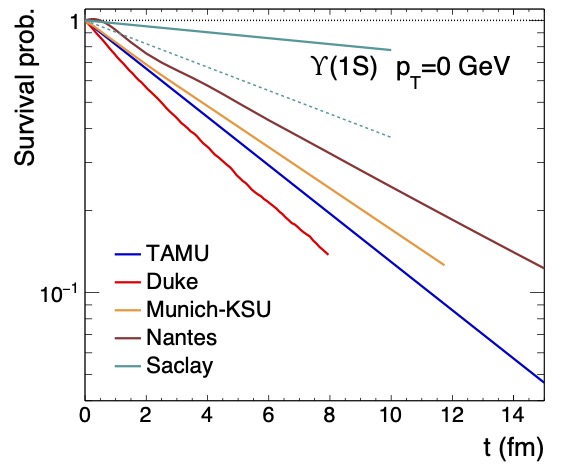
Comparative Study of Quarkonium Transport in Hot QCD Matter
This document summarizes the efforts of the EMMI Rapid Reaction Task Force on “Suppression and (re)generation of quarkonium in heavy-ion collisions at the LHC”, centered around their 2019 and 2022 meetings. It provides a review of existing experimental results and theoretical approaches, including lattice QCD calculations and semiclassical and quantum approaches for the dynamical evolution of quarkonia in the quark-gluon plasma as probed in high-energy heavy-ion collisions. The key ingredients of the transport models are itemized to facilitate comparisons of calculated quantities such as reaction rates, binding energies, and nuclear modification factors. A diagnostic assessment of the various results is attempted and coupled with an outlook for the future.
This work was supported in part by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the CRC-TR 211 ’Strong-interaction matter under extreme conditions’– project number 315477589 – TRR 211; by the Xunta de Galicia (Centro singular de investigacion de Galicia accreditation 2019-2022), the European Union ERDF, the “Maria de Maeztu” Units of Excellence program under projects CEX2020-001035-M and CEX2019-000918-M, the Spanish Research State Agency under projects PID2020-119632GB-I00 and PID2019-105614GB- C21, and the European Research Council under project ERC-2018-ADG-835105 YoctoLHC; by the Generalitat de Catalunya under grant 2021-SGR-249, by U.S. Department of Energy award No. DE-SC0013470; by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics through Contract No. DE-SC0012704; by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science; by the Centre national de la recherche scientifique (CNRS) and R ́egion Pays de la Loire and acknowledges the support of Narodowe Centrum Nauki under grant no. 2019/34/E/ST2/00186, by the European Union’s Horizon 2020 research and innovation program under grant agreement No 824093 (STRONG-2020), by the U.S. Department of Energy Award No. DE-SC0019095 and is grateful for the support and hospitality of the Fermilab theory group; by the U.S. National Science Foundation under grant nos. PHY-1913286 and PHY-2209335; by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics through the Topical Collaboration in Nuclear Theory on Heavy-Flavor Theory (HEFTY) for QCD Matter under award no. DE-SC0023547.
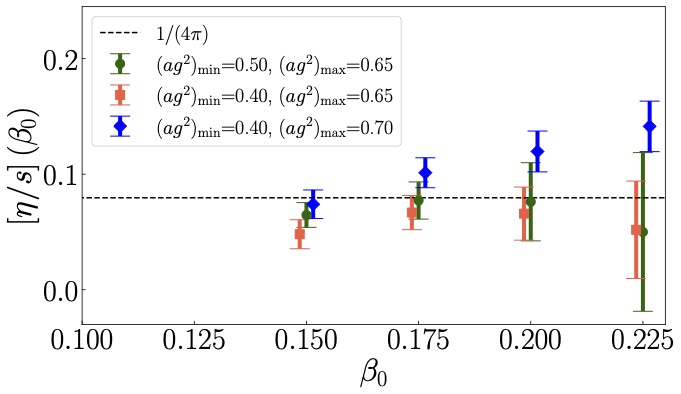
Classical and Quantum Computing of Shear Viscosity for 2+1D SU(2) Gauge Theory
We perform a nonperturbative calculation of the shear viscosity for 2+1-dimensional SU(2) gauge theory by using the lattice Hamiltonian formulation. The retarded Green’s function of the stress-energy tensor is calculated from real time evolution via exact diagonalization of the lattice Hamiltonian with a local Hilbert space truncation and the shear viscosity is obtained via the Kubo formula. When taking the continuum limit, we account for the renormalization group flow of the coupling but no additional operator renormalization. We find the ratio of the shear viscosity and the entropy density eta/s is consistent with a well-known holographic result 1/(4 pi) at several temperatures on a 4×4 hexagonal lattice with the local electric representation truncated at j_max=1/2. We also find the ratio of the spectral function and frequency rho^(xy)(omega)/omega exhibits a peak structure when the frequency is small. Both exact diagonalization method and simple matrix product state classical simulation method beyond j_max=1/2 on bigger lattices require exponentially growing resources. So we develop a quantum computing method to calculate the retarded Green’s function and analyze various systematics of the calculation including j_max truncation and finite size effects and Trotter errors. We test our quantum circuit on both the Quantinuum emulator and the IBM simulator for a small lattice and obtain results consistent with the classical computing ones.
This work is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. A.C. acknowledges support from the U.S. Department of Energy, Office of Science under contract DE-AC02-05CH11231, partially through Quantum Information Science Enabled Discovery (QuantISED) for High Energy Physics (KA2401032). This research used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE- AC05-00OR22725. We acknowledge the use of Quantinum and IBM Quantum services for this work.
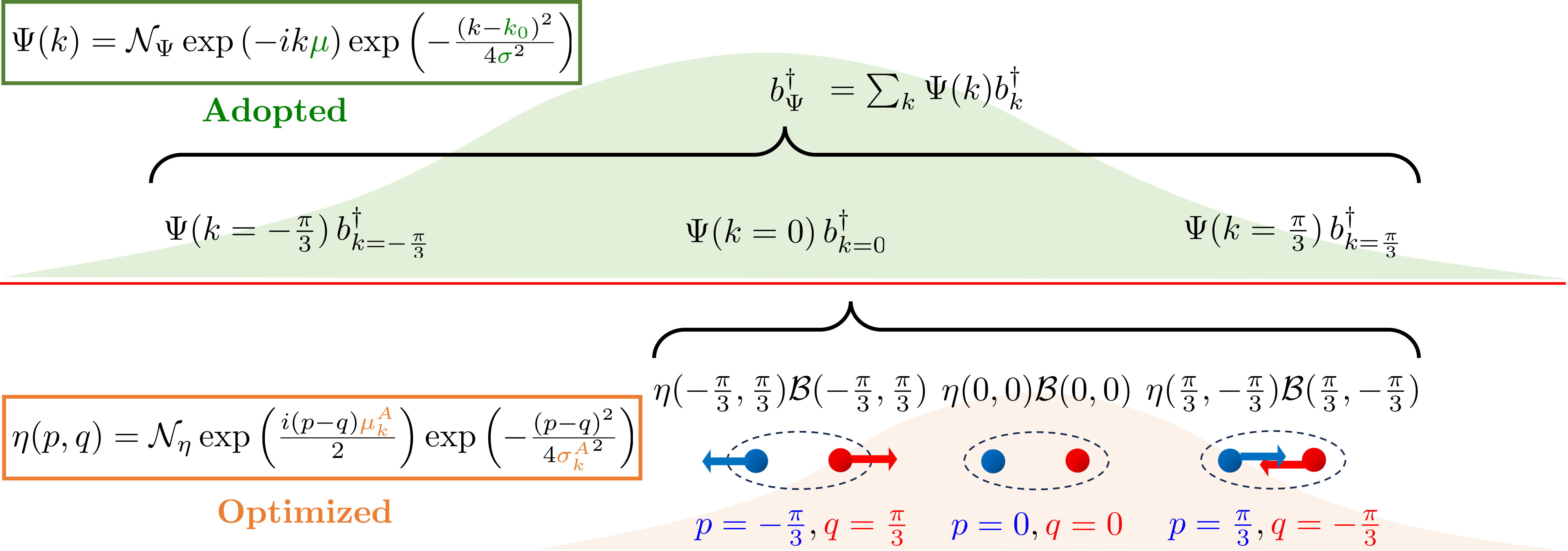
Scattering wave packets of hadrons in gauge theories: Preparation on a quantum computer
Quantum simulation holds promise of enabling a complete description of high-energy scattering processes rooted in gauge theories of the Standard Model. A first step in such simulations is preparation of interacting hadronic wave packets. To create the wave packets, one typically resorts to adiabatic evolution to bridge between wave packets in the free theory and those in the interacting theory, rendering the simulation resource intensive. In this work, we construct a wave-packet creation operator directly in the interacting theory to circumvent adiabatic evolution, taking advantage of resource-efficient schemes for ground-state preparation, such as variational quantum eigensolvers. By means of an ansatz for bound mesonic excitations in confining gauge theories, which is subsequently optimized using classical or quantum methods, we show that interacting mesonic wave packets can be created efficiently and accurately using digital quantum algorithms that we develop. Specifically, we obtain high-fidelity mesonic wave packets in the Z_2 and U(1) lattice gauge theories coupled to fermionic matter in 1+1 dimensions. Our method is applicable to both perturbative and non-perturbative regimes of couplings. The wave-packet creation circuit for the case of the Z_2 lattice gauge theory is built and implemented on the Quantinuum H1-1 trapped-ion quantum computer using 13 qubits and over 300 entangling gates. The fidelities agree well with classical benchmark calculations after employing a simple symmetry-based noise-mitigation technique. This work serves as a step toward quantum computing scattering processes in quantum chromodynamics.
This work is supported, in part, by the DOE QuantISED program through the theory consortium “Intersections of QIS and Theoretical Particle Physics” at Fermilab (Fermilab subcontract no. 666484)
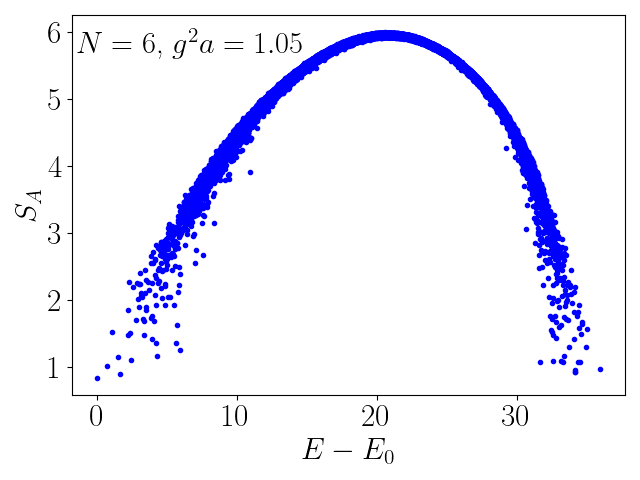
Entanglement Entropy of 2+1-Dimensional SU(2) Lattice Gauge Theory on Plaquette Chains
We study the entanglement entropy of Hamiltonian SU(2) lattice gauge theory in 2+1 dimensions on linear plaquette chains and show that the entanglement entropies of both ground and excited states follow Page curves. The transition of the subsystem size dependence of the entanglement entropy from the area law for the ground state to the volume law for highly excited states is found to be described by a universal crossover function. Quantum many-body scars in the middle of the spectrum, which are present in the electric flux truncated Hilbert space, where the gauge theory can be mapped onto an Ising model, disappear when higher electric field representations are included in the Hilbert space basis. This suggests the continuum 2+1-dimensional SU(2) gauge theory is a “fast” scrambler.
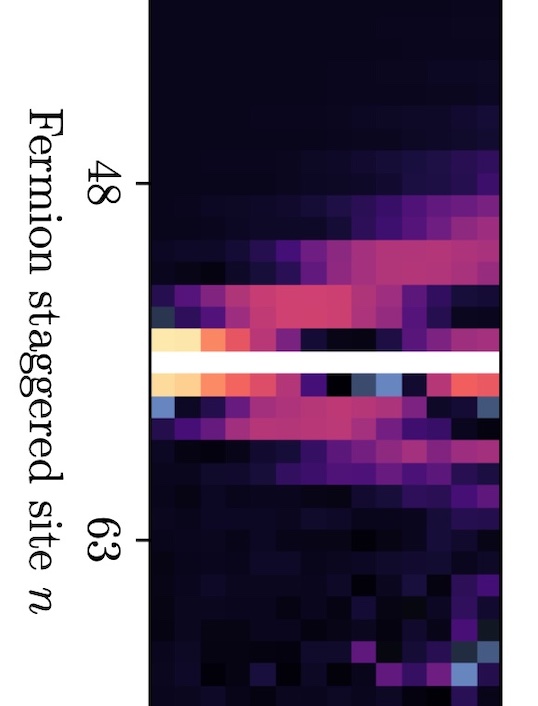
Quantum Simulations of Hadron Dynamics in the Schwinger Model using 112 Qubits
Hadron wavepackets are prepared and time evolved in the Schwinger model using 112 qubits of IBM’s 133-qubit Heron quantum computer ibm_torino. The initialization of the hadron wavepacket is performed in two steps. First, the vacuum is prepared across the whole lattice using the recently developed SC-ADAPT-VQE algorithm and workflow. SC-ADAPT-VQE is then extended to the preparation of localized states, and used to establish a hadron wavepacket on top of the vacuum. This is done by adaptively constructing low-depth circuits that maximize the overlap with an adiabatically prepared hadron wavepacket. Due to the localized nature of the wavepacket, these circuits can be determined on a sequence of small lattices using classical computers, and then robustly scaled to prepare wavepackets on large lattices for simulations using quantum computers. Time evolution is implemented with a second-order Trotterization. To reduce both the required qubit connectivity and circuit depth, an approximate quasi-local interaction is introduced. This approximation is made possible by the emergence of confinement at long distances, and converges exponentially with increasing distance of the interactions. Using multiple error-mitigation strategies, up to 14 Trotter steps of time evolution are performed, employing 13,858 two-qubit gates (with a CNOT depth of 370). The propagation of hadrons is clearly identified, with results that compare favorably with Matrix Product State simulations. Prospectsfor a near-term quantum advantage in simulations of hadron scattering are discussed.
This work was supported, in part, by the U.S. Department of Energy grant DE-FG02-97ER-41014 (Farrell), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS)14 under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Ciavarella, Farrell, Savage), the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (DOE) (Illa), and by the U.S. Department of Energy (DOE), Office of Science under contract DE-AC02-05CH11231, through Quantum Information Science Enabled Discovery (QuantISED) for High Energy Physics (KA2401032) (Ciavarella). This work is also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington. This research used resources of the Oak Ridge Leadership Computing Facility (OLCF), which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725. We acknowledge the use of IBM Quantum services for this work. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team.
Recent Developments in Quarkonium as an Open Quantum System in Quark-Gluon Plasma
We review recent progress in understanding quarkonium dynamics inside the quark-gluon plasma as an open quantum system with a focus on the definition and nonperturbative calculations of relevant transport coefficients and generalized gluon distributions.
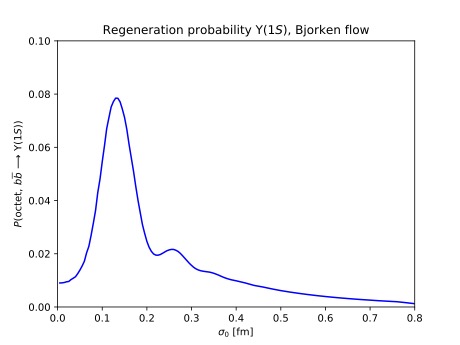
Quarkonium transport in weakly and strongly coupled plasmas
We report on progress in the nonperturbative understanding of quarkonium dynamics inside a thermal plasma. The time evolution of small-size quarkonium is governed by two-point correlation functions of chromoelectric fields dressed with an adjoint Wilson line, known in this context as generalized gluon distributions (GGDs). The GGDs have been calculated in both weakly and strongly coupled plasmas by using perturbative and holographic methods. Strikingly, the results of our calculations for a strongly coupled plasma indicate that the quarkonium dissociation and recombination rates vanish in the transport descriptions that assume quarkonium undergoes Markovian dynamics. However, this does not imply that the dynamics is trivial. As a starting point to explore the phenomenological consequences of the result at strong coupling, we show a calculation of the $\Upsilon(1S)$ formation probability in time-dependent perturbation theory. This is a first step towards the development of a transport formalism that includes non-Markovian effects, which, depending on how close the as of yet undetermined nonperturbative QCD result of the GGDs is to the strongly coupled $\mathcal{N}=4$ SYM result, could very well dominate over the Markovian ones in quark-gluon plasma produced at RHIC and the LHC.
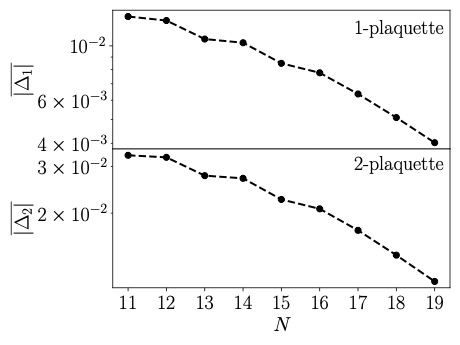
Testing Eigenstate Thermalization Hypothesis for Non-Abelian Gauge Theories
We report on progress in full quantum understanding of thermalization in non-Abelian gauge theories. Specifically, we test the eigenstate thermalization hypothesis for (2+1)-dimensional SU(2) lattice gauge theory.
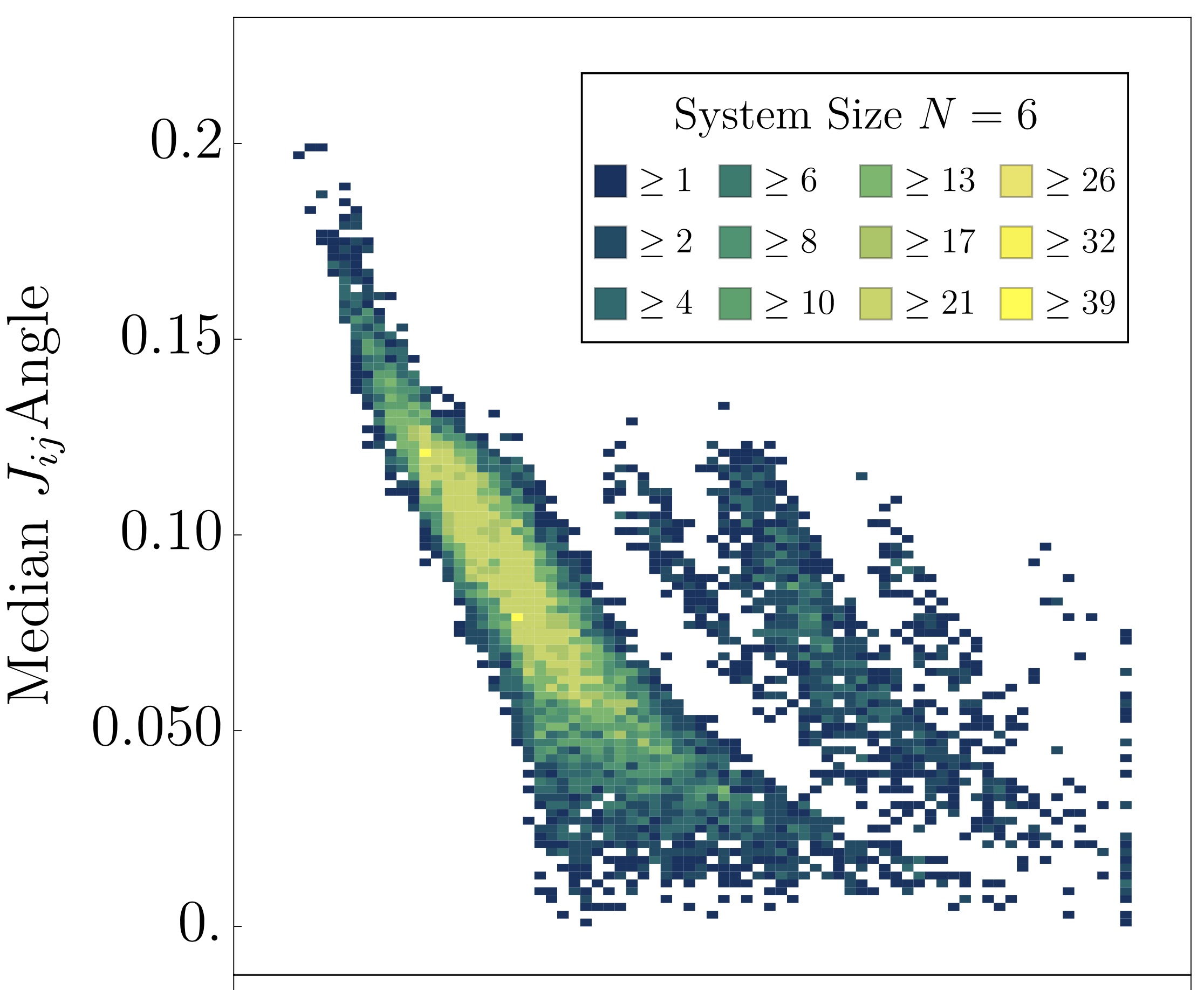
Time Scales in Many-Body Fast Neutrino Flavor Conversion
Time scales associated with many-body fast neutrino flavor conversions in core-collapse supernova are explored in the context of an effective two-flavor “light-bulb” model. We present a preliminary study of time scales obtained from linear stability analyses and from distributions of Loschmidt echo crossing times (intimately connected to dynamical phase transitions) determined by time evolution with the exact many-body Hamiltonian. Starting from a tensor-product initial state describing systems of N neutrinos, with N/2 electron-type and N/2 heavy-type, with uniform distributions of axially-symmetric directions, the Loschmidt echo crossing times are found to exhibit two distinct time scales that are exponentially separated. The second peak structure at longer times, effectively absent for N=4, develops with increasing N. When re-scaled in terms of log t, the distributions are found to become increasingly well described by the sum of two stable distributions. The distribution of Loschmidt echo crossing times differs somewhat from the results of the linear stability analysis, which exhibits a peak at finite frequency and a second peak at zero frequency. The exact analysis suggests that the zero-frequency instability manifests itself as a modest flavor-conversion time scale.
This work was supported in part by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. This work is also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.

Quantum Computing for Nuclear Physics
Future quantum computers are anticipated to be able to perform simulations of quantum many-body systems and quantum field theories that lie beyond the capabilities of classical computation. This will lead to new insights and predictions for systems ranging from dense non equilibrium matter, to low-energy nuclear structure and reactions, to high energy collisions. I present an overview of digital quantum simulations in nuclear physics, with select examples relevant for studies of quark matter.
Conference proceedings for Quark Matter 2023, 3–9 Sept 2023, Houston, Texas, USA.
Generalized Gluon Distribution for Quarkonium Dynamics in Strongly Coupled N=4 Yang-Mills Theory
We study the generalized gluon distribution that governs the dynamics of quarkonium inside a non-Abelian thermal plasma characterizing its dissociation and recombination rates. This gluon distribution can be written in terms of a correlation function of two chromoelectric fields connected by an adjoint Wilson line. We formulate and calculate this object in N=4 supersymmetric Yang-Mills theory at strong coupling using the AdS/CFT correspondence, allowing for a nonzero center-of-mass velocity v of the heavy quark pair relative to the medium. The effect of a moving medium on the dynamics of the heavy quark pair is described by the simple substitution T with Sqrt[gamma] T, in agreement with previous calculations of other observables at strong coupling, where T is the temperature of the plasma in its rest frame, and gamma = (1 – v^2)^{-1/2} is the Lorentz boost factor. Such a velocity dependence can be important when the quarkonium momentum is larger than its mass. Contrary to general expectations for open quantum systems weakly coupled with large thermal environments, the contributions to the transition rates that are usually thought of as the leading ones in Markovian descriptions vanish in this strongly coupled plasma. This calls for new theoretical developments to assess the effects of strongly coupled non-Abelian plasmas on in-medium quarkonium dynamics. Finally, we compare our results with those from weakly coupled QCD, and find that the QCD result moves toward the N=4 strongly coupled result as the coupling constant is increased within the regime of applicability of perturbation theory. This behavior makes it even more pressing to develop a non-Markovian description of quarkonium in-medium dynamics.
Generalized Ginsparg-Wilson relations
We give a general derivation of Ginsparg-Wilson relations for both Dirac and Majorana fermions in any dimension. These relations encode continuous and discrete chiral, parity and time reversal anomalies and will apply to the various classes of free fermion topological insulators and superconductors (in the framework of a relativistic quantum field theory in Euclidian spacetime). We show how to formulate the exact symmetries of the lattice action and the relevant index theorems for the anomalies.
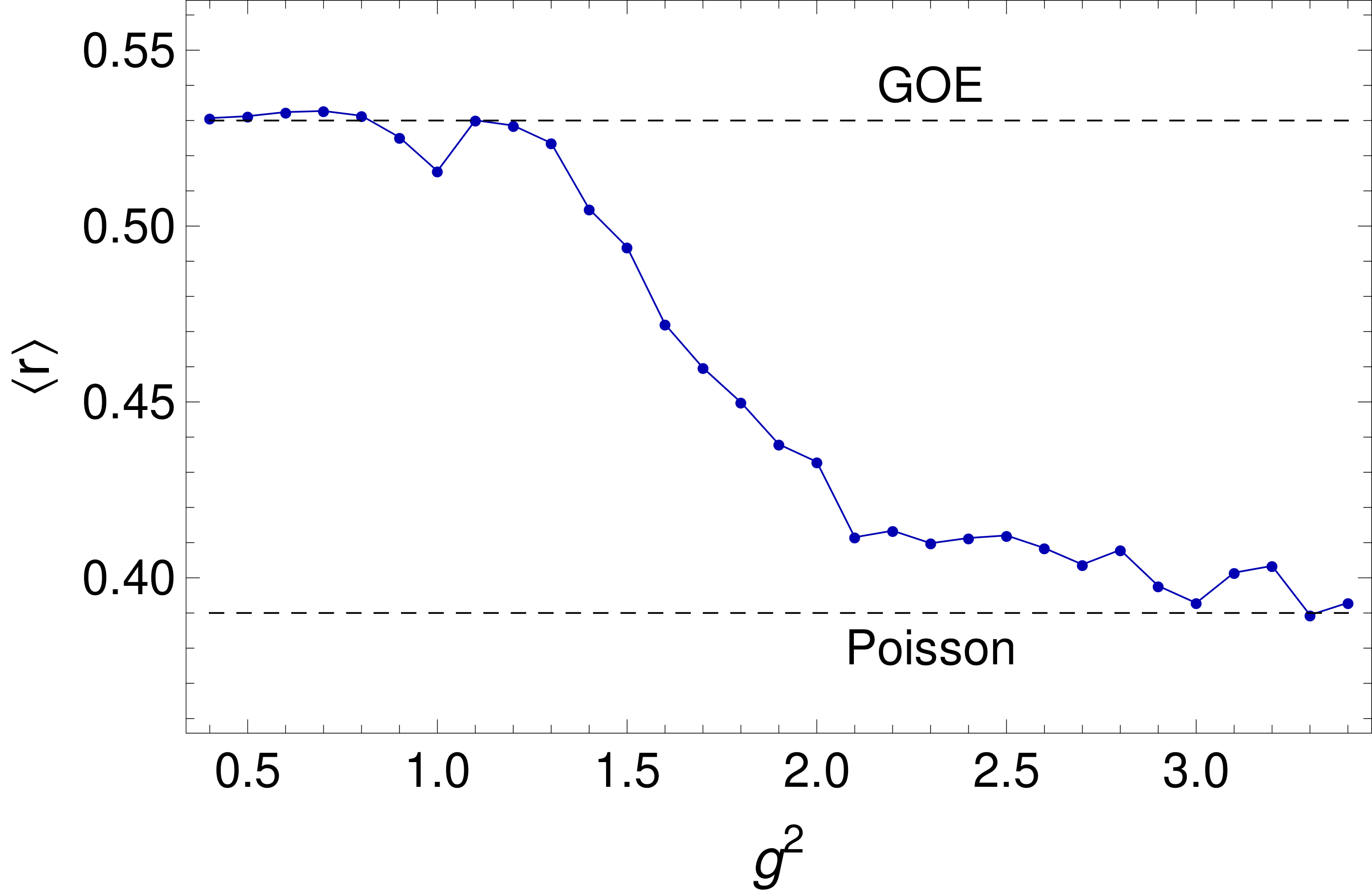
Eigenstate Thermalization in 2+1 dimensional SU(2) Lattice Gauge Theory
We present preliminary numerical evidence for the hypothesis that the Hamiltonian SU(2) gauge theory discretized on a lattice obeys the Eigenstate Thermalization Hypothesis (ETH). To do so we study three approximations: (a) a linear plaquette chain in a reduced Hilbert space limiting the electric field basis to j=0,1/2 , (b) a two-dimensional honeycomb lattice with periodic or closed boundary condition and the same Hilbert space constraint, and (c) a chain of only three plaquettes but such a sufficiently large electric field Hilbert space (j <= 7/2) that convergence of all energy eigenvalues in the analyzed energy window is observed. While an unconstrained Hilbert space is required to reach the continuum limit of SU(2) gauge theory, numerical resource constraints do not permit us to realize this requirement for all values of the coupling constant and large lattices. In each of the three studied cases we check first for RMT behavior and then analyse the diagonal as well as the off-diagonal matrix elements between energy eigenstates for a few operators. Within current uncertainties all results for (b) and (c) agree with ETH predictions while for case (a) deviations are found to be large for one of the analyzed observables. To unambiguously establish ETH behavior and determine for which class of operators it applies, an extension of our investigations is necessary.
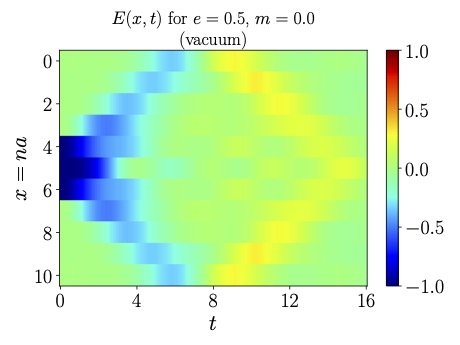
Liouvillian Dynamics of the Open Schwinger Model: String Breaking and Kinetic Dissipation in a Thermal Medium
Understanding the dynamics of bound state formation is one of the fundamental questions in confining quantum field theories such as Quantum Chromodynamics (QCD). One hadronization mechanism that has garnered significant attention is the breaking of a string initially connecting a fermion and an anti-fermion. Deepening our understanding of real-time string-breaking dynamics with simpler, lower dimensional models like the Schwinger model can improve our understanding of the hadronization process in QCD and other confining systems found in condensed matter and statistical systems. In this paper, we consider the string-breaking dynamics within the Schwinger model and investigate its modification inside a thermal medium, treating the Schwinger model as an open quantum system coupled to a thermal environment. Within the regime of weak coupling between the system and environment, the real-time evolution of the system can be described by a Lindblad evolution equation. We analyze the Liouvillian gaps of this Lindblad equation and the time dependence of the system’s von Neumann entropy. We observe that the late-time relaxation rate decreases as the environment correlation length increases. Moreover, when the environment correlation length is infinite, the system exhibits two steady states, one in each of the sectors with definite charge-conjugation-parity (CP) quantum numbers. For parameter regimes where an initial string breaks in vacuum, we observe a delay of the string breaking in the medium, due to kinetic dissipation effects. Conversely, in regimes where an initial string remains intact in vacuum time evolution, we observe string breaking (melting) in the thermal medium. We further discuss how the Liouvillian dynamics of the open Schwinger model can be simulated on quantum computers and provide an estimate of the associated Trotter errors.
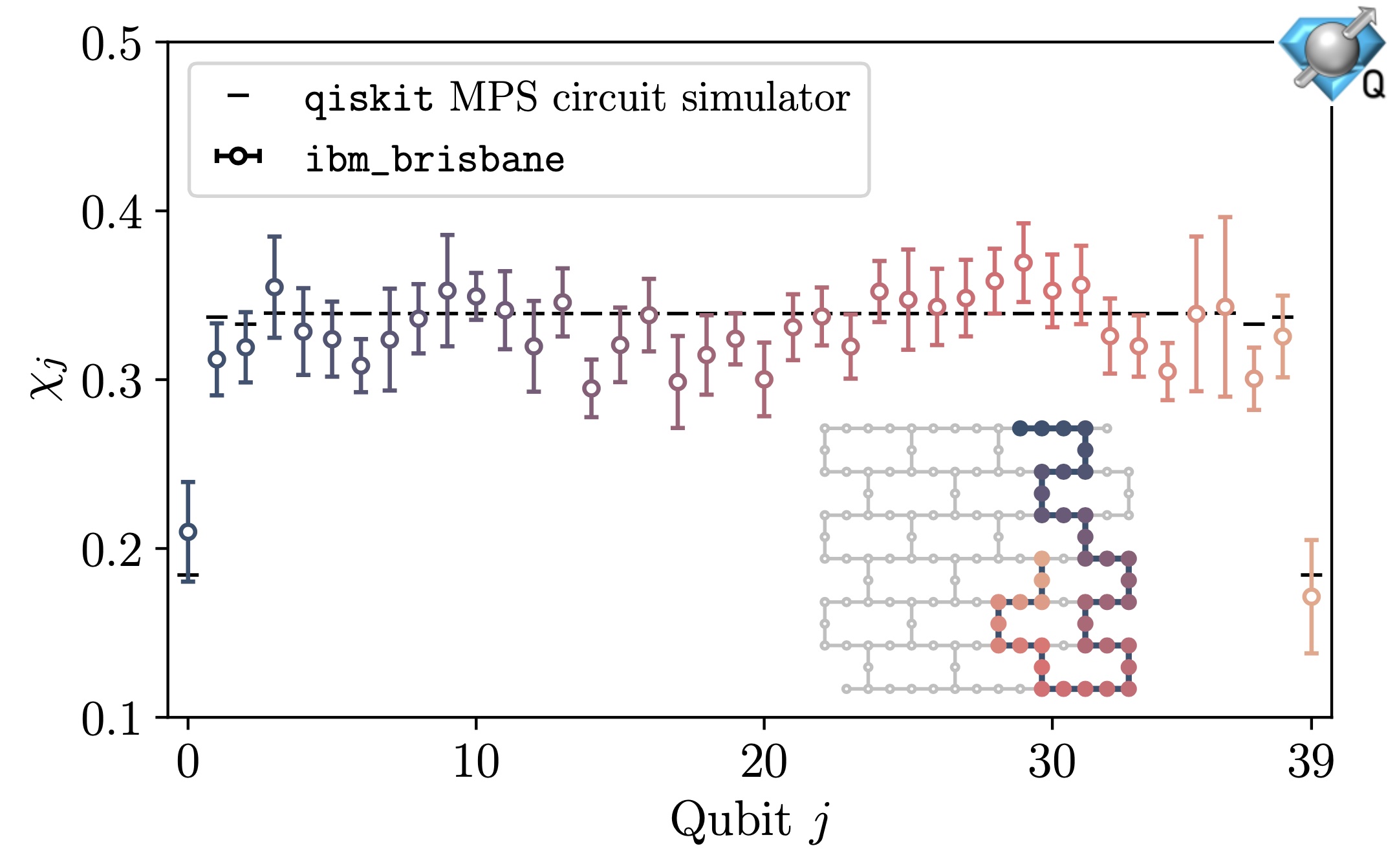
Scalable Circuits for Preparing Ground States on Digital Quantum Computers: The Schwinger Model Vacuum on 100 Qubits
The vacuum of the lattice Schwinger model is prepared on up to 100 qubits of IBM’s Eagle-processor quantum computers. A new algorithm to prepare the ground state of a gapped translationally-invariant system on a quantum computer is presented, which we call Scalable Circuits ADAPT-VQE (SC ADAPT-VQE). This algorithm uses the exponential decay of correlations between distant regions of the ground state, together with ADAPT-VQE, to construct quantum circuits for state preparation that can be scaled to arbitrarily large systems. SC-ADAPT-VQE is applied to the Schwinger model, and shown to be systematically improvable, with an accuracy that converges exponentially with circuit depth. Both the structure of the circuits and the deviations of prepared wavefunctions are found to become independent of the number of spatial sites, L. This allows for a controlled extrapolation of the circuits, determined using small or modest-sized systems, to arbitrarily large L. The circuits for the Schwinger model are determined on lattices up to L=14 (28 qubits) with the qiskit classical simulator, and subsequently scaled up to prepare the L=50 (100 qubits) vacuum on IBM’s 127 superconducting-qubit quantum computers ibm_brisbane and ibm_cusco . After applying an improved error-mitigation technique, which we call Operator Decoherence Renormalization, the chiral condensate and charge-charge correlators obtained from the quantum computers are found to be in good agreement with classical Matrix Product State simulations.
This work was supported, in part, by the U.S. Department of Energy grant DE-FG02-97ER-41014 (Farrell), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Ciavarella, Farrell, Savage), and the Quantum Science Center (QSC), a National Quantum Information Science Research Center of the U.S. Department of Energy (DOE) (Illa). This work was also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.
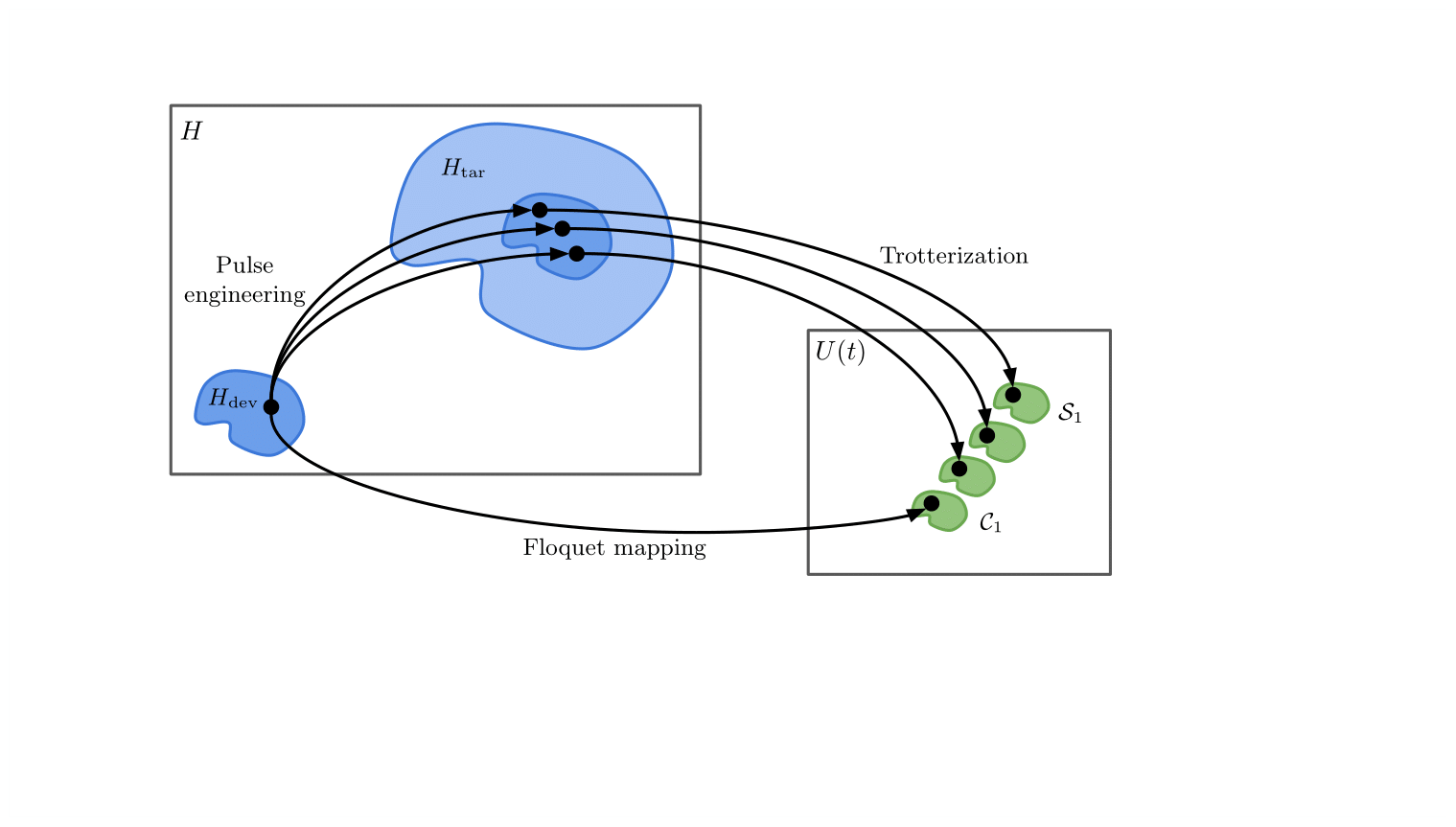
Optimization of Algorithmic Errors in Analog Quantum Simulations
Analog quantum simulation is emerging as a powerful tool for uncovering classically unreachable physics such as many-body real-time dynamics. We study a class of errors for approximate time evolution algorithms in Heisenberg-type systems on analog quantum devices described by the Ising Hamiltonian. A general framework for quantifying these errors is introduced and applied to several proposed time evolution methods, including Trotter-like methods and Floquet-engineered constant-field approaches. This analysis explains the interplay of different error sources arising from approximations to the propagator of a physical theory. The limitations placed on the accuracy of time evolution methods by current devices are discussed. Characterization of the error scaling provides a way to extend the presented Hamiltonian engineering methods to take advantage of forthcoming device capabilities.
A new basis for Hamiltonian SU(2) simulations
Due to rapidly improving quantum computing hardware, Hamiltonian simulations of relativistic lattice field theories have seen a resurgence of attention. This computational tool requires turning the formally infinite-dimensional Hilbert space of the full theory into a finite-dimensional one. For gauge theories, a widely-used basis for the Hilbert space relies on the representations induced by the underlying gauge group, with a truncation that keeps only a set of the lowest dimensional representations. This works well at large bare gauge coupling, but becomes less efficient at small coupling, which is required for the continuum limit of the lattice theory. In this work, we develop a new basis suitable for the simulation of an SU(2) lattice gauge theory in the maximal tree gauge. In particular, we show how to perform a Hamiltonian truncation so that the eigenvalues of both the magnetic and electric gauge-fixed Hamiltonian are mostly preserved, which allows for this basis to be used at all values of the coupling. Little prior knowledge is assumed, so this may also be used as an introduction to the subject of Hamiltonian formulations of lattice gauge theories.
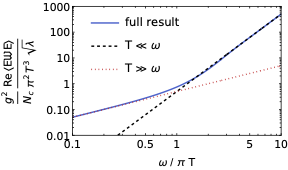
Quarkonium transport in strongly coupled plasmas
Suppression of open heavy flavors and quarkonia in heavy-ion collisions is among the most informative probes of the quark-gluon plasma. Interpreting the full wealth of data obtained from the collision events requires a precise understanding of the evolution of heavy quarks and quarkonia as they propagate through the nearly thermal and strongly coupled plasma. Systematic theoretical studies of quarkonium time evolution in the QGP in the regime where the temperature of the QGP is much smaller than the inverse of quarkonium size have only been carried out in the past few years.
Such calculations require the evaluation of a gauge-invariant correlator of chromoelectric fields dressed with Wilson lines, which is similar to, but different from, the correlation used to define the well-known heavy quark diffusion coefficient. The origin of this difference has been explained previously. Here we show a calculation of the analogous correlator in strongly coupled N=4 SYM using the AdS/CFT correspondence at a finite temperature. While it resembles the open heavy quark case, it has some crucial differences that highlight the relevance of quantum color correlations. We will also discuss the results for the quarkonium transport coefficients obtained from this correlator, thereby establishing the first analytic results at strong coupling in this context.
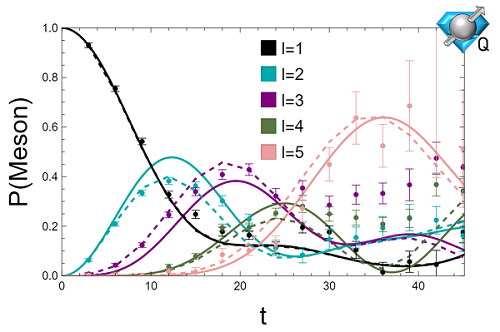
Quantum Simulation of Lattice QCD with Improved Hamiltonians
Quantum simulations of lattice gauge theories are anticipated to directly probe the real time dynamics of QCD, but scale unfavorably with the required truncation of the gauge fields. Improved Hamiltonians are derived to correct for the effects of gauge field truncations on the SU(3) Kogut-Susskind Hamiltonian. It is shown in 1+1D that this enables low chromo-electric field truncations to quantitatively reproduce features of the untruncated theory over a range of couplings and quark masses. In 3+1D, an improved Hamiltonian is derived for lattice QCD with staggered massless fermions. It is shown in the strong coupling limit that the spectrum qualitatively reproduces aspects of two flavor QCD and simulations of a small system are performed on IBM’s Perth quantum processor.
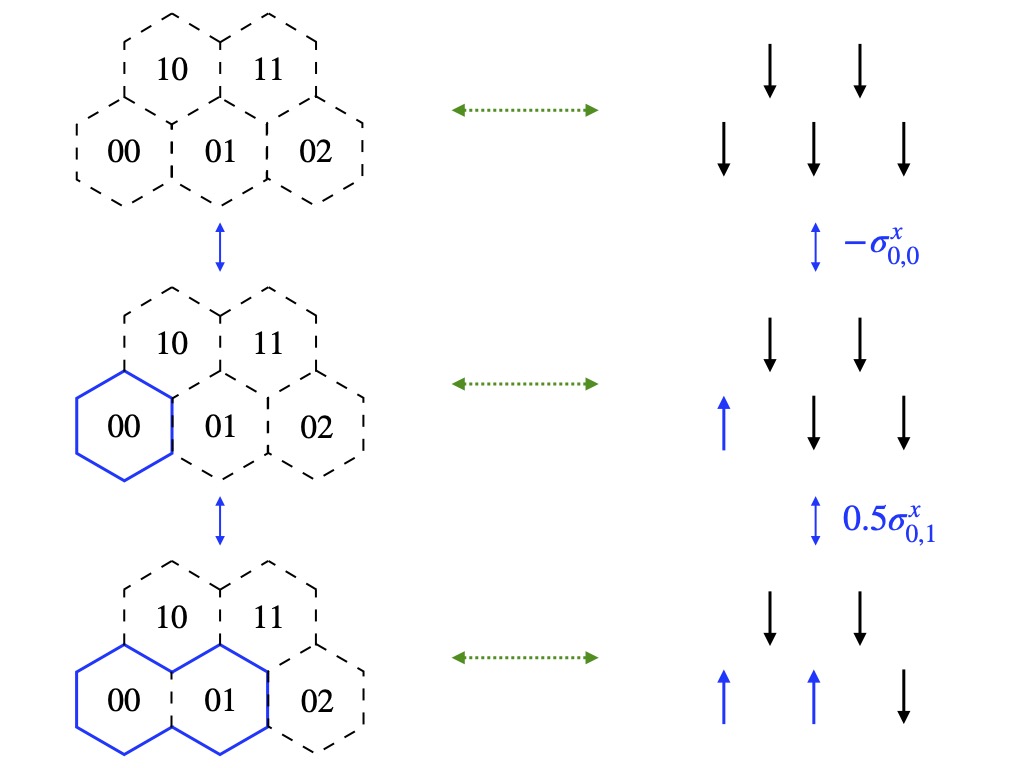
Simple Hamiltonian for Quantum Simulation of Strongly Coupled 2+1D SU(2) Lattice Gauge Theory on a Honeycomb Lattice
We find a simple spin Hamiltonian to describe physical states of 2+1D SU(2) lattice gauge theory on a honeycomb lattice with a truncation of the electric field representation at j_max=1/2. The simple spin Hamiltonian only contains local products of Pauli matrices, even though Gauss’s law has been completely integrated out.
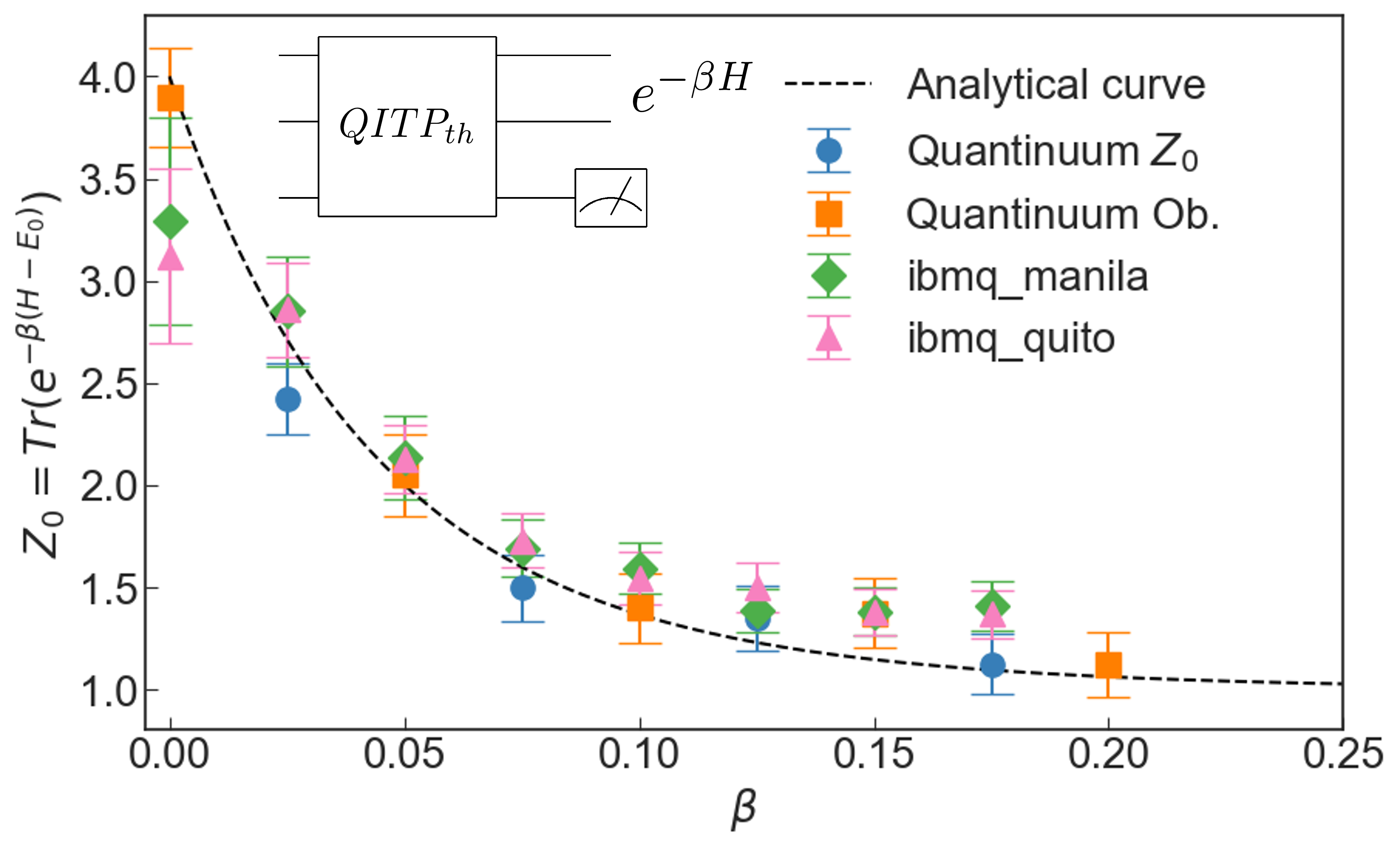
Quantum Imaginary Time Propagation algorithm for preparing thermal states
Calculations at finite temperatures are fundamental in different scientific fields, from nuclear physics to condensed matter. Evolution in imaginary time is a prominent classical technique for preparing thermal states of quantum systems. We propose a new quantum algorithm that prepares thermal states based on the quantum imaginary time propagation method, using a diluted operator with ancilla qubits to overcome the non-unitarity nature of the imaginary time operator. The presented method is the first that allows us to obtain the correct thermal density matrix on a general quantum processors for a generic Hamiltonian. We prove its reliability in the actual quantum hardware computing thermal properties for two and three neutron systems.
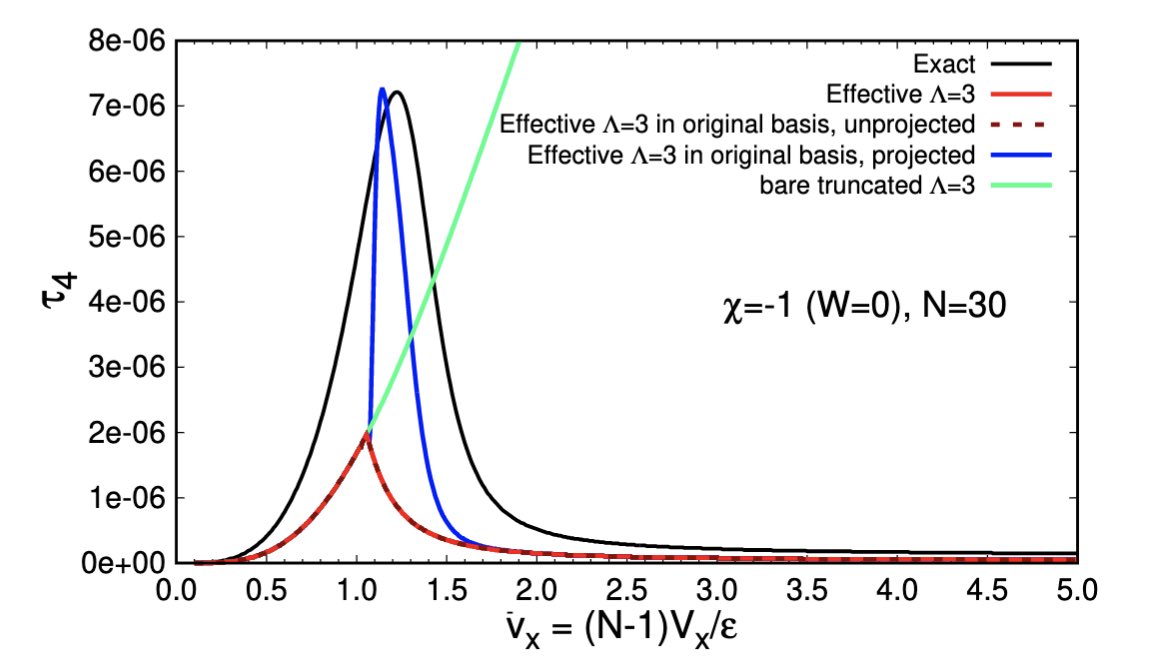
Multi-Body Entanglement and Information Rearrangement in Nuclear Many-Body Systems
The present work examines how effective-model-space calculations of nuclear many-body systems are able to rearrange and converge multi-particle entanglement, and information more generally. The generalized Lipkin-Meshkov-Glick (LMG) model is considered here as a demonstration, to motivate and provide insight for future developments of entanglement-driven descriptions of nuclei. The effective approach is based on a truncation of the Hilbert space to an effective model space, together with a variational rotation of the qubits (spins), which constitute the relevant elementary degrees of freedom in this model. The non-commutivity of the rotation and truncation allow for an exponential improvement of the energy convergence throughout much of the model space, compared with truncations without rotations, as we have shown previously in the reduced LMG model. Our analysis is extended to examine measures of correlations and entanglement, and to quantify their convergence with increasing cut-off. We focus on one- and two-spin entanglement entropies, mutual information, as well as n-tangles for n=2, 4 to estimate multi-body entanglement. The effective description is found to provide “minimal” entropies and mutual information of the rotated spins, while, at the same time, being able to recover the exact results to a large extent with low cut-offs. Naive truncations of the bare Hamiltonian, on the other hand, artificially underestimate these measures. The n-tangles in the present model provide a basis-independent measures of n-particle entanglement. While these are found to be more difficult to capture with the EMS description, the improvement in convergence, compared to truncations of the bare Hamiltonian, is significantly more dramatic. Finally, we investigate how spin squeezing, which is particularly sensitive to entanglement details of the system, is reproduced by quantum simulations of the LMG model we previously performed using IBM’s quantum computers. We conclude that the low-energy effective model space techniques, that successfully provide predictive capabilities for low-lying observables in many-body systems, exhibit analogous efficacy for quantum correlations and multi-body entanglement in the LMG model, motivating future studies in nuclear many-body systems that are closer to nature. We anticipate our results have import for effective field theories relevant to high-energy physics and nuclear physics more broadly.
This work was supported, in part, by Universit ̈at Bielefeld and ERC- 885281-KILONOVA Advanced Grant, and, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science.
Quantum simulation of fundamental particles and forces
Key static and dynamic properties of matter — from creation in the Big Bang to evolution into subatomic and astrophysical environments — arise from the underlying fundamental quantum fields of the standard model and their effective descriptions. However, the simulation of these properties lies beyond the capabilities of classical computation alone. Advances in quantum technologies have improved control over quantum entanglement and coherence to the point at which robust simulations of quantum fields are anticipated in the foreseeable future. In this Perspective article, we discuss the emerging area of quantum simulations of standard-model physics, outlining the challenges and opportunities for progress in the context of nuclear and high-energy physics.
Real Time Quarkonium Transport Coefficients in Open Quantum Systems from Euclidean QCD
Recent open quantum system studies showed that quarkonium time evolution inside the quark-gluon plasma is determined by transport coefficients that are defined in terms of a gauge invariant correlator of two chromoelectric field operators connected by an adjoint Wilson line. We study the Euclidean version of the correlator for quarkonium evolution and discuss the extraction of the transport coefficients from this Euclidean correlator, highlighting its difference from other problems that also require reconstructing a spectral function, such as the calculation of the heavy quark diffusion coefficient. Along the way, we explain why the transport coefficient gamma(adj) differs from gamma(fund) at finite temperature at O(g^4), in spite of the fact that their corresponding spectral functions differ only by a temperature-independent term at the same order. We then discuss how to evaluate the Euclidean correlator via lattice QCD methods, with a focus on reducing the uncertainty caused by infrared renormalons in determining the renormalization factor nonperturbatively.
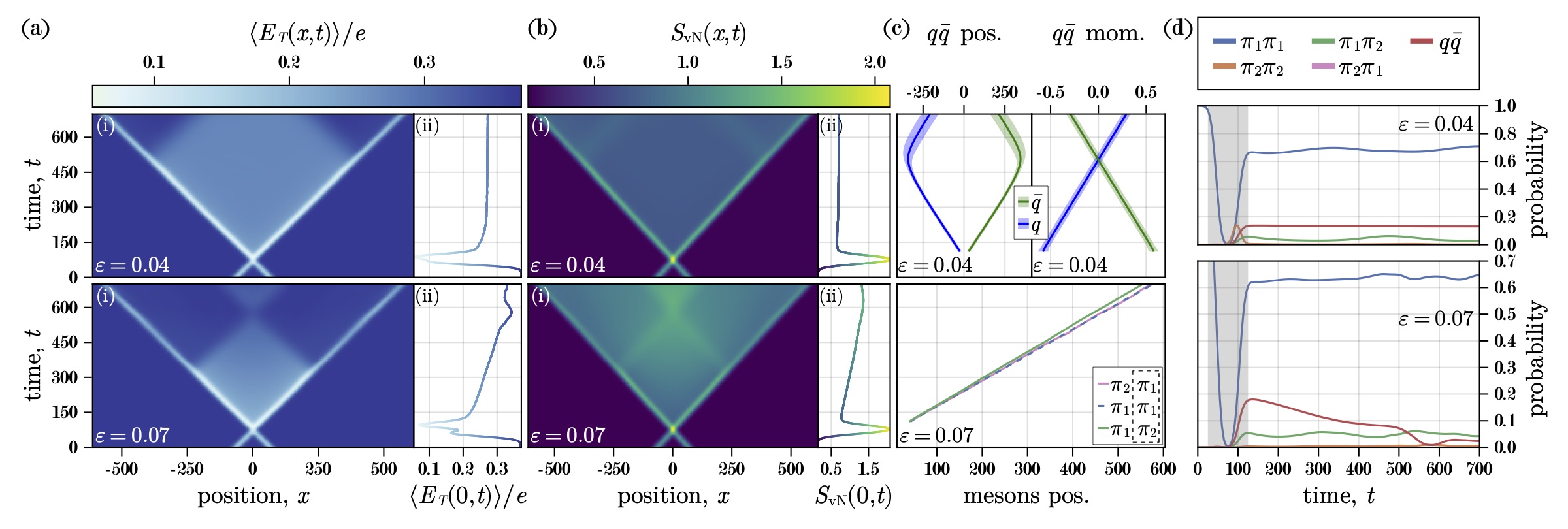
High-energy Collision of Quarks and Hadrons in the Schwinger Model: From Tensor-Networks to Circuit-QED
With the aim of studying nonperturbative, out-of-equilibrium dynamics of high-energy particle collisions on quantum simulators, we investigate the scattering dynamics of lattice quantum electrodynamics in 1+1 dimensions. Working in the bosonized formulation of the model, an analog circuit-QED implementation is proposed that is native to the platform, hence requires minimal ingredients and approximations, and enables practical schemes for particle wavepacket preparation and evolution. Furthermore, working in the thermodynamic limit, uniform-matrix-product-state tensor networks are used to construct multi-particle wavepacket states, evolve them in time, and detect outgoing particles post collision. This facilitates the numerical simulation of scattering experiments in both confined and deconfined regimes of the model at different energies, giving rise to rich phenomenology, including inelastic production of quark and meson states, meson disintegration, and dynamical string formation and breaking. Elastic and inelastic scattering cross sections are obtained, together with time-resolved momentum and position distributions of the outgoing particles. This study highlights the role of classical and quantum simulation in enhancing our understanding of scattering processes in quantum field theories in real time.
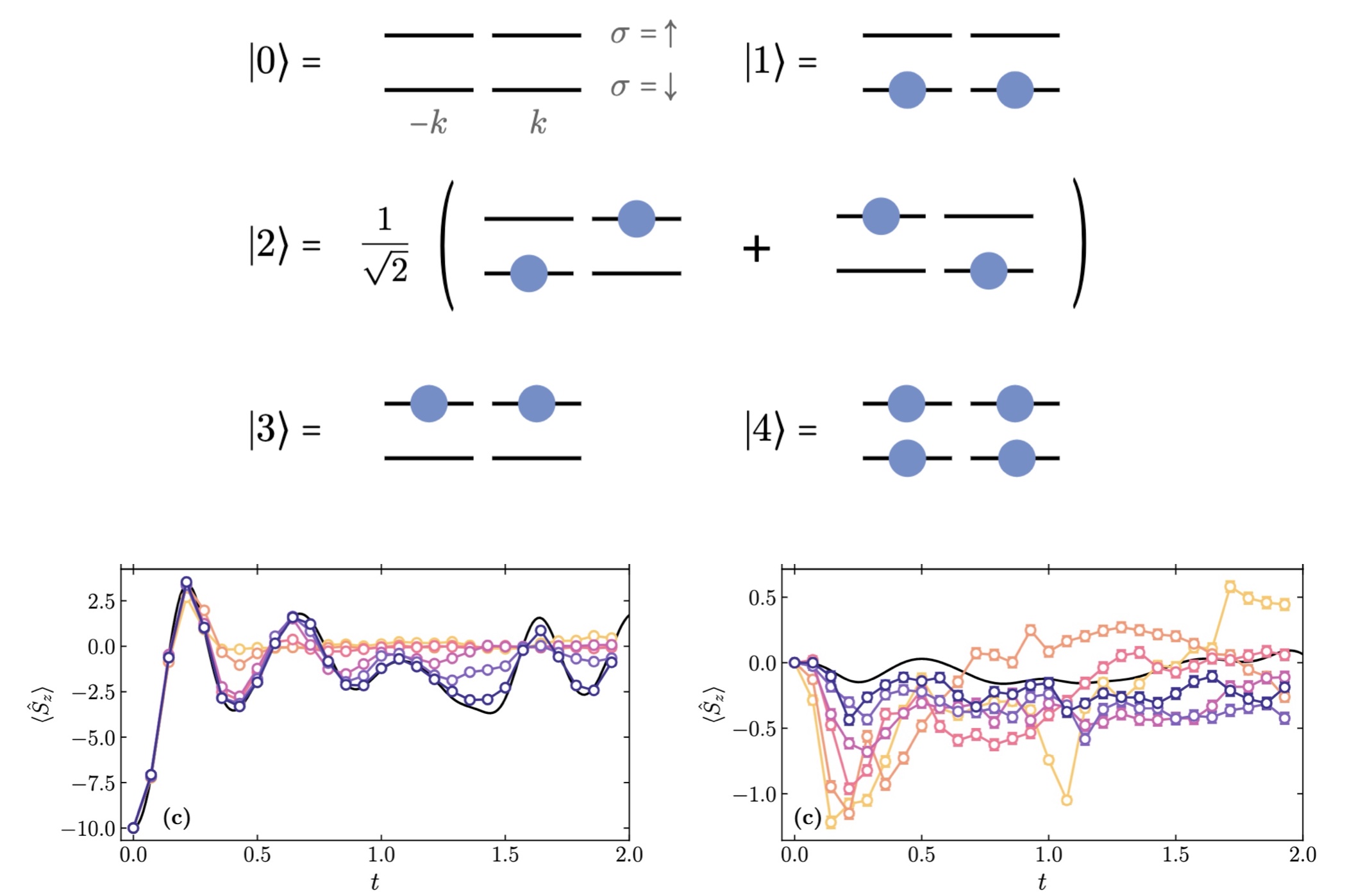
Quantum Simulations of SO(5) Many-Fermion Systems using Qudits
The structure and dynamics of many-body systems are the result of a delicate interplay between underlying interactions. Fermionic pairing plays a central role in various physical systems and can lead to collective phenomena such as superconductivity and superfluidity. We explore the potential utility of quantum computers with arrays of qudits in simulating interacting fermionic systems, when the qudits can be naturally mapped to the relevant degrees of freedom. The Agassi model of fermions is based on an underlying $so(5)$ algebra, and the systems it describes can be partitioned into pairs of modes with five basis states, which naturally embed in arrays of $d=5$ qudits (qu5its). Classical noiseless simulations of the time evolution of systems of fermions embedded in up to twelve qu5its are performed using Google’s {\tt cirq} software. The resource requirements of the qu5it circuits are analyzed and compared with two different mappings to qubit systems, a physics-aware Jordan-Wigner mapping and a state-to- state mapping. We find advantages in using qudits, specifically in lowering the required quantum resources and reducing anticipated errors that take the simulation out of the physical space. A previously unrecognized sign problem has been identified from Trotterization errors in time evolving high-energy excitations. This has implications for quantum simulations in high energy and nuclear physics, specifically of fragmentation and highly inelastic, multi-channel processes.
This work was supported, in part, by Universität Bielefeld and ERC- 885281-KILONOVA Advanced Grant (Robin), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 (Savage), and the Quantum Science Center (QSC), a National Quantum Information Science Research Center of the U.S. Department of Energy (Illa).
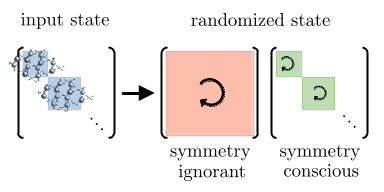
Randomized measurement protocols for lattice gauge theories
Randomized measurement protocols, including classical shadows, entanglement tomography, and randomized benchmarking are powerful techniques to estimate observables, perform state tomography, or extract the entanglement properties of quantum states. While unraveling the intricate structure of quantum states is generally difficult and resource-intensive, quantum systems in nature are often tightly constrained by symmetries. This can be leveraged by the symmetry-conscious randomized measurement schemes we propose, yielding clear advantages over symmetry-blind randomization such as reducing measurement costs, enabling symmetry-based error mitigation in experiments, allowing differentiated measurement of (lattice) gauge theory entanglement structure, and, potentially, the verification of topologically ordered states in existing and near-term experiments. Crucially, unlike symmetry-blind randomized measurement protocols, these latter tasks can be performed without relearning symmetries via full reconstruction of the density matrix.
Chromoelectric field correlator for quarkonium transport in the strongly coupled N=4 Yang-Mills plasma from AdS/CFT
Previous studies have shown that a gauge-invariant correlation function of two chromoelectric fields connected by a straight timelike adjoint Wilson line encodes crucial information about quark-gluon plasma (QGP) that determines the dynamics of small-sized quarkonium in the medium. Motivated by the successes of holographic calculations to describe strongly coupled QGP, we calculate the analog gauge-invariant correlation function in strongly coupled $\mathcal{N}=4$ supersymmetric Yang-Mills theory at finite temperature by using the AdS/CFT correspondence. Our results indicate that the transition processes between bound and unbound quarkonium states are suppressed in strongly coupled plasmas, and moreover, the leading contributions to these transition processes vanish in both the quantum Brownian motion and quantum optical limits of open quantum system approaches to quarkonia.
SU(2) Non-Abelian Gauge Theory on a Plaquette Chain Obeys Eigenstate Thermalization Hypothesis
We test the eigenstate thermalization hypothesis (ETH) for 2+1 dimensional SU(2) lattice gauge theory. By considering the theory on a chain of plaquettes and truncating basis states for link variables at j=1/2, we can map it onto an Ising chain and numerically exactly diagonalize the Hamiltonian for reasonably large lattice sizes. We find energy level repulsion in momentum sectors with no remaining discrete symmetries. We study two local observables made up of Wilson loops and calculate their matrix elements in the energy eigenbasis, which are shown consistent with the ETH. Our study implies a subset of states in the physical Hilbert space of Quantum Chromodynamics (QCD) obeys the ETH.

White paper on Quantum Information Science and Technology for Nuclear Physics. Input into U.S. Long-Range Planning, 2023.
In preparation for the 2023 NSAC Long Range Plan (LRP), members of the Nuclear Science community gathered to discuss the current state of, and plans for further leveraging opportunities in, QIST in NP research at the Quantum Information Science for U.S. Nuclear Physics Long Range Planning workshop [4], held in Santa Fe, New Mexico on January 31—Feb 1, 2023. The workshop, jointly-sponsored by Los Alamos National Laboratory (LANL) and the InQubator for Quantum Simulation (IQuS), included 45 in-person participants and 53 remote attendees. The outcome of the workshop identified strategic plans and requirements for the next 5-10 years to advance quantum sensing and quantum simulations within NP, and to develop a diverse quantum-ready workforce. The plans include resolutions endorsed by the participants to address the compelling scientific opportunities at the intersections of NP and QIST. These endorsements are aligned with similar affirmations by the LRP Computational Nuclear Physics and AI/ML Workshop, the Nuclear Structure, Reactions, and Astrophysics LRP Town Hall, and the Fundamental Symmetries, Neutrons, and Neutrinos LRP Town Hall communities.
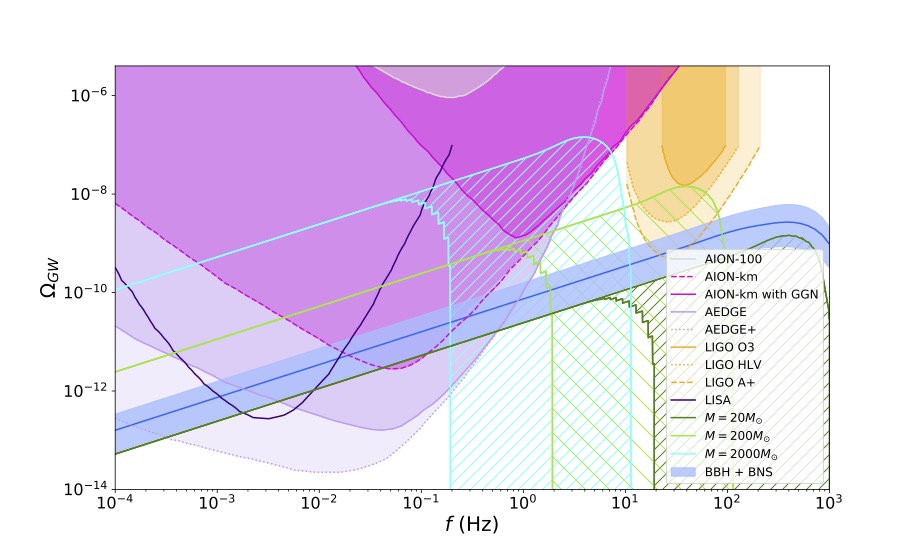
Gravitational Wave Backgrounds from Colliding ECOs
Long baseline atom interferometers offer an exciting opportunity to explore mid-frequency gravitational waves. In this work we survey the landscape of possible contributions to the total “gravitational wave background” in this frequency band and advocate for targeting this observable. Such an approach is complimentary to searches for resolved mergers from individual sources and may have much to reveal about the Universe. We find that the inspiral phases of stellar-mass compact binaries cumulatively produce a signal well within reach of the proposed AION-km and AEDGE experiments. Hypothetical populations of dark sector exotic compact objects, harbouring just a tiny fraction of the dark energy density, could also generate signatures unique to mid- and low-frequency gravitational wave detectors, providing a novel means to probe complexity in the dark sector.

Demonstration of a quantum-classical coprocessing protocol for simulating nuclear reactions
Quantum computers hold great promise for arriving at exact simulations of nuclear dynamical processes (e.g., scattering and reactions) that are paramount to the study of nuclear matter at the limit of stability and to explaining the formation of chemical elements in stars. However, quantum simulations of the unitary (real) time dynamics of fermionic many-body systems require a currently prohibitive number of reliable and long-lived qubits. We propose a co-processing algorithm for the simulation of real-time dynamics in which the time evolution of the spatial coordinates is carried out on a classical processor, while the evolution of the spin degrees of freedom is carried out on a quantum processor. This hybrid algorithm is demonstrated in a quantum simulation of the scattering of two neutrons performed on the Lawrence Berkeley National Laboratory’s Advanced Quantum Testbed. We show that, after implementation of error mitigation strategies to improve the accuracy of the algorithm in addition to the use of either circuit compression techniques or tomography as methods to elucidate the onset of decoherence, this initial demonstration validates the principle of the proposed co-processing scheme. We anticipate that a generalization of this present scheme will open the way for (real-time) path integral simulations of nuclear scattering.
This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. This work was prepared in part by LLNL under Contract No. DE-AC52-07NA27344 with support from the Laboratory Directed Research and Development Grant No. 19-DR- 005, and it was funded in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics (under Work Proposal No. SCW1730), the Office of Advanced Scientific Computing Research Quantum Testbed Program (under Work Proposal No. FP00008338), and the Department of Energy National Nuclear Security Ad- ministration, Advanced Simulation and Computing Program.
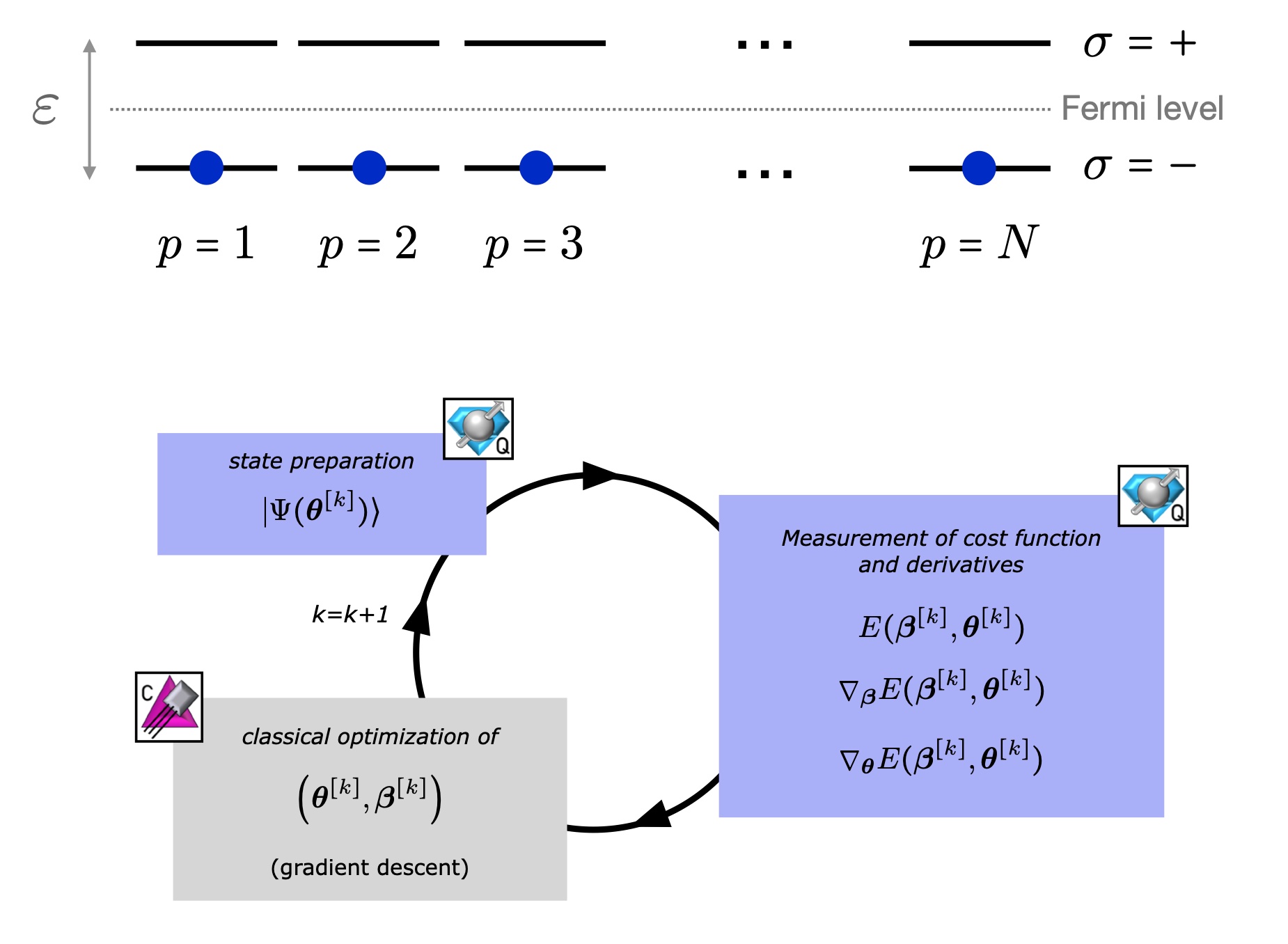
Quantum Simulations in Effective Model Spaces (I): Hamiltonian Learning-VQE using Digital Quantum Computers and Application to the Lipkin-Meshkov-Glick Model
The utility of effective model spaces in quantum simulations of non-relativistic quantum many-body systems is explored in the context of the Lipkin-Meshkov-Glick model of interacting fermions. We introduce an iterative hybrid-classical-quantum algorithm, Hamiltonian learning variational quantum eigensolver (HL-VQE), that simultaneously optimizes an effective Hamiltonian, thereby rearranging entanglement into the effective model space, and the associated ground-state wavefunction. HL-VQE is found to provide an exponential improvement in Lipkin-Meshkov-Glick model calculations, compared to a naive truncation without Hamiltonian learning, throughout a significant fraction of the Hilbert space. Quantum simulations are performed to demonstrate the HL-VQE algorithm, using an efficient mapping where the number of qubits scales with the log of the size of the effective model space, rather than the particle number, allowing for the description of large systems with small quantum circuits. Implementations on IBM’s QExperience quantum computers and simulators for 1- and 2-qubit effective model spaces are shown to provide accurate and precise results, reproducing classical predictions. This work constitutes a step in the development of entanglement-driven quantum algorithms for the description of nuclear systems, that leverages the potential of noisy intermediate-scale quantum (NISQ) devices.
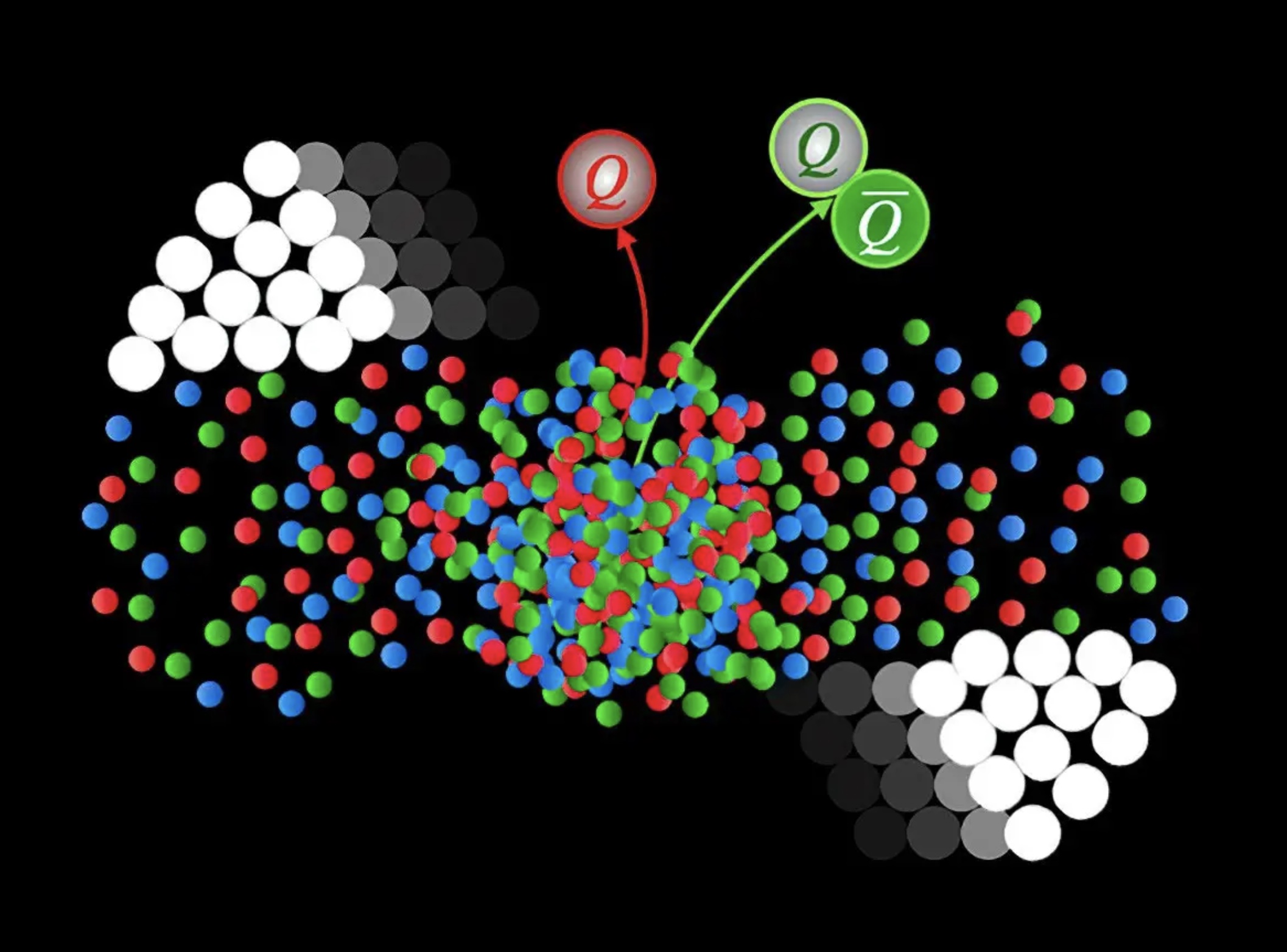
Gauge Invariance of Non-Abelian Field Strength Correlators: the Axial Gauge Puzzle
Many transport coefficients of the quark-gluon plasma and nuclear structure functions can be written as gauge invariant correlation functions of non-Abelian field strengths dressed with Wilson lines. We discuss the applicability of axial gauge n.A=0 to calculate them. In particular, we address issues that appear when one attempts to trivialize the Wilson lines in the correlation functions by gauge-fixing. We find it is always impossible to completely remove the gauge fields n.A in Wilson lines that extend to infinity in the n-direction by means of gauge transformations. We show how the obstruction appears in an explicit example of a perturbative calculation, and we also explain it more generally from the perspective of the path integral that defines the theory. Our results explain why the two correlators that define the heavy quark and quarkonium transport coefficients, which are seemingly equal in axial gauge, are actually different physical quantities of the quark-gluon plasma and have different values. Furthermore, our findings provide insights into the difference between two inequivalent gluon parton distribution functions.
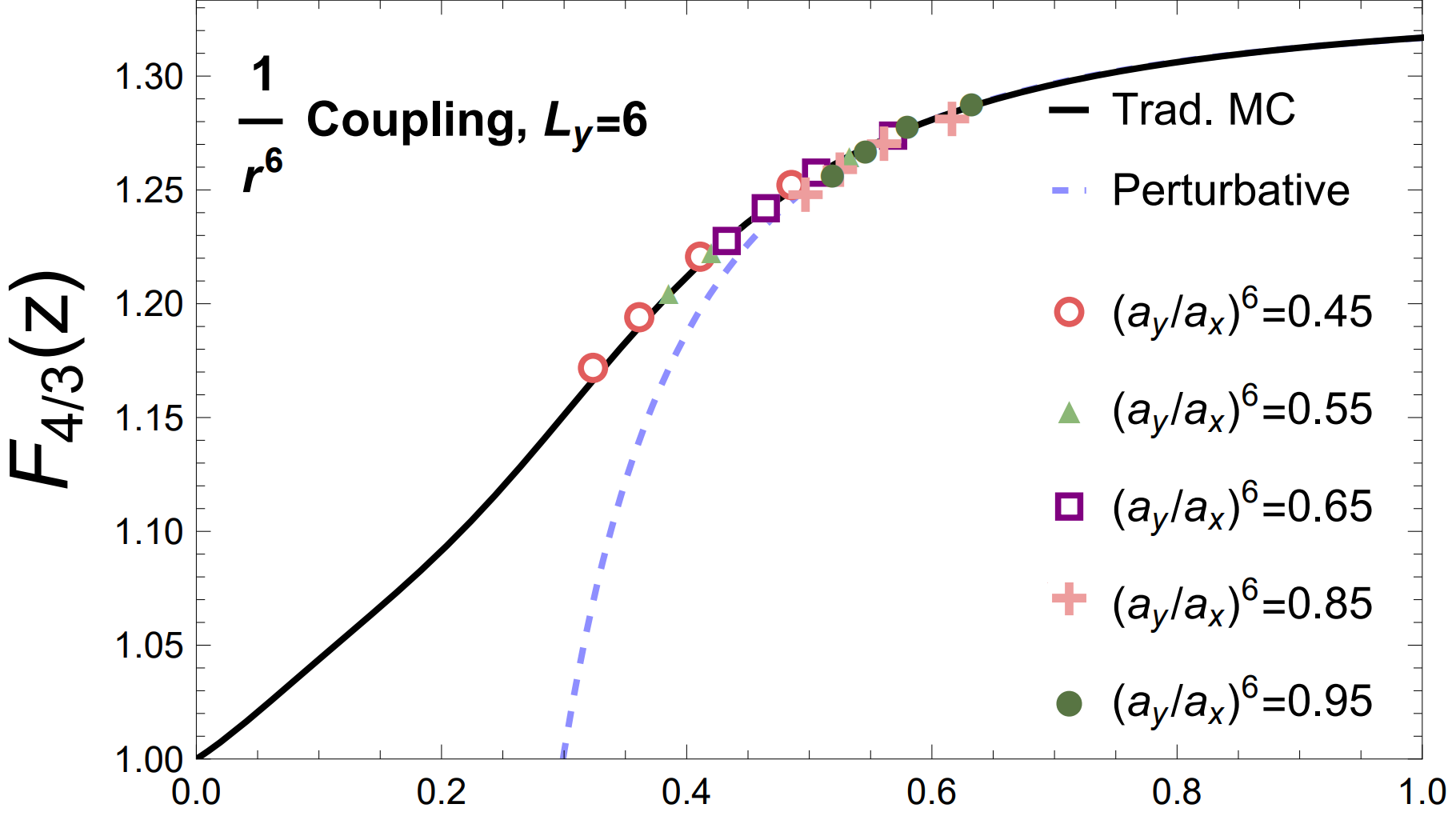
Preparation for Quantum Simulation of the 1+1D O(3) Non-linear σ-Model using Cold Atoms
The 1+1D O(3) non-linear σ-model is a model system for future quantum lattice simulations of other
asymptotically-free theories, such as non-Abelian gauge theories. We find that utilizing dimensional reduction
can make efficient use of two-dimensional layouts presently available on cold atom quantum simulators. A
new definition of the renormalized coupling is introduced, which is applicable to systems with open boundary
conditions and can be measured using analog quantum simulators. Monte Carlo and tensor network calculations
are performed to determine the quantum resources required to reproduce perturbative short-distance observables.
In particular, we show that a rectangular array of 48 Rydberg atoms with existing quantum hardware capabilities
should be able to adiabatically prepare low-energy states of the perturbatively-matched theory. These states can
then be used to simulate non-perturbative observables in the continuum limit that lie beyond the reach of classical
computers.
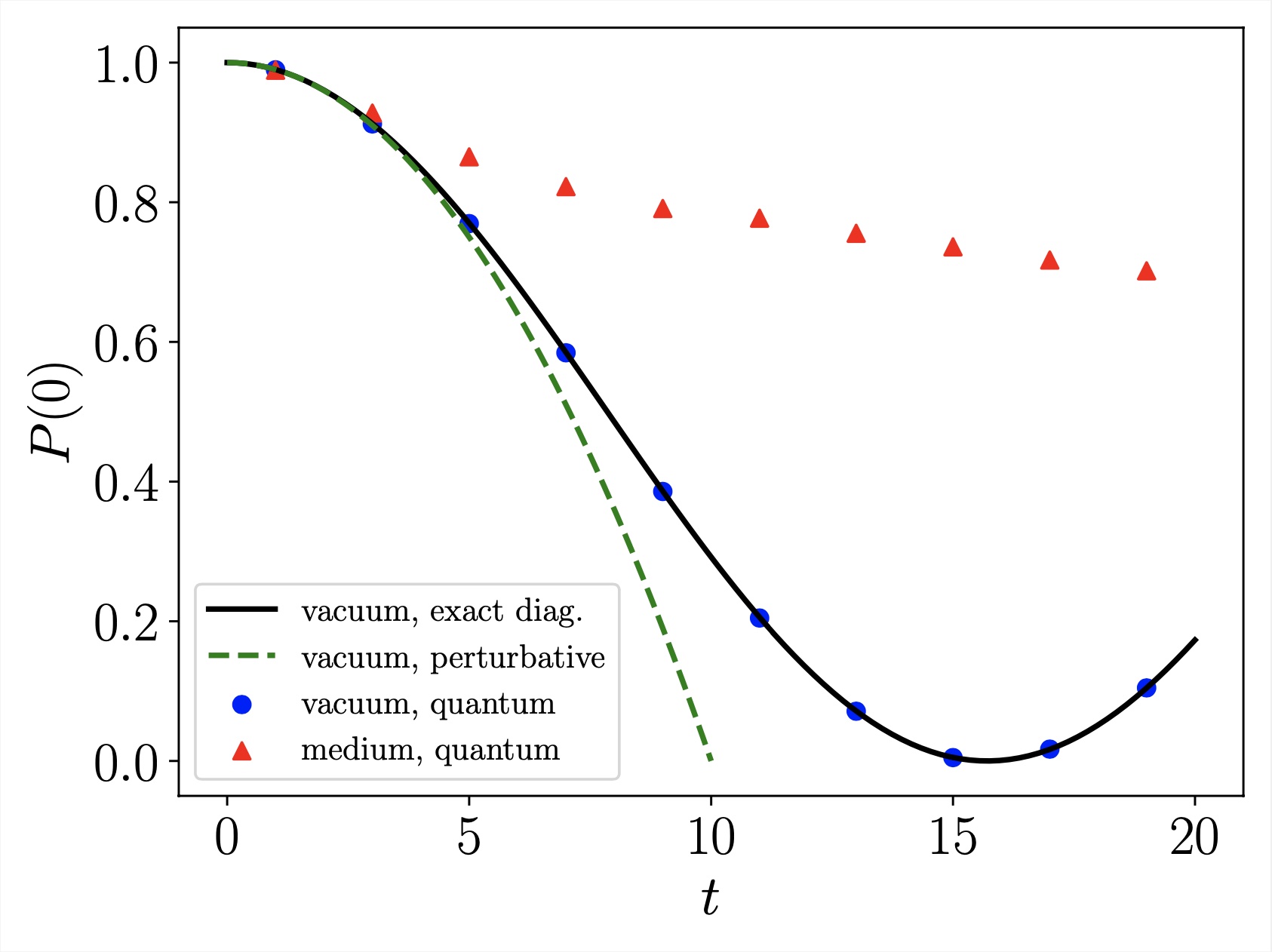
Quantum Simulation of Light-Front QCD for Jet Quenching in Nuclear Environments
We develop a framework to simulate jet quenching in nuclear environments on a quantum computer. The formulation is based on the light-front Hamiltonian dynamics of QCD. The Hamiltonian consists of three parts relevant for jet quenching studies: kinetic, diffusion and splitting terms. In the basis made up of $n$-particle states in momentum space, the kinetic Hamiltonian is diagonal. Matrices representing the diffusion and splitting parts are sparse. The diffusion part of the Hamiltonian depends on classical background gauge fields, which need to be sampled classically before constructing quantum circuits for the time evolution. The cost of the sampling scales linearly with the time length of the evolution and the momentum grid volume. The framework automatically keeps track of quantum interference and thus it can be applied to study the Landau-Pomeranchuk-Migdal effect in cases with more than two splittings, which is beyond the scope of state-of-the-art analyses, no matter whether the medium is static or expanding, thin or thick, hot or cold. We apply this framework to study a toy model and gluon in-medium radiation on a small lattice. The Landau-Pomeranchuk-Migdal effect that suppresses the total radiation probability is observed in the quantum simulation results of both the toy model and the gluon case.
Faster spectral density calculation using energy moments
Accurate predictions of inclusive scattering cross sections in the linear response regime require efficient and controllable methods to calculate the spectral density in a strongly-correlated many-body system. In this work we reformulate the recently proposed Gaussian Integral Transform technique in terms of Fourier moments of the system Hamiltonian which can be computed efficiently on a quantum computer. One of the main advantages of this framework is that it allows for an important reduction of the computational cost by exploiting previous knowledge about the energy moments of the spectral density. For a simple model of medium mass nucleus like ⁴⁰Ca and target energy resolution of 1 MeV we find an expected speed-up of ≈ 125 times for the calculation of the giant dipole response and of ≈ 50 times for the simulation of quasi-elastic electron scattering at typical momentum transfers.
Multi-Neutrino Entanglement and Correlations in Dense Neutrino Systems
The time-evolution of multi-neutrino entanglement and correlations are studied in two-flavor collective neutrino oscillations, relevant for dense neutrino environments, building upon previous works. Specifically, simulations performed of systems with up to 12 neutrinos using Quantinuum’s H1-1 20 qubit trapped-ion quantum computer are used to compute n-tangles, and two- and three-body correlations, probing beyond mean-field descriptions. n-tangle re-scalings are found to converge for large system sizes.
This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https:// iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 (Savage), and the Quantum Science Center (QSC) (https://qscience.org), a National Quantum Information Science Research Center of the U.S. Department of Energy (DOE) (Illa). This work is also supported, in part, through the Department of Physics (https://phys.washington.edu) and the College of Arts and Sciences (https://www.artsci.washington. edu) at the University of Washington. This research used resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725.
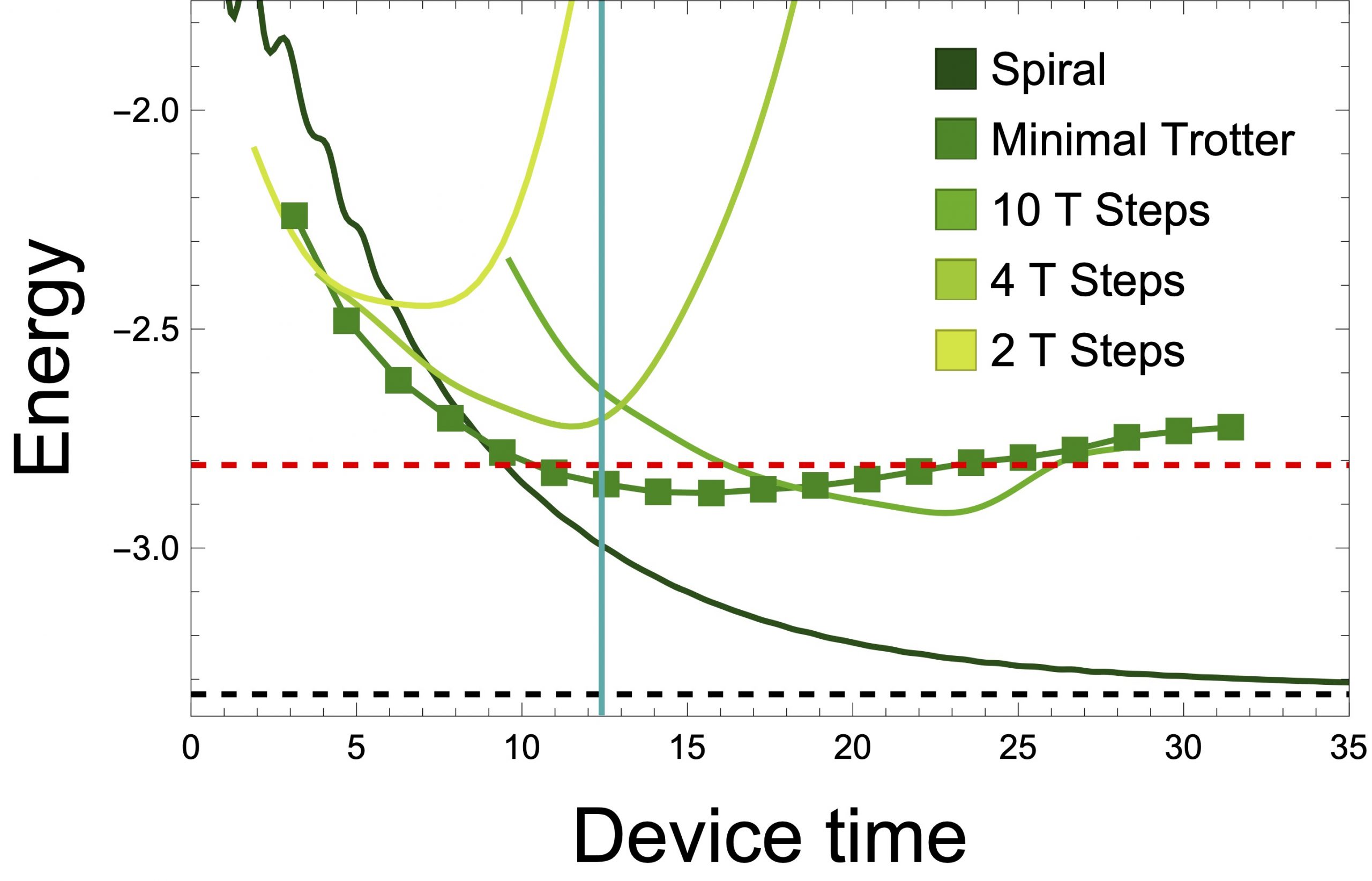
State Preparation in the Heisenberg Model through Adiabatic Spiraling
An adiabatic state preparation technique, called the adiabatic spiral, is proposed for the Heisenberg model. This technique is suitable for implementation on a number of quantum simulation platforms such as Rydberg atoms, trapped ions, or superconducting qubits. Classical simulations of small systems suggest that it can be successfully implemented in the near future. A comparison to Trotterized time evolution is performed and it is shown that the adiabatic spiral is able to outperform Trotterized adiabatics.
The material presented here was funded in part by the DOE QuantISED program through the theory consortium “Intersections of QIS and Theoretical Particle Physics” at Fermilab with Fermilab Subcontract No. 666484, and in part by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE- SC0020970 and the Quantum Science Center (QSC) a National Quantum Information Science Research Center of the U.S. Department of Energy.
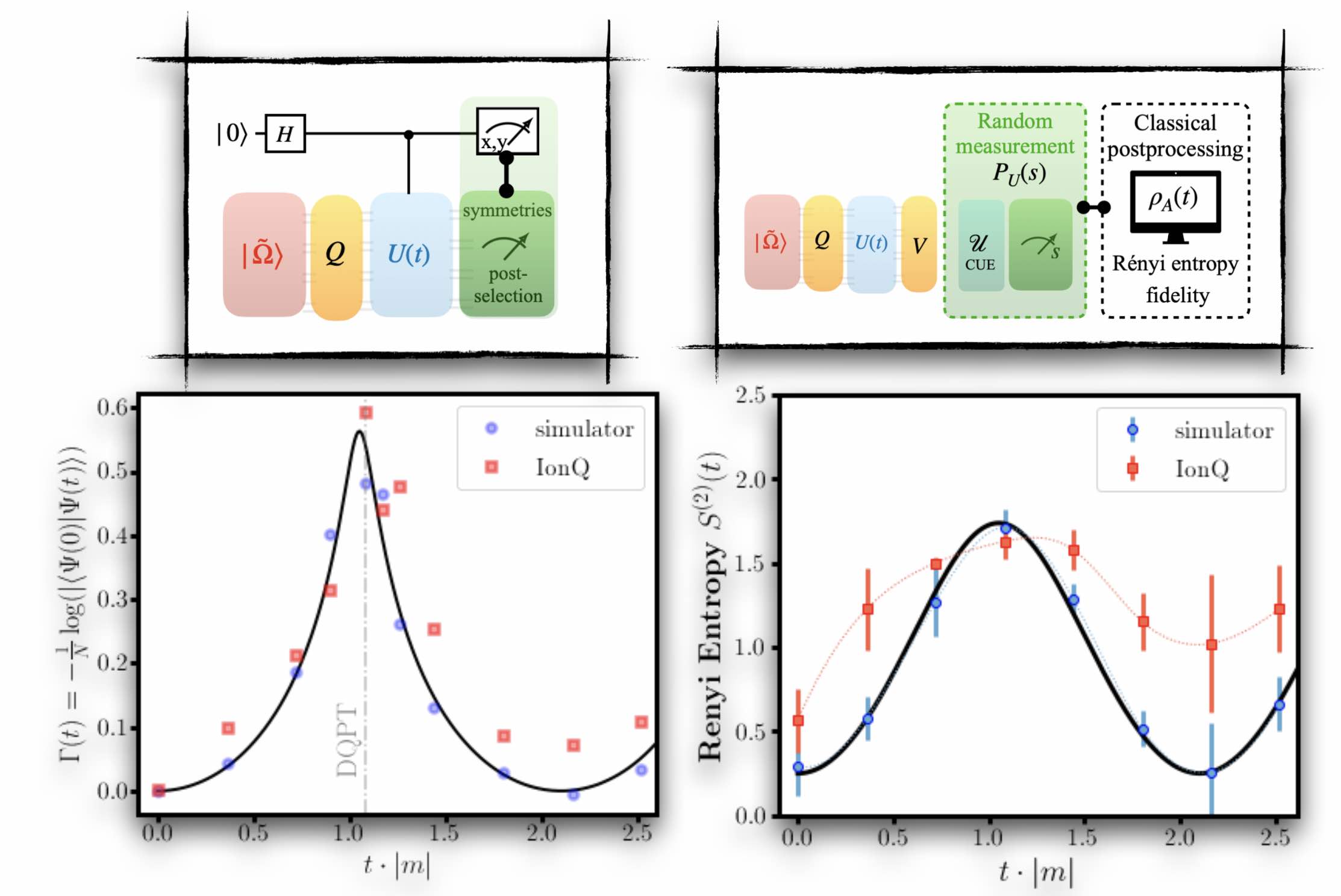
Quantum computation of dynamical quantum phase transitions and entanglement tomography in a lattice gauge theory
Strongly-coupled gauge theories far from equilibrium may exhibit unique features that could illuminate the physics of early universe and of hadron and ion colliders. Studying real-time phenomena has proven challenging with classical-simulation methods, but is a natural application of quantum-simulation devices. To demonstrate this prospect, we quantum compute non-equal time correlation functions and perform entanglement tomography of non-equilibrium states of a simple lattice gauge theory, the Schwinger model, using a trapped-ion quantum computer by IonQ Inc. As an ideal target for near-term devices, a recently-predicted dynamical quantum phase transition in this model is studied by preparing, quenching, and tracking the subsequent non-equilibrium dynamics in three ways: i) overlap echos signaling dynamical transitions, ii) non-equal time correlation functions with an underlying topological nature, and iii) the entanglement structure of non-equilibrium states, including Entanglement Hamiltonians. These results constitute the first observation of a dynamical quantum phase transition in a lattice gauge theory on a quantum computer, and are a first step toward investigating topological phenomena in nuclear and high-energy physics using quantum technologies.
Lattice regularization of Theta-vacua in Grassmannian nonlinear sigma models: Anomalies, sign-problems and qubit models
Anomalies are a powerful way to gain insight into possible lattice regularizations of a quantum field theory. In this work, we consider lattice regularizations of a class of the toy-models of QCD: the 1+1-dimensional asymptotically-free Grassmanian nonlinear sigma models with a theta term. We argue that the continuum anomaly for a given symmetry can be matched by a manifestly symmetric lattice regularization only if (i) the symmetry action is offsite, or (ii) if the continuum anomaly is reproduced exactly on the lattice. Using the Grassmanian nonlinear sigma models as a case study, we provide examples of lattice regularizations in which both possibilities are realized. For possibility (i), we generalize recent work for the O(3) NLSM with an arbitrary theta term, where it was regulated using model of qubits with a small extra dimension, solving a sign problem present in conventional formulations of theta vacua. We argue that Grassmannian NLSM can be obtained similarly from SU(N) antiferromagnets with a well-defined continuum limit, reproducing both the IR physics of theta vacua and the UV physics of asymptotic freedom. These results enable the application of new classical algorithms to lattice Monte Carlo studies of these quantum field theories, and provide a viable realization suited for their quantum simulation. On the other hand, we show that, perhaps surprisingly, the conventional lattice regularization of theta vacua due to Berg and Luscher reproduces the anomaly exactly on the lattice, providing a realization of the second possibility.
Preparations for Quantum Simulations of Quantum Chromodynamics in 1+1 Dimensions: (II) Single-Baryon Beta-Decay in Real Time
A framework for quantum simulations of real-time weak decays of hadrons and nuclei in a 2-flavor lattice theory in one spatial dimension is presented. A single generation of the Standard Model is mapped to spin operators via the Jordan-Wigner transformation, and both quantum chromodynamics and flavor-changing weak interactions are included in the dynamics, the latter through four-Fermi effective operators. This mapping requires 16 qubits per spatial lattice site. Quantum circuits which implement time evolution in this lattice theory are developed and run on Quantinuum’s H1 1 20-qubit trapped ion system to simulate the beta-decay of a single baryon on one lattice site. Simulations of the real-time evolution of a single baryon, including initial state preparation, are performed for both one and two Trotter time steps. We comment on the potential intrinsic error-correction properties of this type of lattice theory.
Branching States as The Emergent Structure of a Quantum Universe
Quantum Darwinism builds on decoherence theory to explain the emergence of classical behavior within a quantum universe. We demonstrate that the differential geometric underpinnings of quantum mechanics provide a uniquely informative window into the structure of correlations needed to validate quantum Darwinism. This leads us to two crucial insights about the emergence of classical phenomenology, centered around the nullity of quantum discord. First, we show that the so-called branching structure of the joint state of system and environment is the only one compatible with zero discord. Second, we prove that for small, but nonzero discord, the structure of the globally pure state is arbitrarily close to the branching form. These provide strong evidence that this class of branching states is the only one compatible with the emergence of classical phenomenology, as described in quantum Darwinism.
Simulating Heisenberg interactions in the Ising model with strong drive fields
The time-evolution of an Ising model with large driving fields over discrete time intervals is shown to be reproduced by an effective XXZ-Heisenberg model at leading order in the inverse field strength. For specific orientations of the drive field, the dynamics of the XXX-Heisenberg model is reproduced. These approximate equivalences, valid above a critical driving field strength set by dynamical phase transitions in the Ising model, are expected to enable quantum devices that natively evolve qubits according to the Ising model to simulate more complex systems.
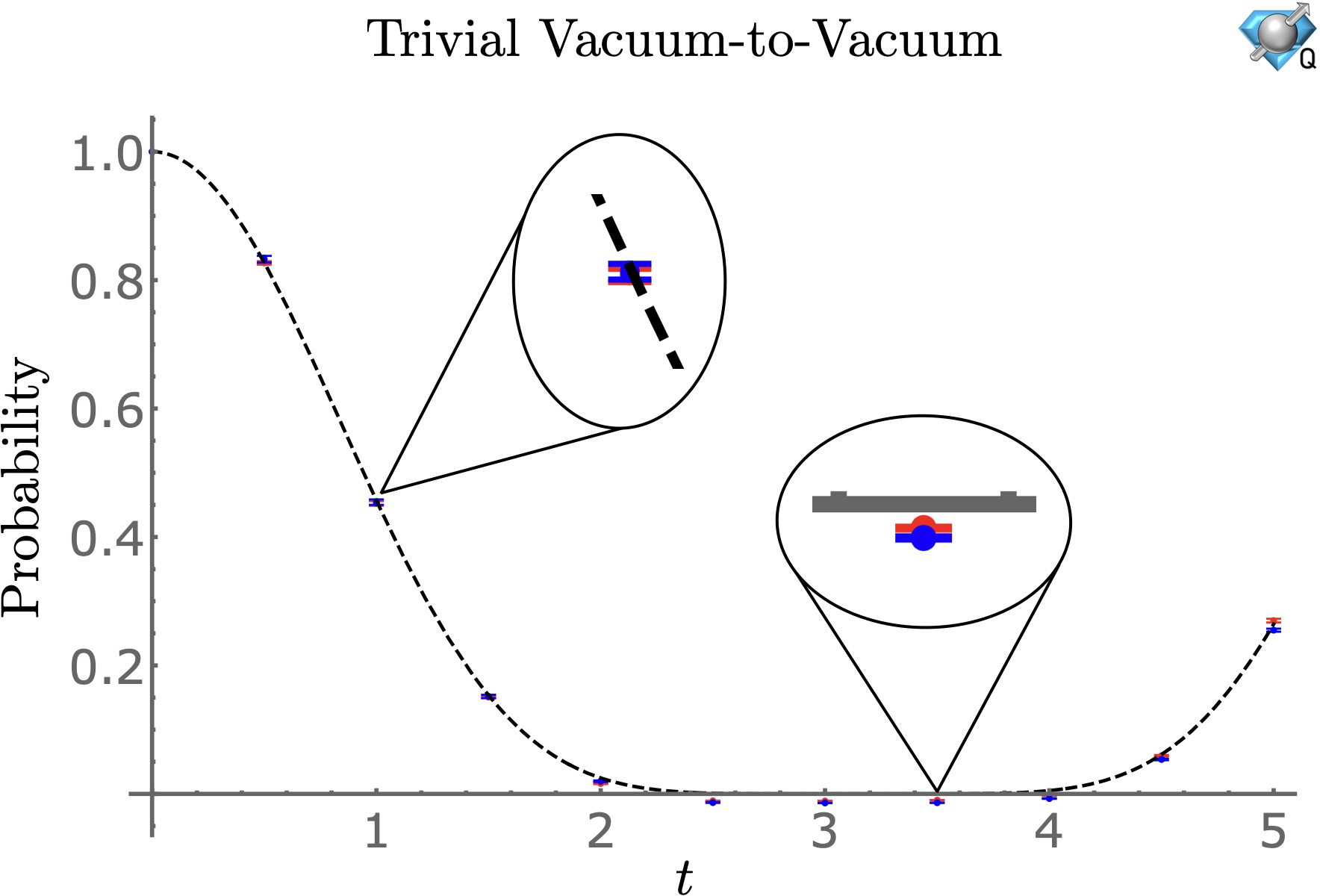
Preparations for Quantum Simulations of Quantum Chromodynamics in 1+1 Dimensions: (I) Axial Gauge
The resource requirements for quantum simulations of 1+1 dimensional quantum chromodynamics are estimated. When formulated in axial gauge and with two flavors of quarks, this system requires 12 qubits per spatial site once Gauss’s law has been enforced to uniquely constrain the gauge fields. Classical computations and D-Wave’s quantum annealer Advantage are used to determine the hadronic spectrum, enabling a decomposition of the masses and a study of quark entanglement. We identify color “edge” states, resulting from open boundary conditions, that are confined within a screening length to the end of the lattice. Quantum circuits for the time evolution of SU(Nc) gauge theory with Nf flavors of quarks are developed and used to determine the resources required for large-scale quantum simulations. IBM’s 7-qubit quantum computers ibmq_jakarta and ibm_perth were used to compute the trivial vacuum-to-vacuum and trivial vacuum-to-qr qr bar probabilities in Nf=1 QCD with one spatial site from one Trotter step of the time-evolution operator.
Quantum Monte Carlo in Configuration Space with Three-Nucleon Forces
Neutron matter, through its connection to neutron stars as well as systems like cold atom gases, is one of the most interesting yet accessible systems in nuclear physics. The Configuration-Interaction Monte Carlo (CIMC) method is a stochastic many-body technique allowing to tackle strongly coupled systems. In contrast to other Quantum Monte Carlo methods employed in nuclear physics, the CIMC method can be formulated directly in momentum space allowing for an efficient use of non-local interactions.
In this work we extend CIMC method to include three-nucleon interactions through the normal-ordered two-body approximation. We present results for the equation of state of neutron matter in line with other many-body calculations with low resolution chiral interactions, and provide predictions for the momentum distribution and the static structure factor.

Snowmass Computational Frontier: Topical Group Report on Quantum Computing
Quantum computing will play a pivotal role in the High Energy Physics (HEP) science program over the early parts of the Twenty First Century, both as a major expansion of our capabilities across the Computational Frontier, and in synthesis with quantum sensing and quantum networks. This report outlines how Quantum Information Science (QIS) and HEP are deeply intertwined endeavors that benefit enormously from a strong engagement together.
A number of problems ranging from simulation of quantum field theories, to fully leveraging the most sensitive sensor suites for new particle searches, and even data analysis will run into limiting bottlenecks if constrained to our current computing paradigms. Easy early access to quantum computers is needed to build a deeper understanding of these connections and the opportunities for advancement. In turn, HEP brings crucial expertise to the national quantum ecosystem in quantum domain knowledge, materials science, cryogenic and fast electronics, and massive-scale project management. The role of quantum technologies across the entire economy and society at large is expected to grow rapidly over the next decade, so it is important to establish the role of HEP in the efforts surrounding QIS. Fully delivering on the promise of quantum technologies and the goals of the HEP science program requires robust support. It is important to invest in the co-design opportunities afforded by the broader quantum computing ecosystem by leveraging HEP strengths in QIS for materials, electronics, and theory with the goal of designing quantum computers tailored to HEP science.
Quantum Simulation for High-energy Physics
It is for the first time that quantum simulation for high-energy physics (HEP) is studied in the U.S. decadal particle-physics community planning, and in fact until recently, this was not considered a mainstream topic in the community. This fact speaks of a remarkable rate of growth of this subfield over the past few years, stimulated by the impressive advancements in quantum-information sciences (QIS) and associated technologies over the past decade, and the significant investment in this area by the government and private sectors in the U.S. and other countries. High-energy physicists have quickly identified problems of importance to our understanding of nature at the most fundamental level, from tiniest distances to cosmological extents, that are intractable with classical computers but may benefit from quantum advantage. They have initiated, and continue to carry out, a vigorous program in theory, algorithm, and hardware co-design for simulations of relevance to the HEP mission. This community whitepaper is an attempt to bring this exciting and yet challenging area of research to the spotlight, and to elaborate on what the promises, requirements, challenges, and potential solutions are over the next decade and beyond.
This whitepaper is prepared for the topical groups CompF6 (Quantum computing), TF05 (Lattice Gauge Theory), and TF10 (Quantum Information Science) within the Computational Frontier and Theory Frontier of the U.S. Community Study on the Future of Particle Physics (Snowmass 2021).
From Asymptotic Freedom to Theta Vacua: Qubit Embeddings of the O(3) Nonlinear Sigma Model
Conventional lattice formulations of $\theta$ vacua in the $1+1$-dimensional $O(3)$ nonlinear sigma model suffer from a sign problem. Here, we construct the first sign-problem-free regularization for \emph{arbitrary} $\theta$. Using efficient lattice \ac{MC} computations, we demonstrate how a Hamiltonian model of spin-$\tfrac12$ degrees of freedom on a 2-dimensional spatial lattice reproduces both the infrared sector for arbitrary $\theta$, as well as the ultraviolet physics of asymptotic freedom. Furthermore, as a model of qubits on a two-dimensional square lattice with only nearest neighbor interactions, it is naturally suited for studying the physics of $\theta$ vacua and asymptotic freedom on near-term quantum devices. Our construction generalizes to $\theta$-vacua in all $\CP(N-1)$ models, solving a long standing sign problem.
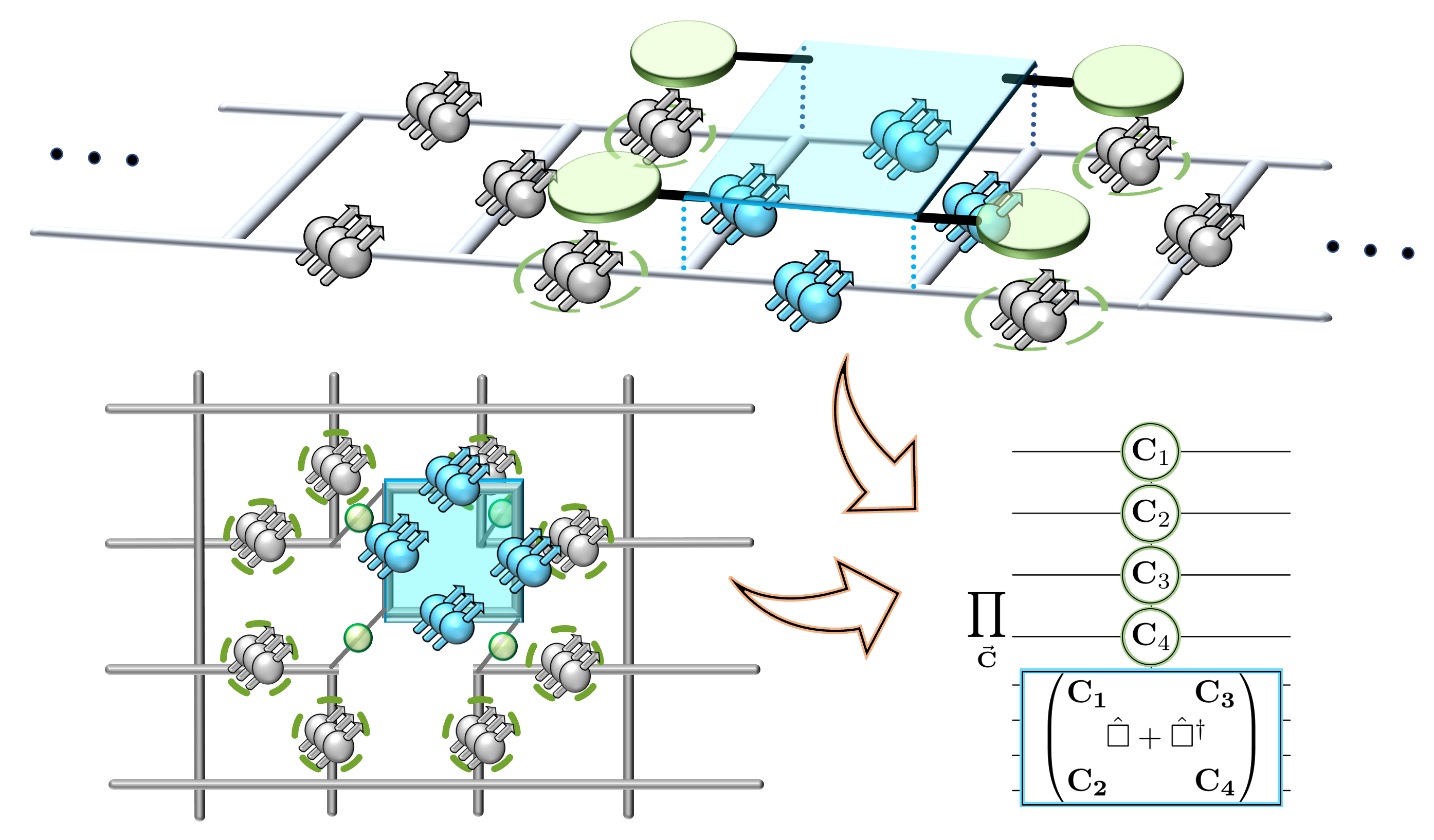
Some Conceptual Aspects of Operator Design for Quantum Simulations of Non-Abelian Lattice Gauge Theories
In the Kogut-Susskind formulation of lattice gauge theories, a set of quantum numbers resides at the ends of each link to characterize the vertex-local gauge field. We discuss the role of these quantum numbers in propagating correlations and generating entanglement that ensures each vertex remains gauge invariant, despite time evolution induced by operators with (only) partial access to each vertex Hilbert space. Applied to recent proposals for eliminating vertex-local Hilbert spaces in quantum simulation, we describe how the required entanglement is generated via delocalization of the time evolution operator with nearest-neighbor controls. These hybridizations, organized with qudits or qubits, exchange classical operator pre-processing for reductions in resource requirements that extend throughout the lattice volume.
(Contribution to proceedings of the 2021 Quantum Simulation for Strong Interactions (QuaSi) Workshops at the InQubator for Quantum Simulation (IQuS))
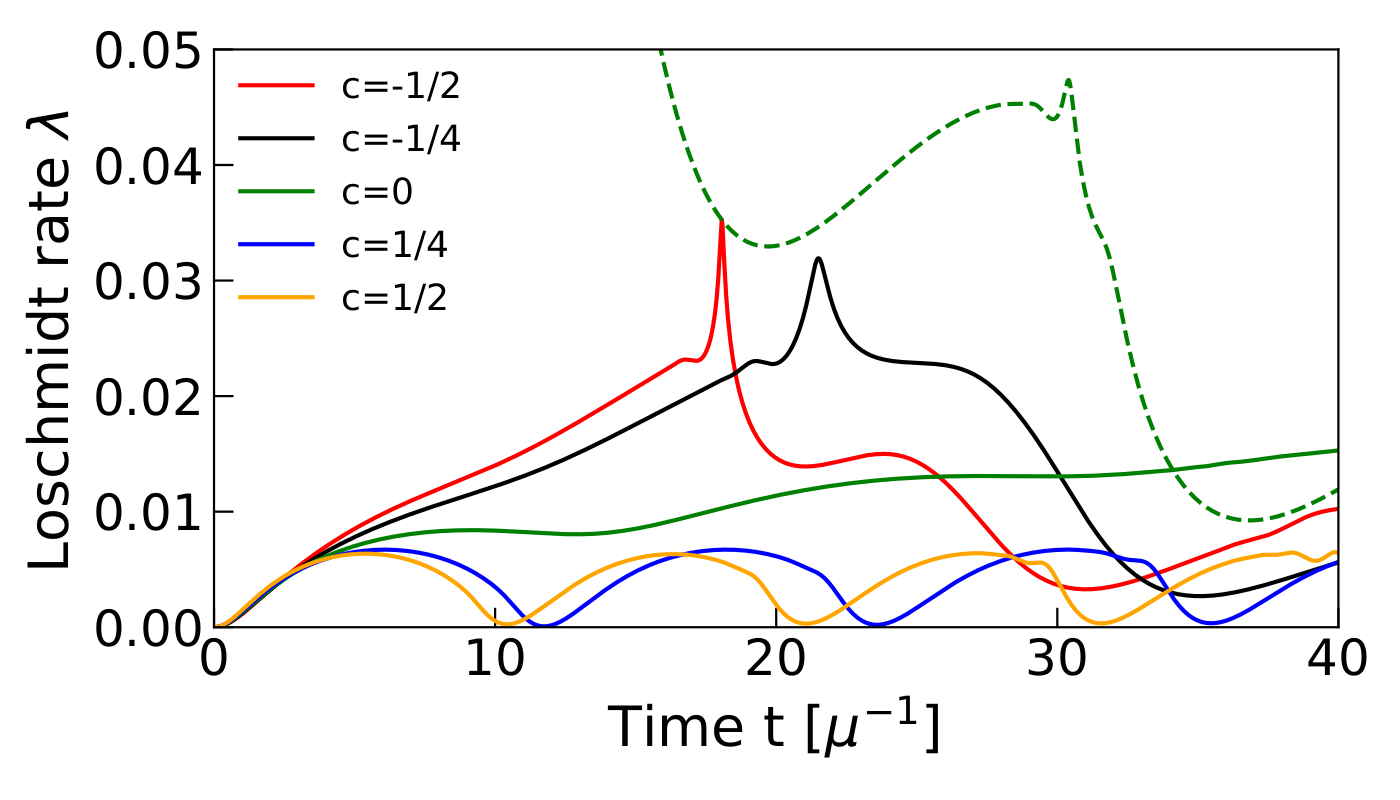
Entanglement and correlations in fast collective neutrino flavor oscillations
Collective neutrino oscillations play a crucial role in transporting lepton flavor in astrophysical settings like supernovae and neutron star binary merger remnants, which are characterized by large neutrino densities. In these settings, simulations in the mean-field approximation show that neutrino-neutrino interactions can overtake vacuum oscillations and give rise to fast collective flavor evolution on time-scales t ~ μ-1, with μ proportional to the local neutrino density. In this work, we study the full out-of-equilibrium flavor dynamics in simple multi-angle geometries displaying fast oscillations. Focusing on simple initial conditions, we analyze the production of pair correlations and entanglement in the complete many-body-dynamics as a function of the number N of neutrinos in the system.
Similarly to simpler geometries with only two neutrino beams, we identify three regimes: stable configurations with vanishing flavor oscillations, marginally unstable configurations with evolution occurring at long time scales τ~μ-1√N and unstable configurations showing flavor evolution on short time scales τ~μ-1log(N). We present evidence that these fast collective modes are generated by the same dynamical phase transition which leads to the slow bipolar oscillations, establishing a connection between these two phenomena and explaining the difference in their time scales.
We conclude by discussing a semi-classical approximation which reproduces the entanglement entropy at short to medium time scales and can be potentially useful in situations with more complicated geometries where classical simulation methods starts to become inefficient.
Large-charge conformal dimensions at the O(N) Wilson-Fisher fixed point
Recent work using a large-charge effective field theory (EFT) for the O(N) Wilson-Fisher conformal field theory has shown that the anomalous dimensions of large-charge operators can be expressed in terms of a few low-energy constants (LECs) of the EFT. By performing lattice Monte Carlo computations at the O(N) Wilson-Fisher critical point, we compute the anomalous dimensions of large-charge operators up to charge Q=10, and extract the leading and subleading LECs of the O(N) large-charge EFT for N=2,4,6,8. To alleviate the signal-to-noise ratio problem present in the large-charge sector of conventional lattice formulations of the O(N) theory, we employ a recently developed qubit formulation of the O(N) nonlinear sigma models with a worm algorithm. This enables us to test the validity of the large-charge expansion, and the recent predictions of large-N expansion for the coefficients of the large-charge EFT.
Qubit regularized O(N) nonlinear sigma models
Motivated by the prospect of quantum simulation of quantum field theories, we formulate the O(N) nonlinear sigma model as a “qubit” model with an (N+1)-dimensional local Hilbert space at each lattice site. Using an efficient worm algorithm in the worldline formulation, we demonstrate that the model has a second-order critical point in 2+1 dimensions, where the continuum physics of the nontrivial O(N) Wilson-Fisher fixed point is reproduced. We compute the critical exponents nu and eta for the O(N) qubit models up to N=8, and find excellent agreement with known results in literature from various analytic and numerical techniques for the O(N) Wilson-Fisher universality class. Our models are suited for studying O(N) nonlinear sigma models on quantum computers up to N=8 in d=2,3 spatial dimensions.
Basic Elements for Simulations of Standard Model Physics with Quantum Annealers: Multigrid and Clock States
We explore the potential of D-Wave’s quantum annealers for computing basic components required for quantum simulations of Standard Model physics. By implementing a basic multigrid (including zooming) and specializing Feynman-clock algorithms, D-Wave’s Advantage is used to study harmonic and anharmonic oscillators relevant for lattice scalar field theories and effective field theories, the time evolution of a single plaquette of SU(3) Yang-Mills lattice gauge field theory, and the dynamics of flavor entanglement in four neutrino systems.
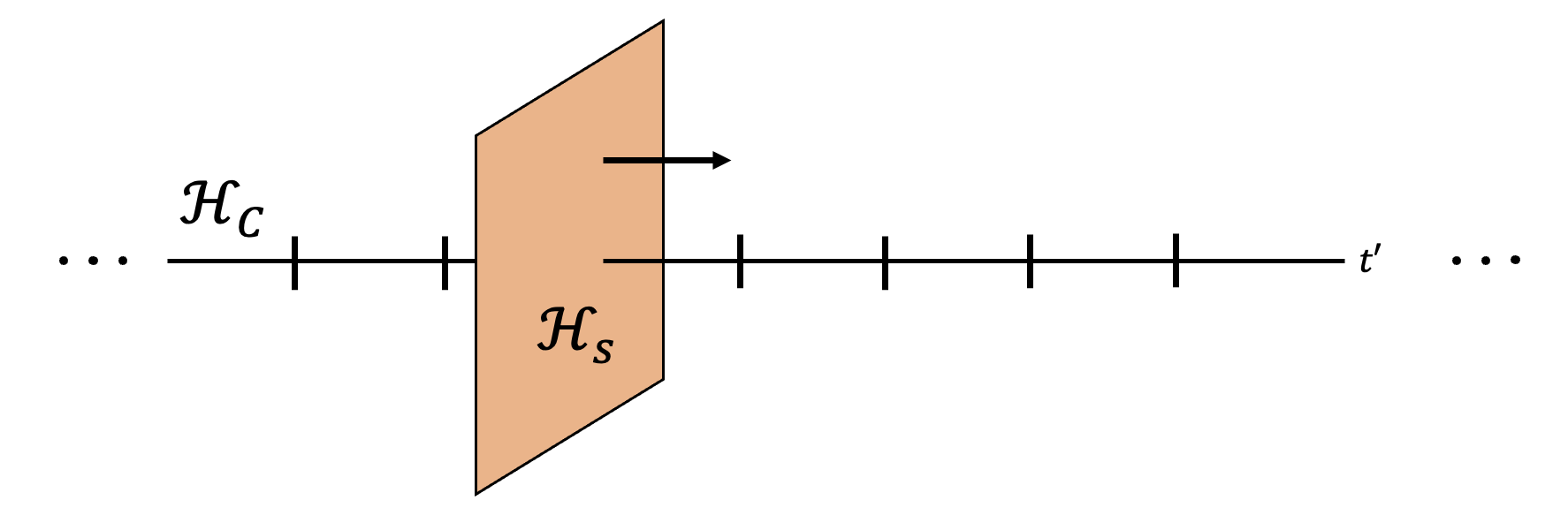
Time-dependent Hamiltonian Simulation Using Discrete Clock Constructions
In this work we provide a new approach for approximating an ordered operator exponential using
an ordinary operator exponential that acts on the Hilbert space of the simulation as well as a finite-
dimensional clock register. We show that as the number of qubits used for the clock grows, the error in
the ordered operator exponential vanishes, as well as the entanglement between the clock register and
the register of the state being acted upon. Hence, the clock is a convenient device that allows us to
translate results for simulating time-independent systems to the time-dependent case. As an application, we provide a new family of multiproduct formulas (MPFs) for time-dependent Hamiltonians that yield both commutator scaling and poly-logarithmic error scaling. This in turn, means that this method outperforms existing methods for simulating physically-local, time-dependent Hamiltonians. Finally, we apply the formalism to show how qubitization can be generalized to the time-dependent case and show that such a translation can be practical if the second derivative of the Hamiltonian is sufficiently small.

Nematic Confined Phases in the U(1) Quantum Link Model on a Triangular Lattice: An Opportunity for Near-Term Quantum Computations of String Dynamics on a Chip
The U(1) quantum link model on the triangular lattice has two rotation-symmetry-breaking nematic confined phases. Static external charges are connected by confining strings consisting of individual strands with fractionalized electric flux. The two phases are separated by a weak first order phase transition with an emergent almost exact SO(2) symmetry. We construct a quantum circuit on a chip to facilitate near-term quantum computations of the non-trivial string dynamics.
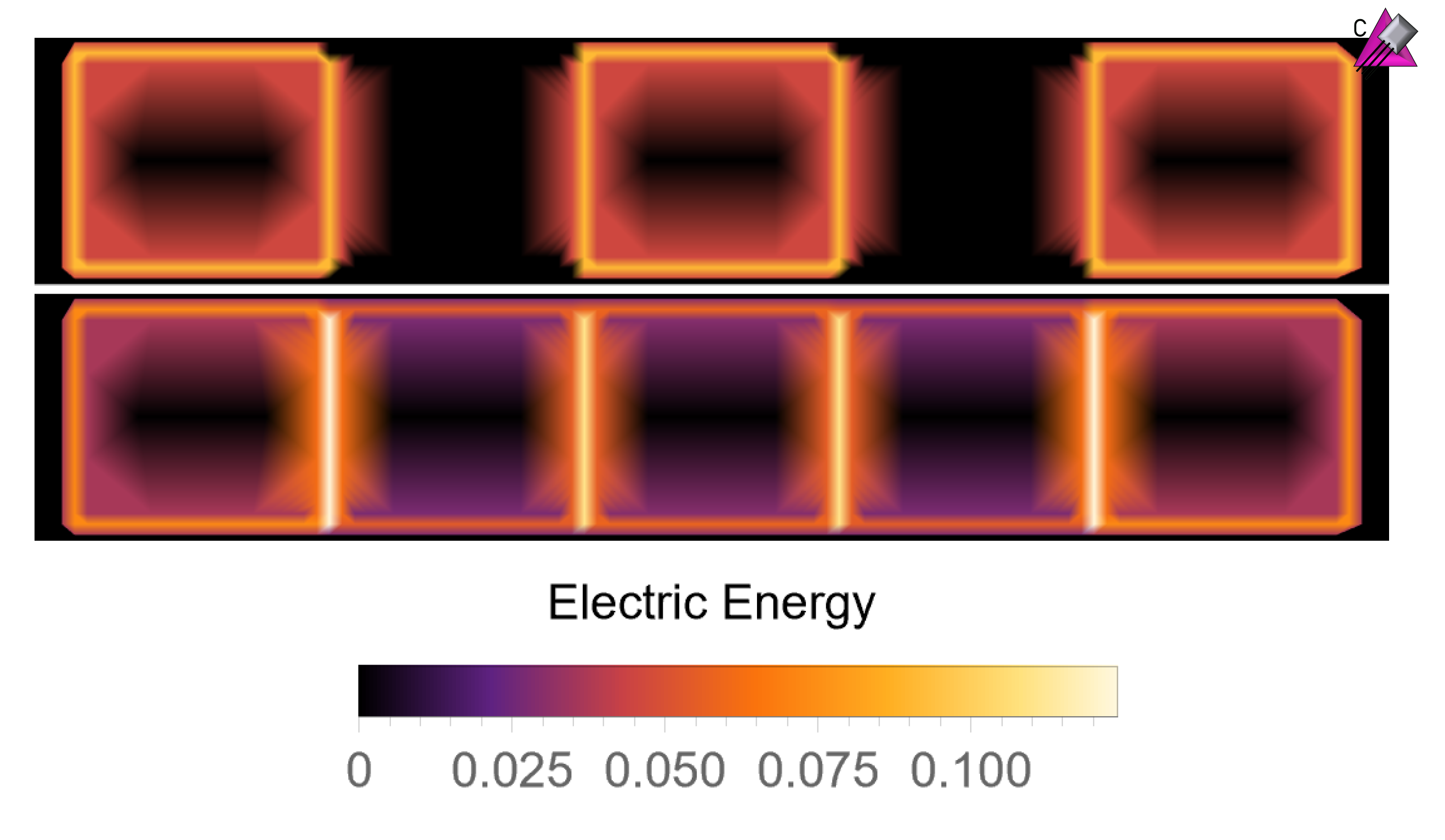
Preparation of the SU(3) Lattice Yang-Mills Vacuum with Variational Quantum Methods
Studying QCD and other gauge theories on quantum hardware requires the preparation of physically interesting states. The Variational Quantum Eigensolver (VQE) provides a way of performing vacuum state preparation on quantum hardware. In this work, VQE is applied to pure SU(3) lattice Yang-Mills on a single plaquette and one dimensional plaquette chains. Bayesian optimization and gradient descent were investigated for performing the classical optimization. Ansatz states for plaquette chains are constructed in a scalable manner from smaller systems using domain decomposition and a stitching procedure analogous to the Density Matrix Renormalization Group (DMRG). Small examples are performed on IBM’s superconducting Manila processor.
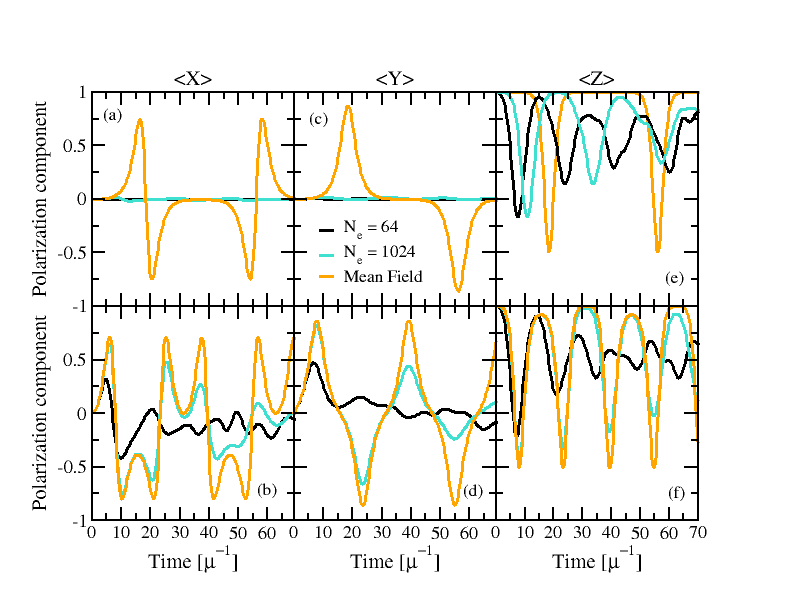
Classical and Quantum Evolution in a Simple Coherent Neutrino Problem
The extraordinary neutrino flux produced in extreme astrophysical environments like the early universe, core-collapse supernovae and neutron star mergers may produce coherent quantum neutrino oscillations on macroscopic length scales. The Hamiltonian describing this evolution can be mapped into quantum spin models with all-to-all couplings arising from neutrino-neutrino forward scattering. To date many studies of these oscillations have been performed in a mean-field limit where the neutrinos time evolve in a product state.
We examine a simple two-beam model evolving from an initial product state and compare the mean-field and many-body evolution. The symmetries in this model allow us to solve the real-time evolution for the quantum many-body system for hundreds or thousands of spins, far beyond what would be possible in a more general case with an exponential number (2N) of quantum states. We compare mean-field and many-body solutions for different initial product states and ratios of one- and two-body couplings, and find that in all cases in the limit of infinite spins the mean-field (product state) and many-body solutions coincide for simple observables. This agreement can be understood as a consequence of the spectrum of the Hamiltonian and the initial energy distribution of the product states. We explore quantum information measures like entanglement entropy and purity of the many-body solutions, finding intriguing relationships between the quantum information measures and the dynamical behavior of simple physical observables.
Causality and dimensionality in geometric scattering
The scattering matrix which describes low-energy,
non-relativistic scattering of two species of spin-1/2 fermions
interacting via finite-range potentials can be obtained from a
geometric action principle in which space and time do not appear
explicitly arXiv:2011.01278. In the case of zero-range
forces, constraints imposed by
causality –requiring that the scattered wave not be emitted before
the particles have interacted– translate into non-trivial
geometric constraints on scattering trajectories in the geometric
picture. The dependence of scattering on the number of spatial dimensions
is also considered; by varying from three to two spatial dimensions, the
dependence on spatial dimensionality in the geometric picture is
found to be encoded in the phase of the harmonic potential that appears in
the geometric action.
UV/IR symmetries of the S-matrix and RG flow
The low energy S-matrix which describes non-relativistic two-body
scattering arising from finite-range forces has UV/IR symmetries
that are hidden in the corresponding effective field theory (EFT) action.
It is shown that the S-matrix symmetries are manifest as geometric properties
of the RG flow of the coefficients of local operators in the EFT action.
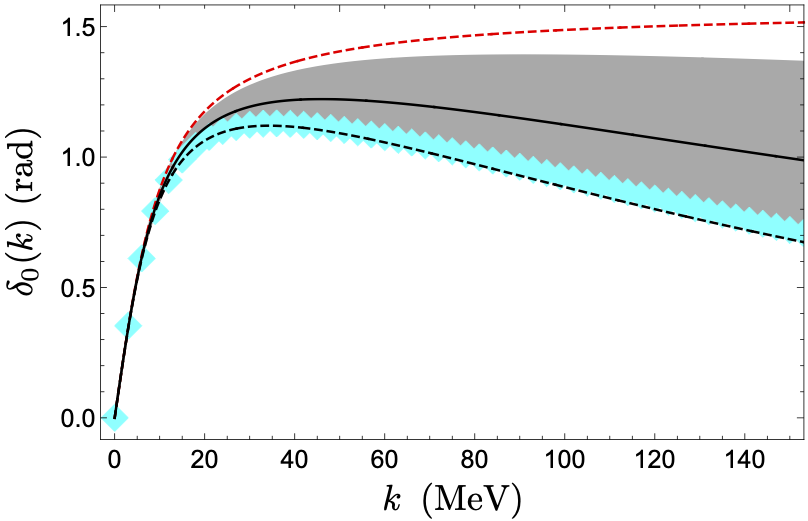
Symmetries of the nucleon-nucleon S-matrix and effective field theory expansions
The s-wave nucleon-nucleon (NN) scattering matrix
(S-matrix) exhibits UV/IR symmetries which are hidden in the
effective field theory (EFT) action and scattering amplitudes, and
which explain some interesting generic features of the phase
shifts. These symmetries offer clarifying interpretations of
existing pionless EFT expansions, and suggest starting points for
novel expansions. The leading-order (LO) S-matrix obtained in the
pionless EFT with scattering lengths treated exactly is shown to
have a UV/IR symmetry which leaves the sum of s-wave phase shifts
invariant. A new scheme, which treats effective range corrections
exactly, and which possesses a distinct UV/IR symmetry at LO, is
developed up to NLO (next-to-LO) and compared with data.
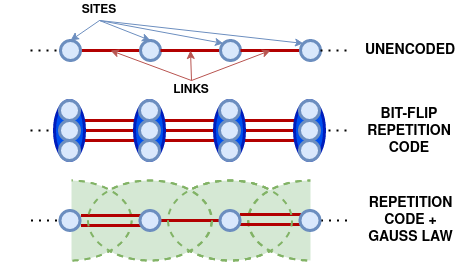
Quantum Error Correction with Gauge Symmetries
Quantum simulations of Lattice Gauge Theories (LGTs) are often formulated on an enlarged Hilbert space containing both physical and unphysical sectors in order to retain a local Hamiltonian. We provide simple fault-tolerant procedures that exploit such redundancy by combining a phase flip error correction code with the Gauss’ law constraint to correct one-qubit errors for a Z2 or truncated U(1) LGT in 1+1 dimensions with a link flux cutoff of 1. Unlike existing work on detecting violations of Gauss’ law, our circuits are fault tolerant and the overall error correction scheme outperforms a naive application of the [5,1,3] code. The constructions outlined can be extended to LGT systems with larger cutoffs and may be of use in understanding how to hybridize error correction and quantum simulation for LGTs in higher space-time dimensions and with different symmetry groups.
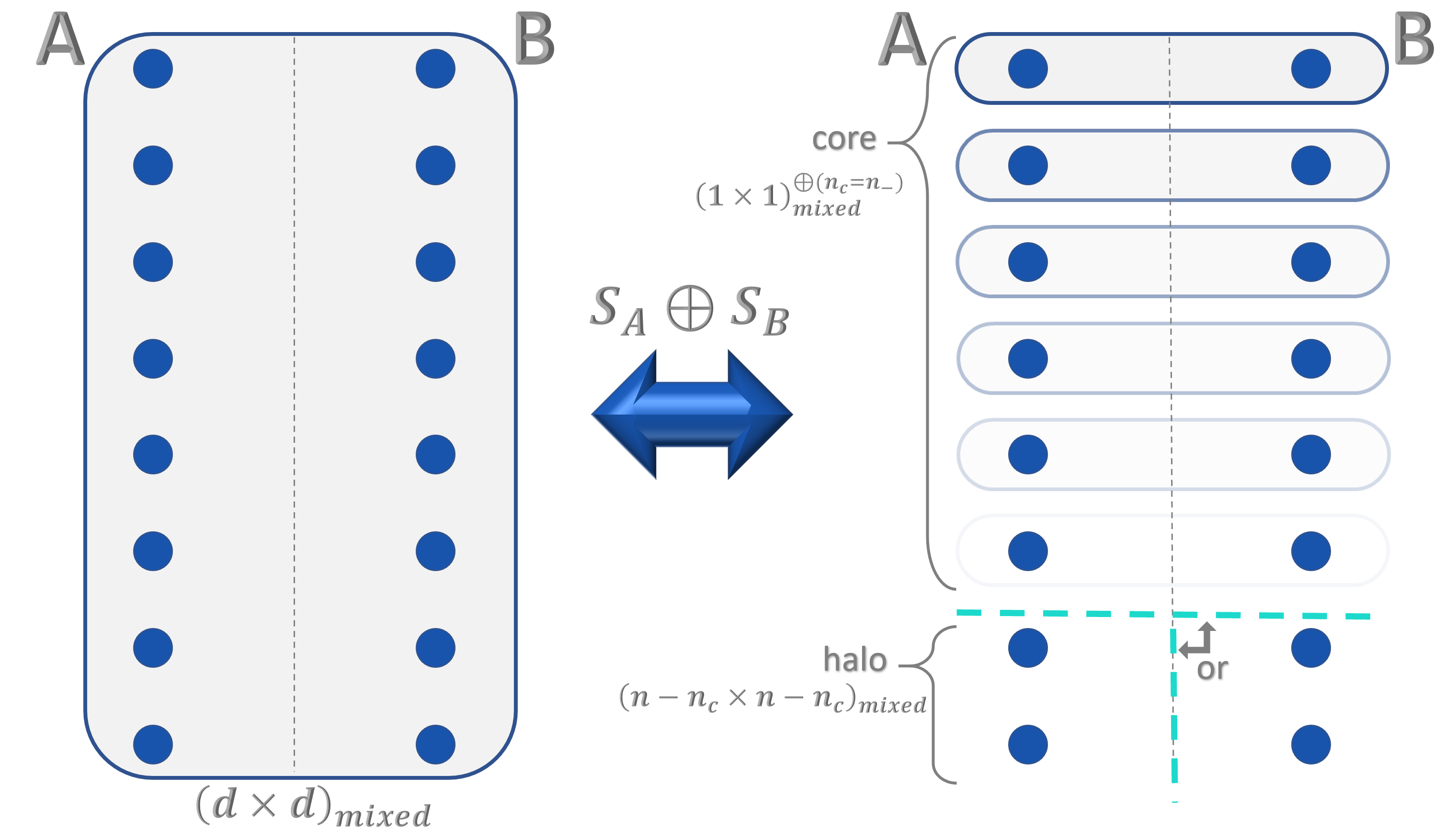
Entanglement Structures in Quantum Field Theories: Negativity Cores and Bound Entanglement in the Vacuum
The many-body entanglement between two finite (size-d) disjoint vacuum regions of noninteracting lattice scalar field theory in one spatial dimension, i.e., a (dA×dB)mixed Gaussian continuous variable system, is locally transformed into a tensor-product core of (1A×1B)mixed entangled pairs. Accessible entanglement within these core pairs exhibits an exponential hierarchy and as such identifies the structure of dominant region modes from which vacuum entanglement could be extracted into a spatially separated pair of quantum detectors. Beyond the core, the remaining modes of the halo are determined to be AB separable in isolation, as well as separable from the core. However, state preparation protocols that distribute entanglement in the form of (1A×1B)mixed core pairs are found to require additional entanglement in the halo that is obscured by classical correlations. This inaccessible (bound) halo entanglement is found to mirror the accessible entanglement, but with a step behavior as the continuum is approached. It remains possible that alternate initialization protocols that do not utilize the exponential hierarchy of core-pair entanglement may require less inaccessible entanglement. Entanglement consolidation is expected to persist in higher dimensions and may aid classical and quantum simulations of asymptotically free gauge field theories, such as quantum chromodynamics.
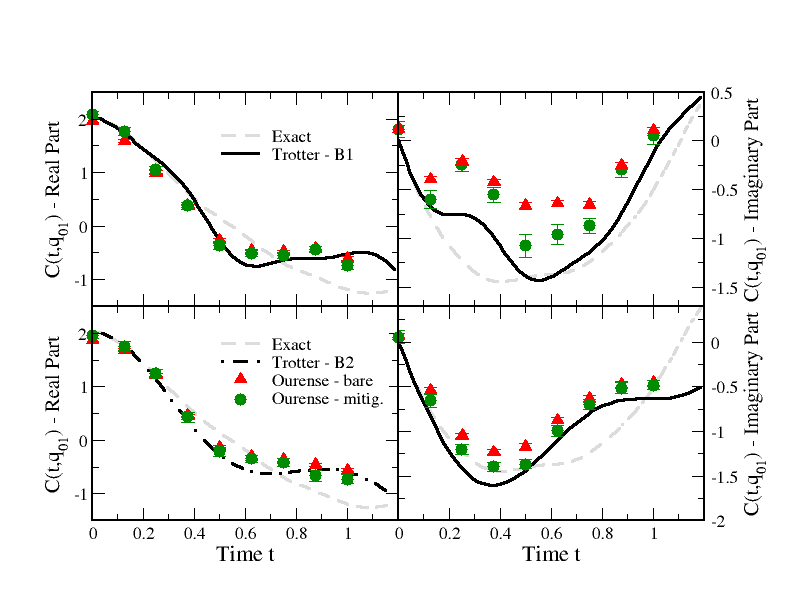
Nuclear two point correlation functions on a quantum computer
The calculation of dynamic response functions are expected to be an early application benefiting from rapidly developing quantum hardware resources. The ability to calculate real-time quantities of strongly-correlated quantum systems is one of the most exciting applications that can easily reach beyond the capabilities of traditional classical hardware. Response functions of fermionic systems at moderate momenta and energies corresponding roughly to the Fermi energy of the system are a potential early application because the relevant operators are nearly local and the energies can be resolved in moderately short real time, reducing the spatial resolution and gate depth required.
This is particularly the case in quasielastic electron and neutrino scattering from nuclei, a topic of great interest in the nuclear and particle physics communities and directly related to experiments designed to probe neutrino properties. In this work we use current hardware to calculate response functions for a highly simplified nuclear model through calculations of a 2-point real time correlation function for a Fermi-Hubbard model in two dimensions with three distinguishable nucleons on four lattice sites on current quantum hardware, and evaluate current error mitigation strategies.
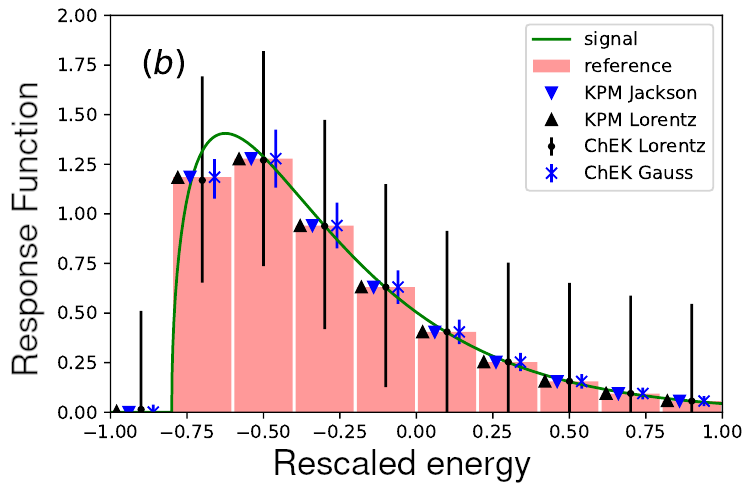
Spectral density reconstruction with Chebyshev polynomials
Accurate calculations of the spectral density in a strongly correlated quantum many body system are of fundamental importance to study many-particle dynamics in the linear response regime. Typical examples are the calculation of inclusive and semi-exclusive scattering cross sections in atomic nuclei and transport properties of nuclear and neutron star matter. Integral transform techniques have played an important role in accessing the spectral density in a variety of nuclear systems. However, their accuracy is in practice limited by the need to perform a numerical inversion which is often ill-conditioned.
In order to circumvent this problem, a quantum algorithm based on an appropriate expansion in Chebyshev polynomials was recently proposed. In the present work we build on this idea. We show how to perform controllable reconstructions of the spectral density over a finite energy resolution with rigorous error estimates while allowing for efficient simulations on classical computers. We apply our idea to simple model response functions and comment on the applicability of the method to study realistic systems using scalable nuclear many-body methods.
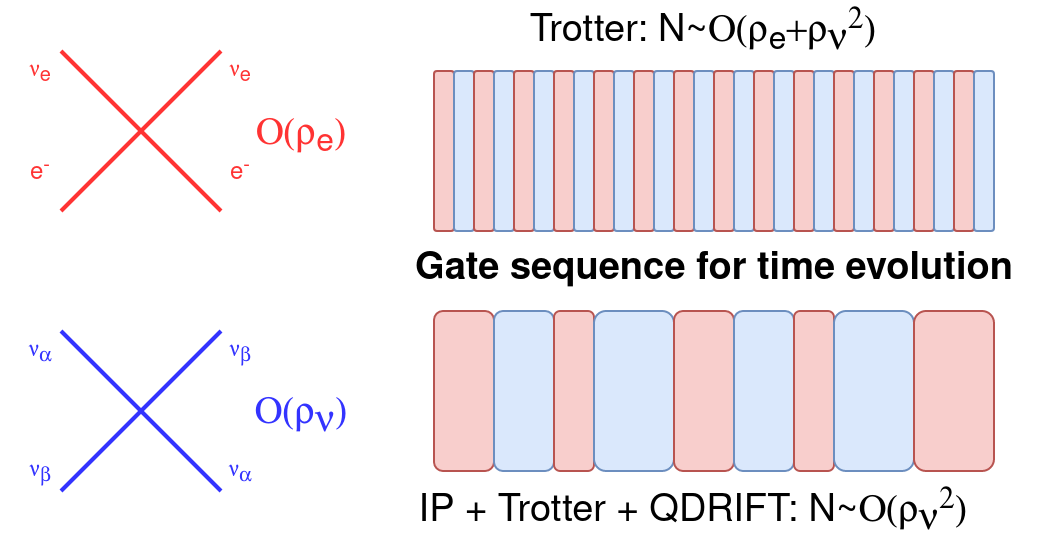
Hybridized Methods for Quantum Simulation in the Interaction Picture
Conventional methods of quantum simulation involve trade-offs that limit their applicability to specific contexts where their use is optimal. This paper demonstrates how different simulation methods can be hybridized to improve performance for interaction picture simulations over known algorithms. These approaches show asymptotic improvements over the individual methods that comprise them and further make interaction picture simulation methods practical in the near term. Physical applications of these hybridized methods yields a gate complexity scaling as log²Λ in the electric cutoff Λ for the Schwinger Model and independent of the electron density for collective neutrino oscillations, outperforming the scaling for all current algorithms with these parameters. For the general problem of Hamiltonian simulation subject to dynamical constraints, these methods yield a query complexity independent of the penalty parameter λ used to impose an energy cost on time-evolution into an unphysical subspace.
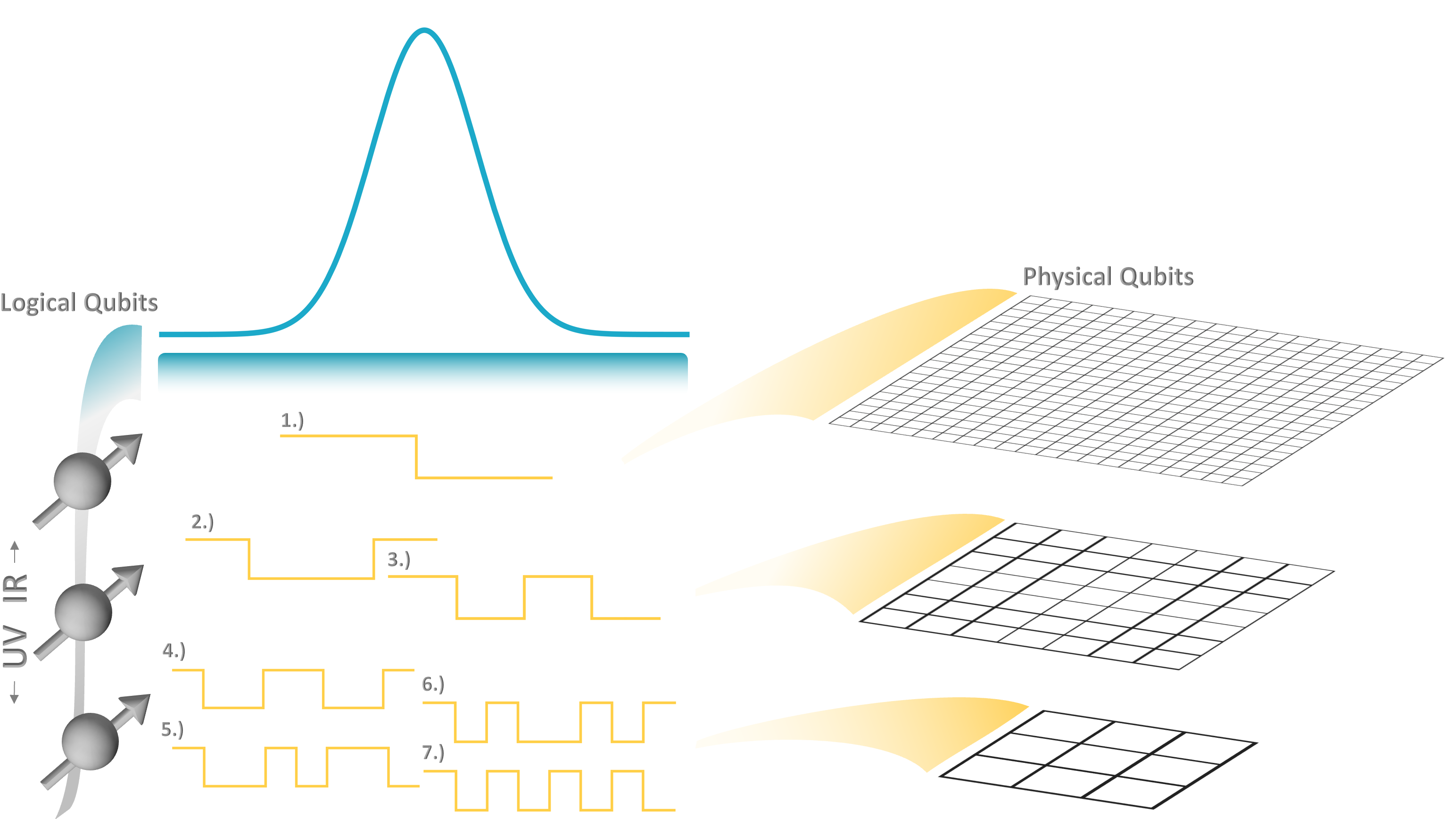
Hierarchical Qubit Maps and Hierarchical Quantum Error Correction
We consider hierarchically implemented quantum error correction (HI-QEC) in which the fidelities of logical qubits are differentially optimized to enhance the capabilities of quantum devices in scientific applications. By employing qubit representations that propagate hierarchies in simulated systems to those in logical qubit noise sensitivities, heterogeneity in the distribution of physical qubits among logical qubits can be systematically structured. For concreteness, we estimate HI-QEC’s impact on surface code resources in computing low-energy observables to a fixed precision, finding up to ~60% reductions in qubit requirements possible in early error corrected simulations. This heterogeneous distribution of physical-to-logical qubits is identified as another element that can be optimized in the co-design process of quantum simulations of Standard Model physics.
Entanglement minimization in hadronic scattering with pions
Recent work conjectured that
entanglement is minimized in low-energy hadronic scattering
processes. It was shown that the minimization of the entanglement
power (EP) of the low-energy baryon-baryon S-matrix implies novel
spin-flavor symmetries that are distinct from large-N_c QCD
predictions and are confirmed by high-precision lattice QCD
simulations. Here the conjecture of minimal entanglement is
investigated for scattering processes involving pions and
nucleons. The EP of the S-matrix is constructed for the pi-pi
and pi-N systems, and the consequences of minimization of
entanglement are discussed and compared with large-N_c QCD
expectations.
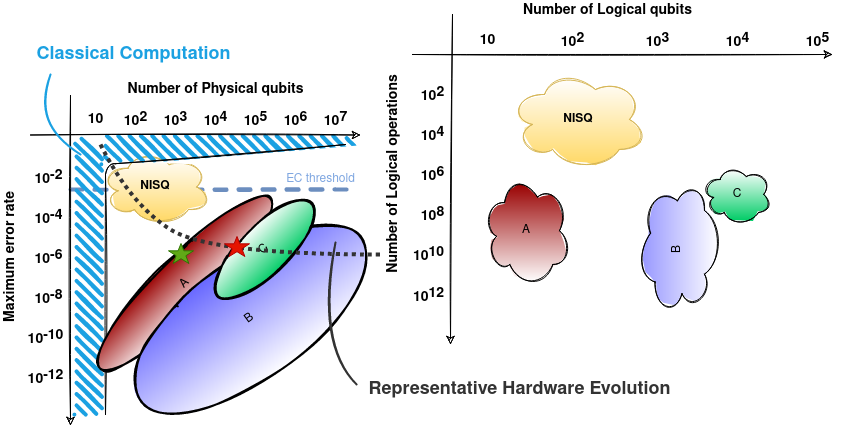
Standard Model Physics and the Digital Quantum Revolution: Thoughts about the Interface
Remarkable advances in isolating, controlling and entangling quantum systems are transforming what was once a curious feature of quantum mechanics into a vehicle for disruptive scientific and technological progress. Pursuing the vision articulated by Feynman, a concerted effort across many areas of research and development is introducing prototypical digital quantum devices into the computing ecosystem available to domain scientists. Through interactions with these early quantum devices, the abstract vision of exploring classically-intractable quantum systems is evolving toward becoming a tangible reality. Beyond catalyzing these technological advances, entanglement is enabling parallel progress as a diagnostic for quantum correlations and as an organizational tool, both guiding improved understanding of quantum many-body systems and quantum field theories defining and emerging from the Standard Model. From the perspective of three domain science theorists, this article compiles “thoughts about the interface” on entanglement, complexity, and quantum simulation in an effort to contextualize recent NISQ-era progress with the scientific objectives of nuclear and high-energy physics.
Quantum Machine Learning with SQUID
In this work we present the Scaled QUantum IDentifier (SQUID), an open-source framework for exploring hybrid Quantum-Classical algorithms for classification problems. The classical infrastructure is based on PyTorch and we provide a standardized design to implement a variety of quantum models with the capability of back-propagation for efficient training. We present the structure of our framework and provide examples of using SQUID in a standard binary classification problem from the popular MNIST dataset. In particular we highlight the implications for scalability for gradient based optimization of quantum models on the choice of output for variational quantum models.
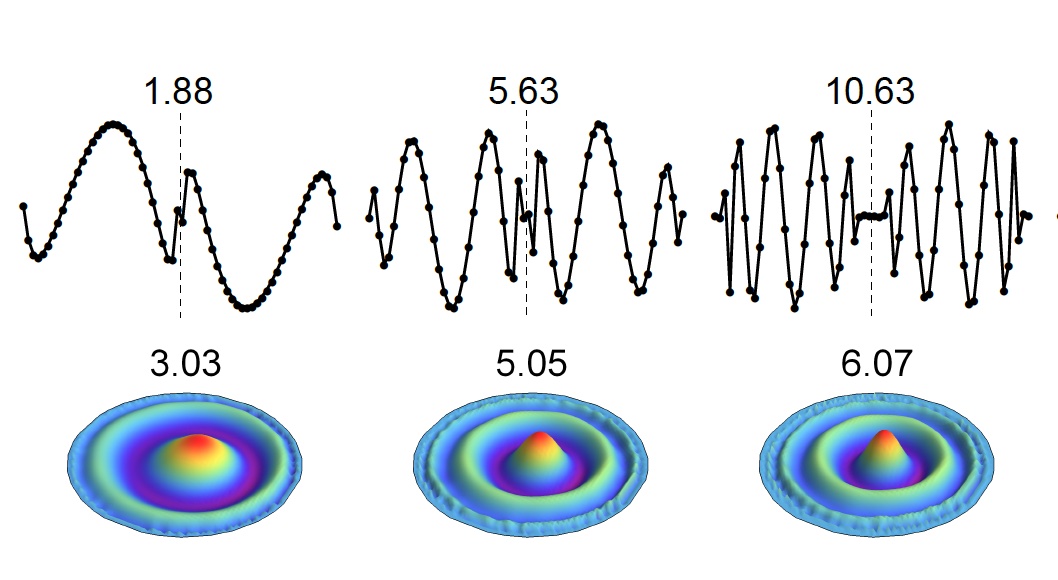
Entanglement Spheres and a UV-IR connection in Effective Field Theories
Disjoint regions of the latticized, massless scalar field vacuum become separable at large distances beyond the entanglement sphere, a distance that extends to infinity in the continuum limit. Through numerical calculations in one-, two- and three-dimensions, the radius of an entanglement sphere is found to be determined by the highest momentum mode of the field supported across the diameter, d, of two identical regions. As a result, the long-distance behavior of the entanglement is determined by the short-distance structure of the field. Effective eld theories (EFTs), describing a system up to a given momentum scale Lambda, are expected to share this feature, with regions of the EFT vacuum separable (or dependent on the UV-completion) beyond a distance proportional to Λ. The smallest non-zero value of the entanglement negativity supported by the field at large distances is conjectured to be NN~exp(-Λ d), independent of the number of spatial dimensions. This phenomenon may be manifest in perturbative QCD processes.
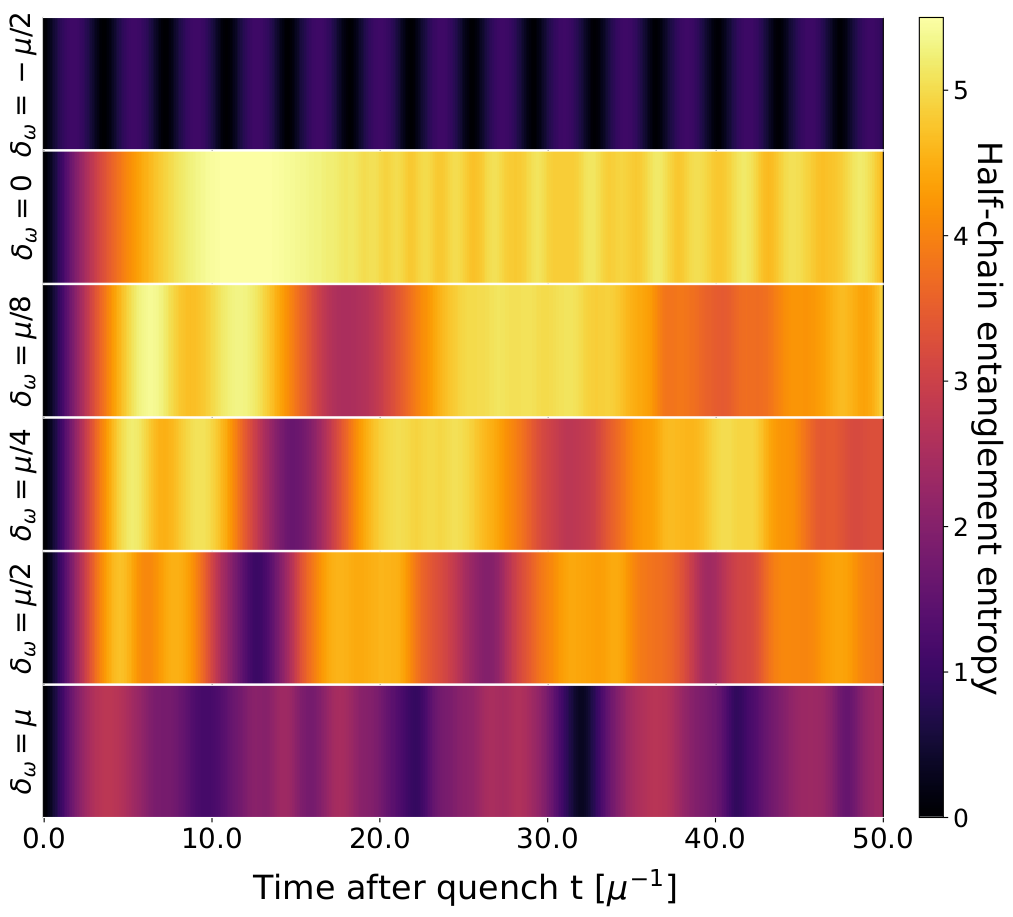
Dynamical Phase Transitions in models of Collective Neutrino Oscillations
Collective neutrino oscillations can potentially play an important role in transporting lepton flavor in astrophysical scenarios where the neutrino density is large, typical examples are the early universe and supernova explosions. It has been argued in the past that simple models of the neutrino Hamiltonian designed to describe forward scattering can support substantial flavor evolution on very short time scales t≈log(N)/(GFρ), with N the number of neutrinos, GF the Fermi constant and ρ the neutrino density. This finding is in tension with results for a similar but exactly solvable model for which t≈√N/(GFρ) instead. In this work we provide a coherent explanation of this tension in terms of Dynamical Phase Transitions (DPT) and study the possible impact that a DPT could have in more realistic models of neutrino oscillations and their mean-field approximation.
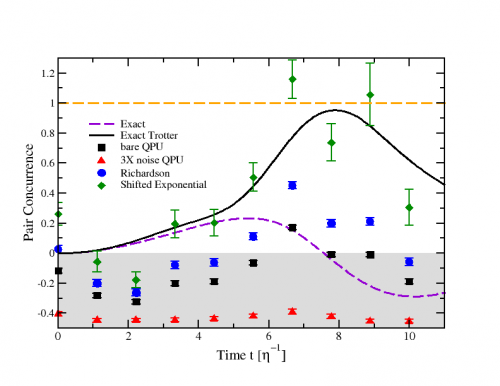
Simulation of Collective Neutrino Oscillations on a Quantum Computer
In astrophysical scenarios with large neutrino density, like supernovae and the early universe, the presence of neutrino-neutrino interactions can give rise to collective flavor oscillations in the out-of-equilibrium collective dynamics of a neutrino cloud. The role of quantum correlations in these phenomena is not yet well understood, in large part due to complications in solving for the real-time evolution of the strongly coupled many-body system. Future fault-tolerant quantum computers hold the promise to overcome much of these limitations and provide direct access to the correlated neutrino dynamic. In this work, we present the first simulation of a small system of interacting neutrinos using current generation quantum devices. We introduce a strategy to overcome limitations in the natural connectivity of the qubits and use it to track the evolution of entanglement in real-time. The results show the critical importance of error-mitigation techniques to extract meaningful results for entanglement measures using noisy, near term, quantum devices.
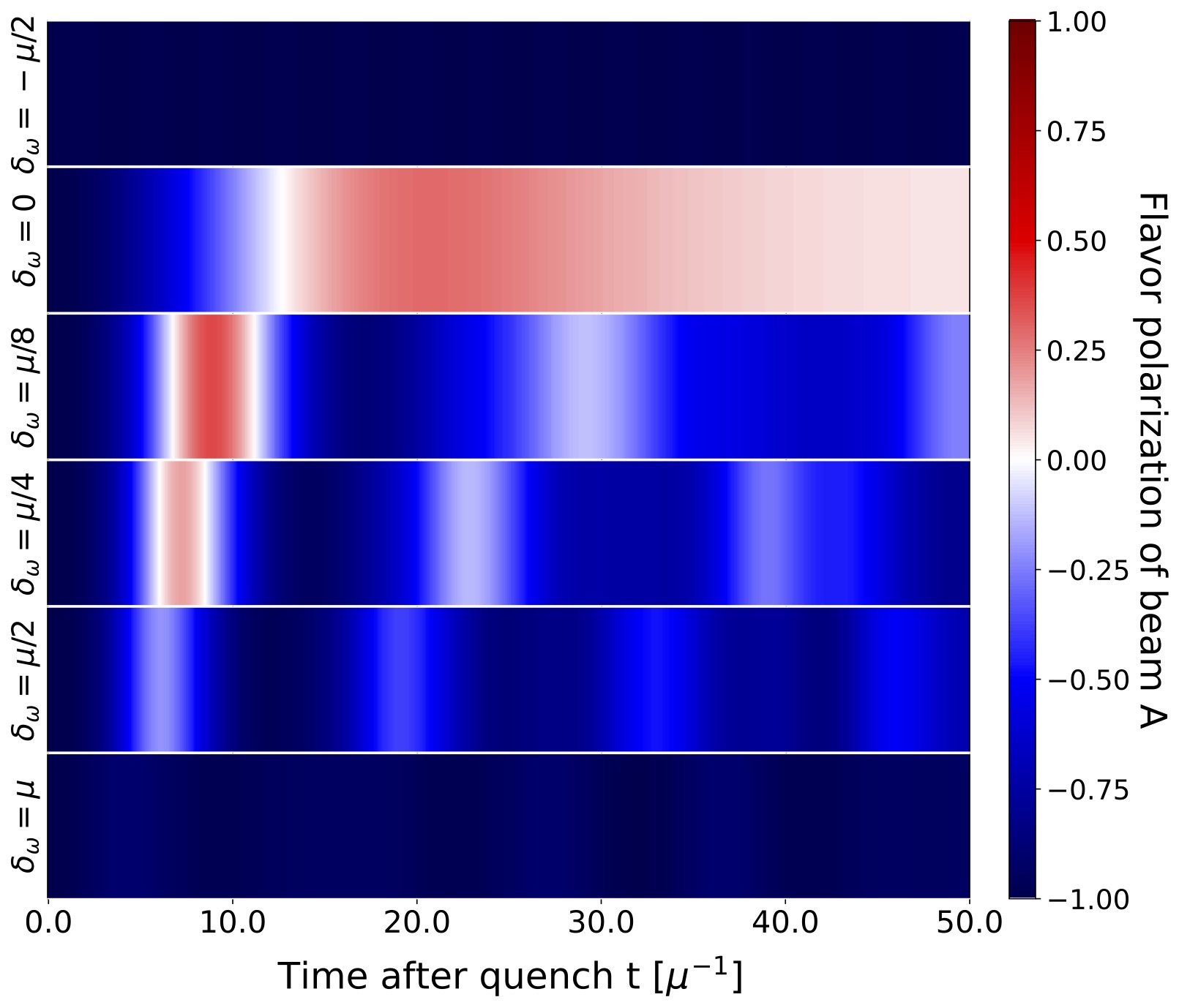
Entanglement and Many-Body Effects in Collective Neutrino Oscillations
Collective neutrino oscillations play a crucial role in transporting lepton flavor in astrophysical settings, such as supernovae, where the neutrino density is large. In this regime, neutrino-neutrino interactions are important and simulations in mean-field approximations show evidence for collective oscillations occurring at time scales much larger than those associated with vacuum oscillations. In this work, we study the out-of-equilibrium dynamics of a corresponding spin model using Matrix Product States and show how collective bipolar oscillations can be triggered by quantum fluctuations if appropriate initial conditions are present. The origin of these flavor oscillations, absent in the mean-field, can be traced to the presence of a dynamical phase transition, which drastically modifies the real-time evolution of the entanglement entropy. We find entanglement entropies scaling at most logarithmically in the system size, suggesting that classical tensor network methods could be efficient in describing collective neutrino dynamics more generally.
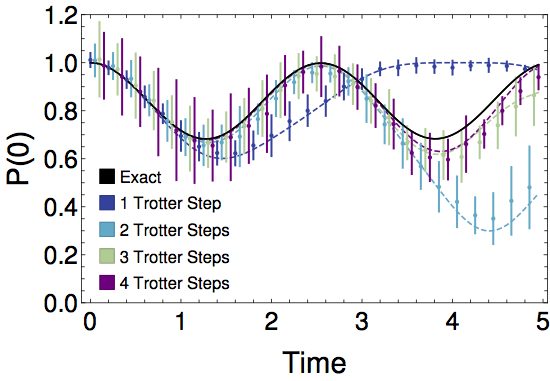
A Trailhead for Quantum Simulation of SU(3) Yang-Mills Lattice Gauge Theory in the Local Multiplet Basis
Maintaining local interactions in the quantum simulation of gauge field theories relegates most states in the Hilbert space to be unphysical—theoretically benign, but experimentally difficult to avoid. Reformulations of the gauge fields can modify the ratio of physical to gauge-variant states often through classically preprocessing the Hilbert space and modifying the representation of the field on qubit degrees of freedom. This paper considers the implications of representing SU(3) Yang-Mills gauge theory on a lattice of irreducible representations in both a global basis of projected global quantum numbers and a local basis in which controlled-plaquette operators support efficient time evolution. Classically integrating over the internal gauge space at each vertex (e.g., color isospin and color hypercharge) significantly reduces both the qubit requirements and the dimensionality of the unphysical Hilbert space. Initiating tuning procedures that may inform future calculations at scale, the time evolution of one- and two-plaquettes are implemented on one of IBM’s superconducting quantum devices, and early benchmark quantities are identified. The potential advantages of qudit environments, with either constrained 2D hexagonal or 1D nearest-neighbor internal state connectivity, are discussed for future large-scale calculations.
Editors Suggestion in Physical Review D.
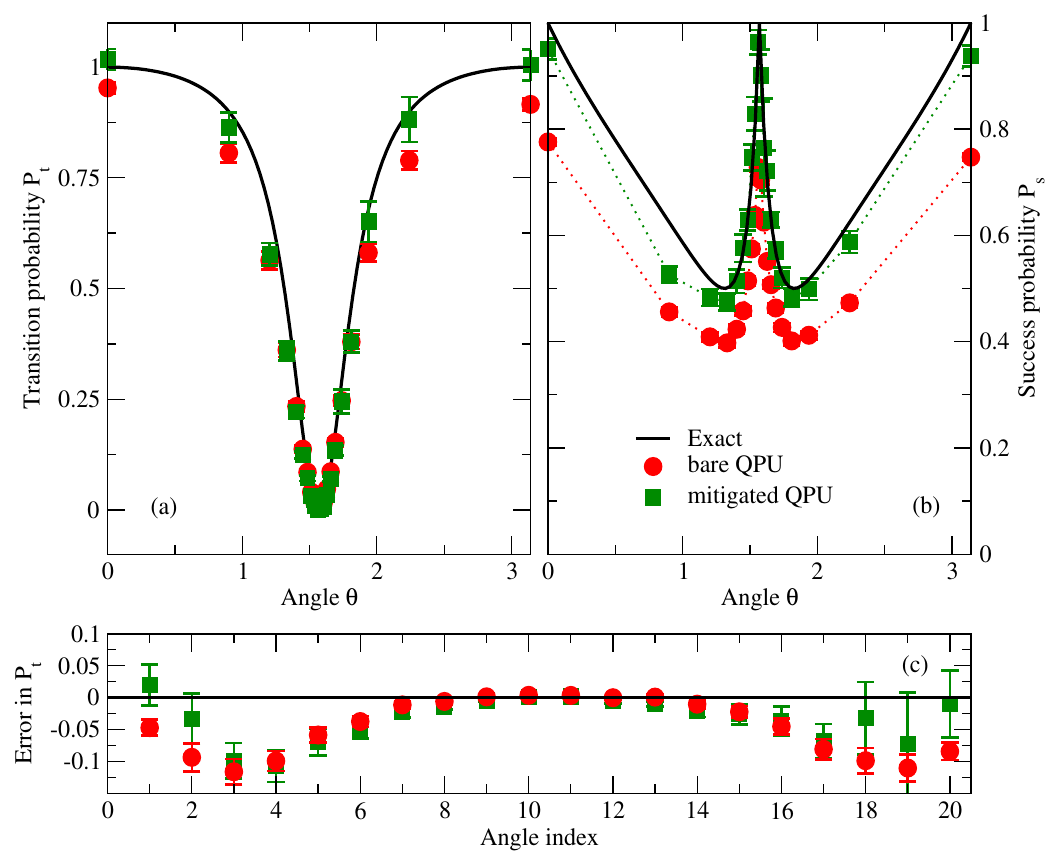
Preparation of Excited States for Nuclear Dynamics on a Quantum Computer
We study two different methods to prepare excited states on a quantum computer, a key initial step to study dynamics within linear response theory. The first method uses unitary evolution for a short timeT=O(√(1−F)) to approximate the action of an excitation operator O with fidelity Fand success probability P≈1−F. The second method probabilistically applies the excitation operator using the Linear Combination of Unitaries (LCU) algorithm. We benchmark these techniques on emulated and real quantum devices, using a toy model for thermal neutron-proton capture. Despite its larger memory footprint, the LCU-based method is efficient even on current generation noisy devices and can be implemented at a lower gate cost than a naive analysis would suggest. These findings show that quantum techniques designed to achieve good asymptotic scaling on fault tolerant quantum devices might also provide practical benefits on devices with limited connectivity and gate fidelity.
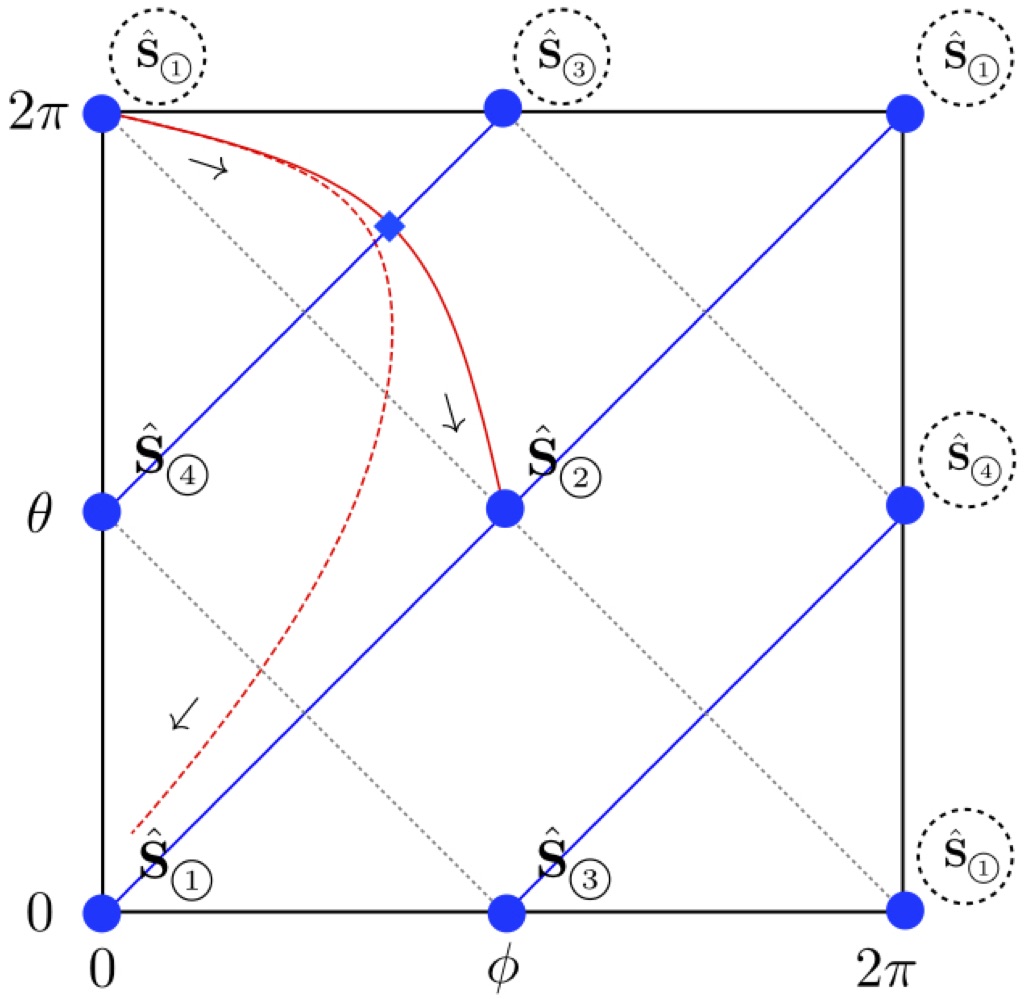
Geometry and entanglement in the scattering matrix
A formulation of nucleon-nucleon scattering is developed in which the S-matrix, rather than an effective-field theory (EFT) action, is the fundamental object. Spacetime plays no role in this description: the S-matrix is a trajectory that moves between RG fixed points in a compact theory space defined by unitarity. This theory space has a natural operator definition, and a geometric embedding of the unitarity constraints in four-dimensional Euclidean space yields a flat torus, which serves as the stage on which the S-matrix propagates. Trajectories with vanishing entanglement are special geodesics between RG fixed points on the flat torus, while entanglement is driven by an external potential. The system of equations describing S-matrix trajectories is in general complicated, however the very-low-energy S-matrix — that appears at leading-order in the EFT description — possesses a UV/IR conformal invariance which renders the system of equations integrable, and completely determines the potential. In this geometric viewpoint, inelasticity is in correspondence with the radius of a three-dimensional hyperbolic space whose two-dimensional boundary is the flat torus. This space has a singularity at vanishing radius, corresponding to maximal violation of unitarity. The trajectory on the flat torus boundary can be explicitly constructed from a bulk trajectory with a quantifiable error, providing a simple example of a holographic quantum error correcting code.
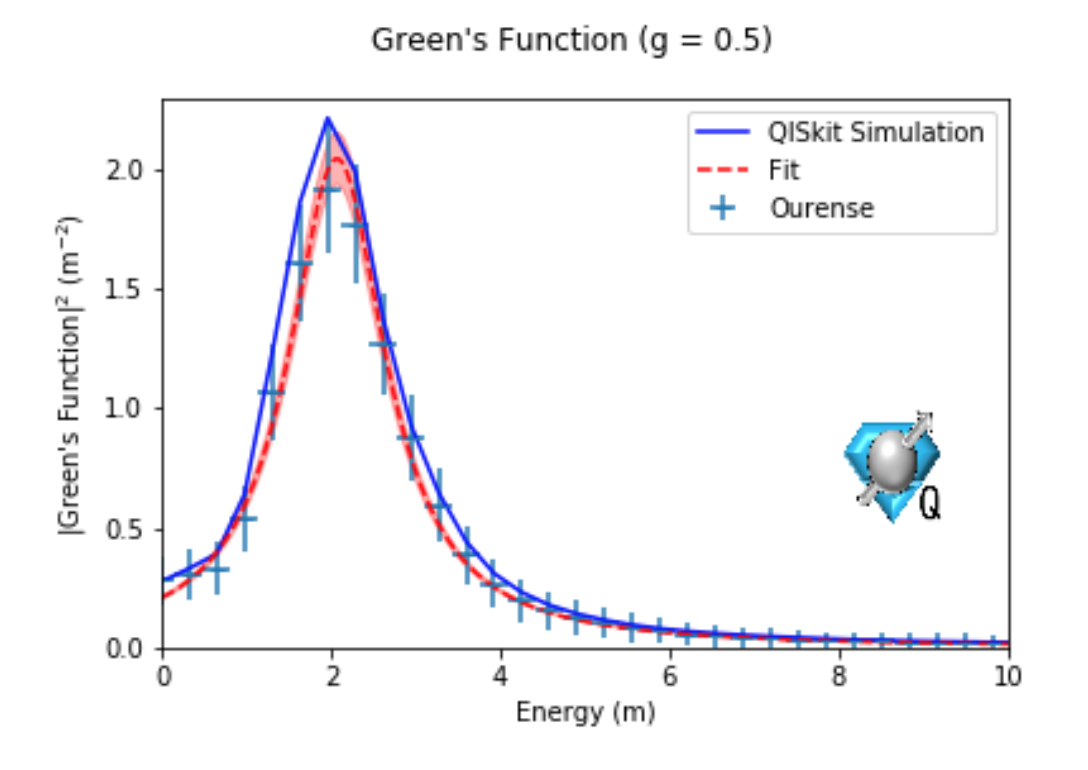
An Algorithm for Quantum Computation of Particle Decays
A quantum algorithm is developed to calculate decay rates and cross sections using quantum resources that scale polynomially in the system size assuming similar scaling for state preparation and time evolution. This is done by computing finite-volume one- and two-particle Green’s functions on the quantum hardware. Particle decay rates and two particle scattering cross sections are extracted from the imaginary parts of the Green’s function. A 0 + 1 dimensional implementation of this method is demonstrated on IBM’s superconducting quantum hardware for the decay of a heavy scalar particle to a pair of light scalars.
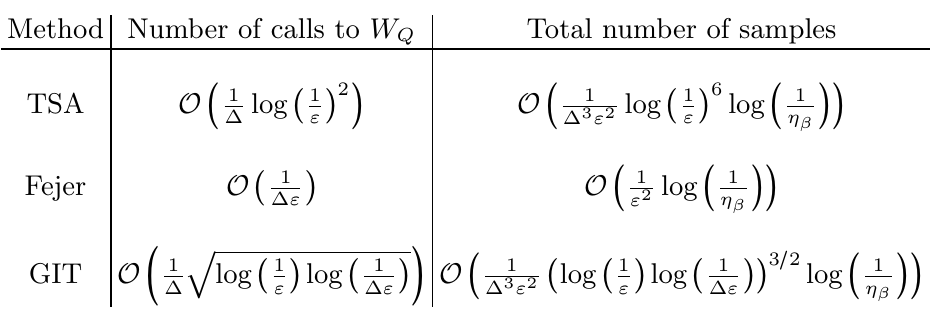
Spectral Density Estimation with the Gaussian Integral Transform
The spectral density operator ρ(ω)=δ(ω−H) plays a central role in linear response theory as it’s expectation value, the dynamical response function, can be used to compute scattering cross-sections. In this work, we describe a near optimal quantum algorithm providing an approximation to the spectral density with energy resolution Δ and error ϵ using O(√(log(1/ϵ)(log(1/Δ)+log(1/ϵ)))/Δ) operations. This is achieved without using expensive approximations to the time-evolution operator but exploiting instead qubitization to implement an approximate Gaussian Integral Transform (GIT) of the spectral density. We also describe appropriate error metrics to assess the quality of spectral function approximations more generally.

Geometric Quantum Information Structure in Quantum Fields and their Lattice Simulation
An upper limit to distillable entanglement between two disconnected regions of massless noninteracting scalar field theory has an exponential decay defined by a geometric decay constant. When regulated at short distances with a spatial lattice, this entanglement abruptly vanishes beyond a dimensionless separation, defining a negativity sphere. In two spatial dimensions, we determine this geometric decay constant between a pair of disks and the growth of the negativity sphere toward the continuum through a series of lattice calculations. Making the connection to quantum field theories in three-spatial dimensions, assuming such quantum information scales appear also in quantum chromodynamics (QCD), a new relative scale may be present in effective field theories describing the low-energy dynamics of nucleons and nuclei. We highlight potential impacts of the distillable entanglement structure on effective field theories, lattice QCD calculations and future quantum simulations.
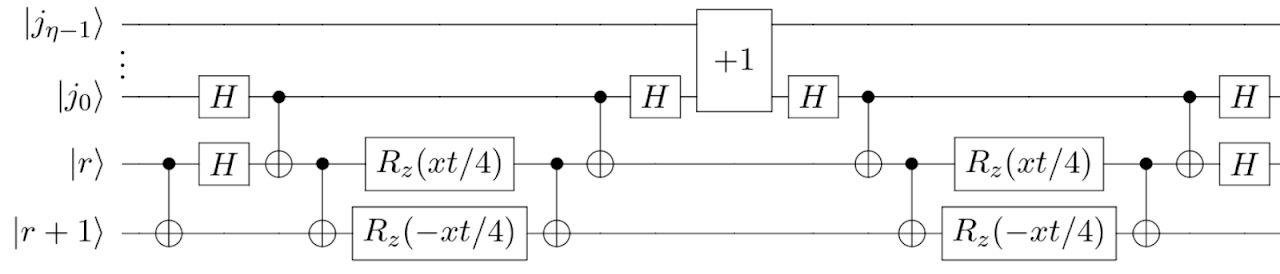
Quantum Algorithms for Simulating the Lattice Schwinger Model
The Schwinger model (quantum electrodynamics in 1+1 dimensions) is a testbed for the study of quantum gauge field theories. We give scalable, explicit digital quantum algorithms to simulate the lattice Schwinger model in both NISQ and fault-tolerant settings. In particular, we perform a tight analysis of low-order Trotter formula simulations of the Schwinger model, using recently derived commutator bounds, and give upper bounds on the resources needed for simulations in both scenarios. In lattice units, we find a Schwinger model on N/2 physical sites with coupling constant x-1/2 and electric field cutoff x-1/2Λ can be simulated on a quantum computer for time 2xT using a number of T-gates or CNOTs in Õ(N3/2 T3/2 x1/2 Λ) for fixed operator error. This scaling with the truncation Λ is better than that expected from algorithms such as qubitization or QDRIFT. Furthermore, we give scalable measurement schemes and algorithms to estimate observables which we cost in both the NISQ and fault-tolerant settings by assuming a simple target observable—the mean pair density. Finally, we bound the root-mean-square error in estimating this observable via simulation as a function of the diamond distance between the ideal and actual CNOT channels. This work provides a rigorous analysis of simulating the Schwinger model, while also providing benchmarks against which subsequent simulation algorithms can be tested.
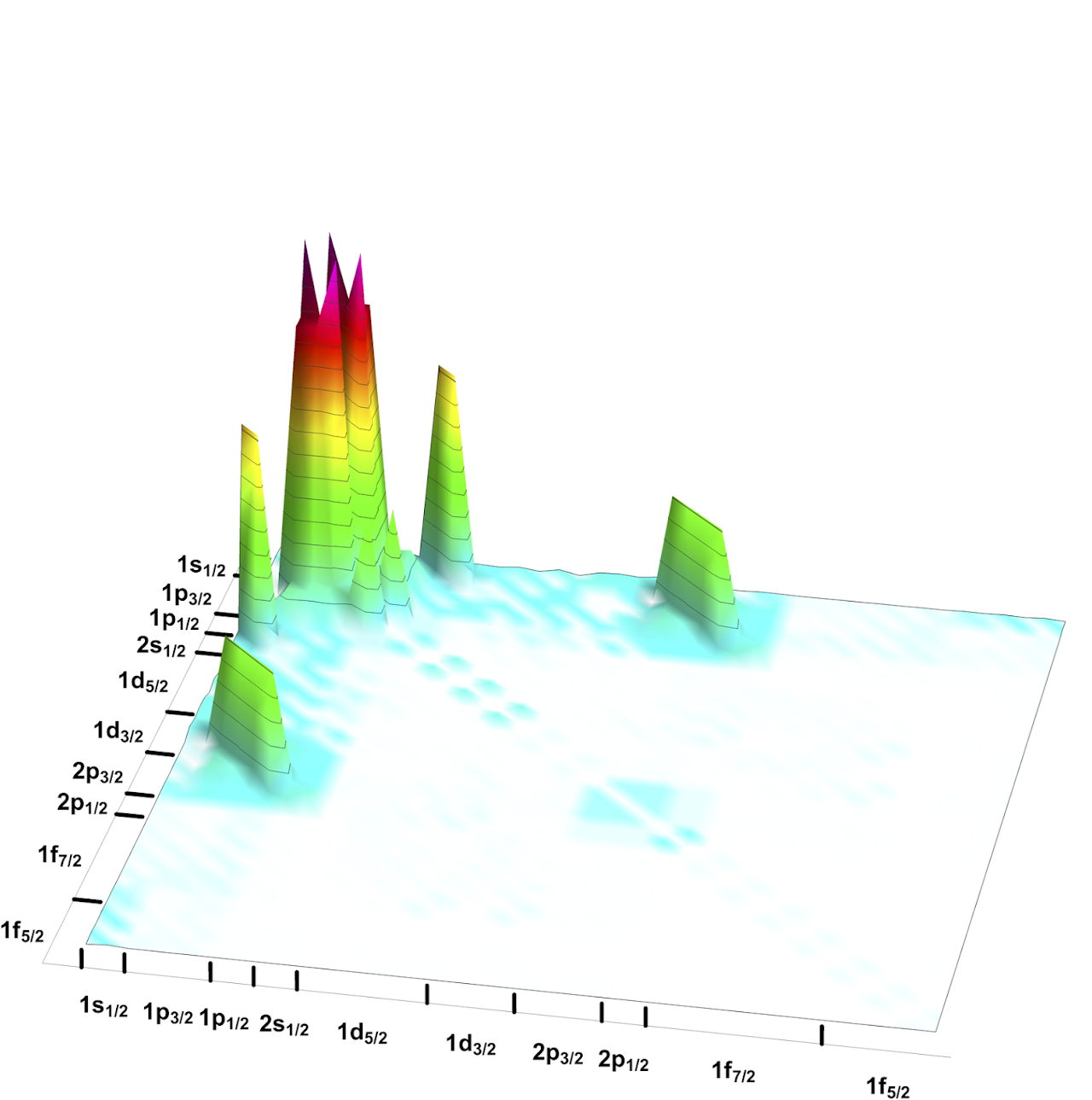
Entanglement Rearrangement in Self-Consistent Nuclear Structure Calculations
Entanglement properties of 4He and 6He are investigated using nuclear many-body calculations, specifically the single-nucleon entanglement entropy, and the two-nucleon mutual information and negativity. Nuclear wavefunctions are obtained by performing active-space no-core configuration interaction calculations using a two-body nucleon-nucleon interaction derived from chiral effective field theory. Entanglement measures within single-particle bases, the harmonic oscillator (HO), Hartree-Fock (HF), natural (NAT) and variational natural (VNAT) bases, are found to exhibit different degrees of complexity. Entanglement in both nuclei is found to be more localized within NAT and VNAT bases than within a HO basis for the optimal HO parameters, and, as anticipated, a core-valence (tensor product) structure emerges from the full six-body calculation of 6He. The two-nucleon mutual information shows that the VNAT basis, which typically exhibits good convergence properties, effectively decouples the active and inactive spaces. We conclude that measures of one- and two-nucleon entanglement are useful in analyzing the structure of nuclear wave functions, in particular the efficacy of basis states, and may provide useful metrics toward developing more efficient schemes for ab initio computations of the structure and reactions of nuclei, and quantum many-body systems more generally.
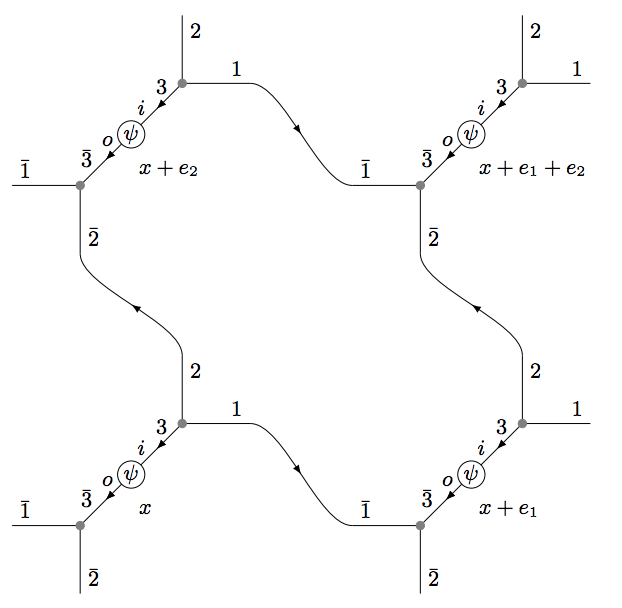
Loop, String, and Hadron Dynamics in SU(2) Hamiltonian Lattice Gauge Theories
The question of how to efficiently formulate Hamiltonian gauge theories is experiencing renewed interest due to advances in building quantum simulation platforms. We introduce a reformulation of an SU(2) Hamiltonian lattice gauge theory—a loop-string-hadron (LSH) formulation—that describes dynamics directly in terms of its loop, string, and hadron degrees of freedom, while alleviating several disadvantages of quantum-simulating the Kogut-Susskind formulation. This LSH formulation transcends the local loop formulation of d+1-dimensional lattice gauge theories by incorporating staggered quarks, furnishing the algebra of gauge-singlet operators, and being used to reconstruct dynamics between states that have Gauss’s law built in to them. LSH operators are then factored into products of “normalized” ladder operators and diagonal matrices, priming them for classical or quantum information processing. Self-contained expressions of the Hamiltonian are given up to d=3. The LSH formalism uses makes little use of structures specific to SU(2) and its conceptual clarity makes it an attractive approach to apply to other non-Abelian groups like SU(3).
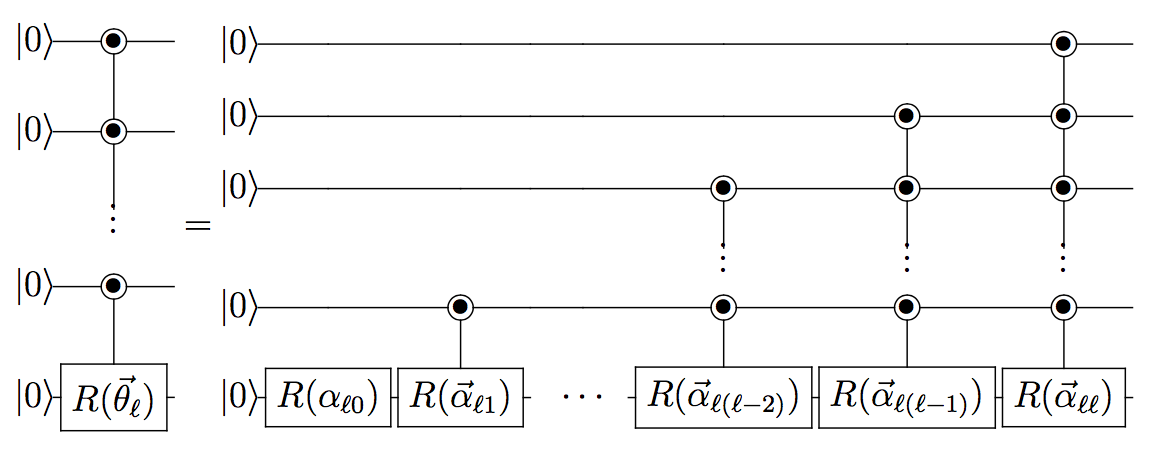
Systematically Localizable Operators for Quantum Simulations of Quantum Field Theories
Correlations and measures of entanglement in ground state wavefunctions of relativistic quantum field theories are spatially localized over length scales set by the mass of the lightest particle. We utilize this localization to design digital quantum circuits for preparing the ground states of free lattice scalar quantum field theories. Controlled rotations that are exponentially localized in their position-space extent are found to provide exponentially convergent wavefunction fidelity. These angles scale with the classical two-point correlation function, as opposed to the more localized mutual information or the hyper-localized negativity. We anticipate that further investigations will uncover quantum circuit designs with controlled rotations dictated by the measures of entanglement. This work is expected to impact quantum simulations of systems of importance to nuclear physics, high-energy physics, and basic energy sciences research.
Fixed-Point Quantum Circuits for Quantum Field Theories
Renormalization group ideas and effective operators are used to efficiently determine localized unitaries for preparing the ground states of non-interacting scalar field theories on digital quantum devices. With these methods, classically computed ground states in a small spatial volume can be used to determine operators for preparing the ground state in a beyond-classical quantum register, even for interacting scalar field theories. Due to the exponential decay of correlation functions and the double exponential suppression of digitization artifacts, the derived quantum circuits are expected to be relevant already for near-term quantum devices.
Quantum Computer Systems for Scientific Discovery
The great promise of quantum computers comes with the dual challenges of building them and finding their useful applications. We argue that these two challenges should be considered together, by co-designing full-stack quantum computer systems along with their applications in order to hasten their development and potential for scientific discovery. In this context, we identify scientific and community needs, opportunities, a sampling of a few use case studies, and significant challenges for the development of quantum computers for science over the next 2–10 years. This document is written by a community of university, national laboratory, and industrial researchers in the field of Quantum Information Science and Technology, and is based on a summary from a U.S. National Science Foundation workshop on Quantum Computing held on October 21–22, 2019 in Alexandria, VA.
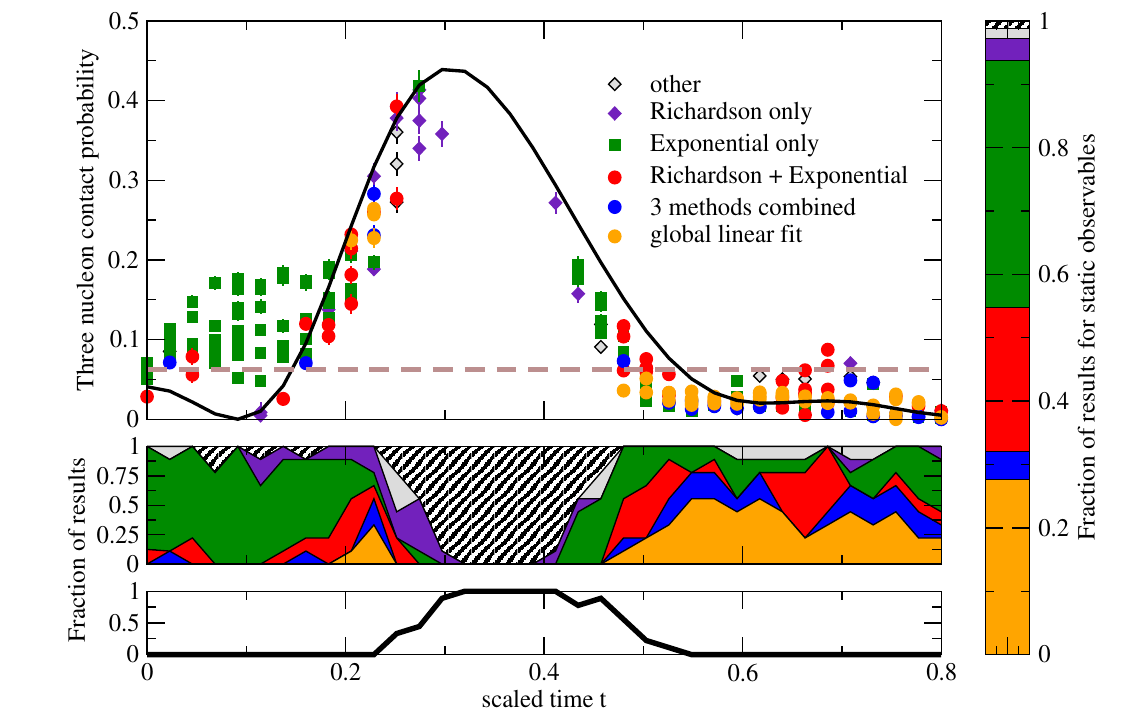
Quantum Computing for Neutrino-nucleus Scattering
Neutrino-nucleus cross section uncertainties are expected to be a dominant systematic in future accelerator neutrino experiments. The cross sections are determined by the linear response of the nucleus to the weak interactions of the neutrino, and are dominated by energy and distance scales of the order of the separation between nucleons in the nucleus. These response functions are potentially an important early physics application of quantum computers. Here we present an analysis of the resources required and their expected scaling for scattering cross section calculations. We also examine simple small-scale neutrino-nucleus models on modern quantum hardware. In this paper, we use variational methods to obtain the ground state of a three nucleon system (the triton) and then implement the relevant time evolution. In order to tame the errors in present-day NISQ devices, we explore the use of different error-mitigation techniques to increase the fidelity of the calculations.
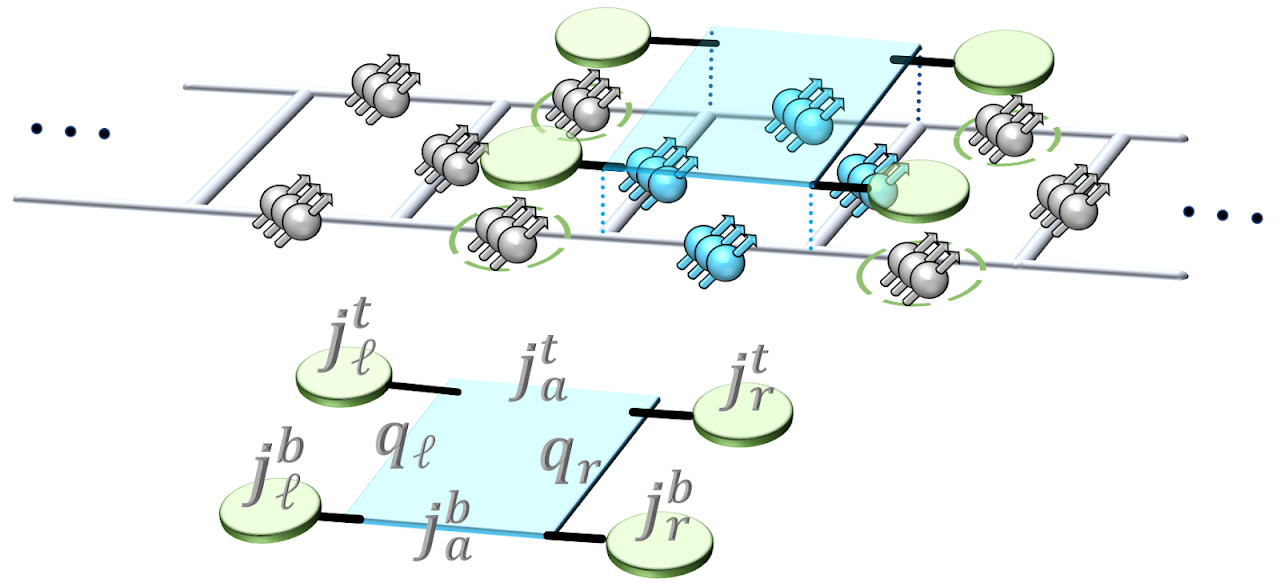
SU(2) Non-Abelian Gauge Field Theory in One Dimension on Digital Quantum Computers
An improved mapping of one-dimensional SU(2) non-Abelian gauge theory onto qubit degrees of freedom is presented. This new mapping allows for a reduced unphysical Hilbert space. Insensitivity to interactions within this unphysical space is exploited to design more efficient quantum circuits. Local gauge symmetry is used to analytically incorporate the angular momentum alignment, leading to qubit registers encoding the total angular momentum on each link. Results of multi-plaquette calculations on IBM’s quantum hardware are presented.
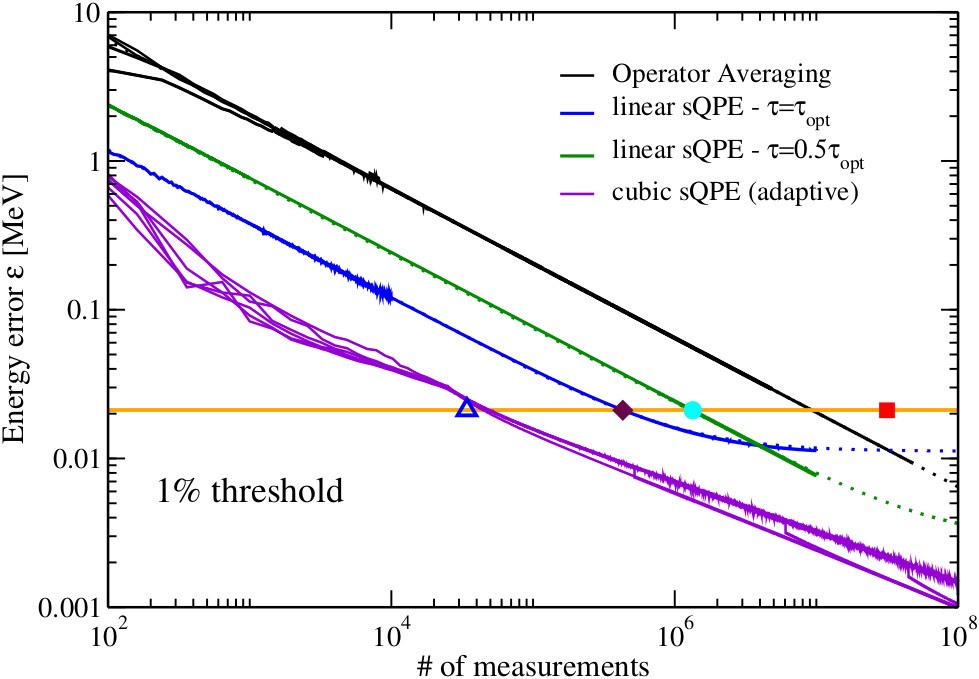
Short-depth circuits for efficient expectation value estimation
The evaluation of expectation values Tr[ρO] for some pure state ρ and Hermitian operator O is of central importance in a variety of quantum algorithms. Near optimal techniques developed in the past require a number of measurements N approaching the Heisenberg limit N=O(1/ϵ) as a function of target accuracy ϵ. The use of Quantum Phase Estimation requires however long circuit depths C=O(1/ϵ) making their implementation difficult on near term noisy devices. The more direct strategy of Operator Averaging is usually preferred as it can be performed using N=O(1/ϵ2) measurements and no additional gates besides those needed for the state preparation. In this work we use a simple but realistic model to describe the bound state of a neutron and a proton (the deuteron) and show that the latter strategy can require an overly large number of measurement in order to achieve a reasonably small relative target accuracy ϵr. We propose to overcome this problem using a single step of QPE and classical post-processing. This approach leads to a circuit depth C=O(ϵm) (with m≥0) and to a number of measurements N=O(1/ϵ2+n) for 0<n≤1. We provide detailed descriptions of two implementations of our strategy for n=1 and n≈0.5 and derive appropriate conditions that a particular problem instance has to satisfy in order for our method to provide an advantage.
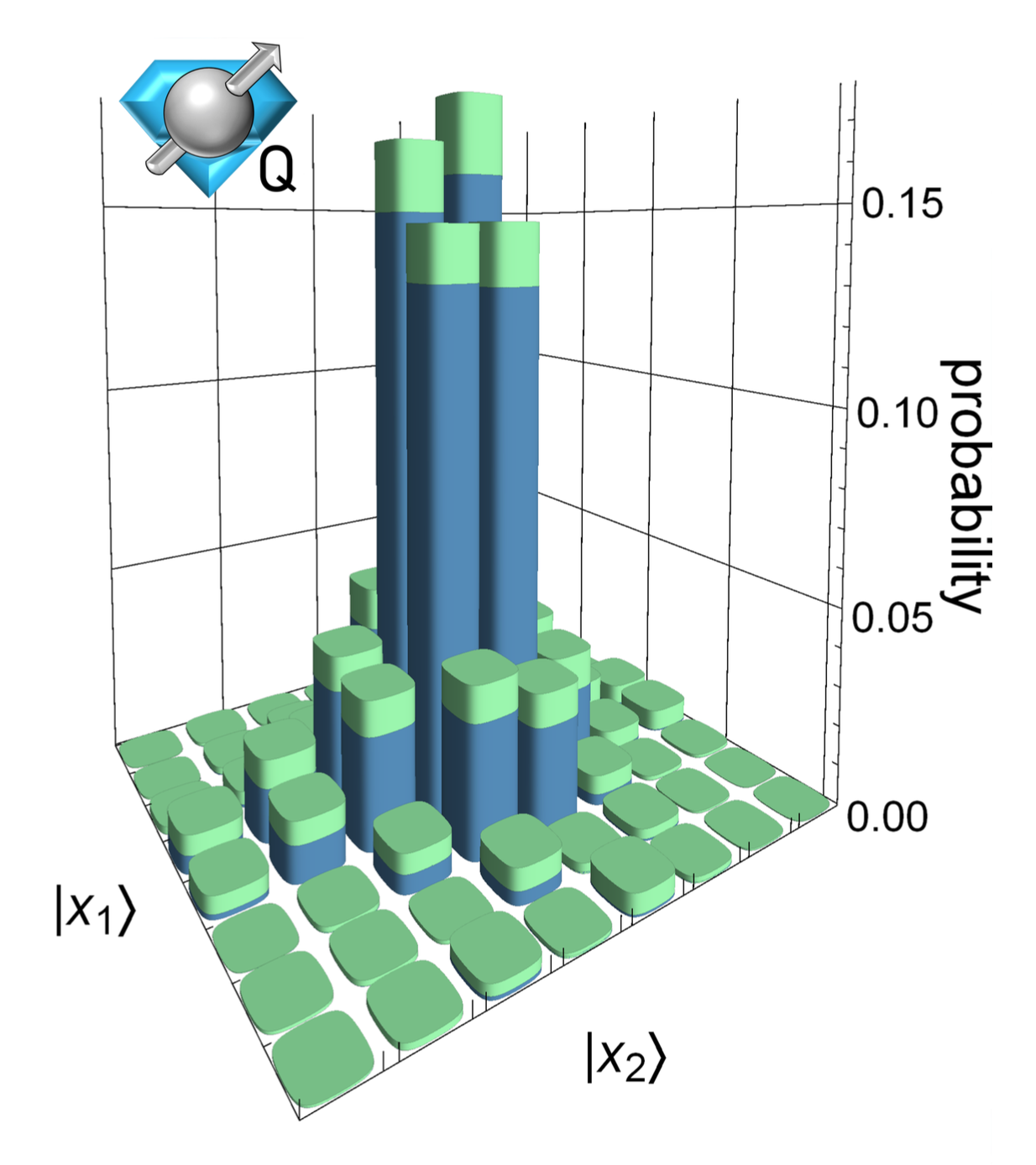
Minimally-Entangled State Preparation of Localized Wavefunctions on Quantum Computers
Initializing a single site of a lattice scalar field theory into an arbitrary state requires O(2nQ) entangling gates on a quantum computer with nQ qubits per site. It is conceivable that, instead, initializing to functions that are good approximations to states may have utility in reducing the number of required entangling gates. In the case of a single site of a non-interacting scalar field theory, initializing to a symmetric exponential wavefunction requires nQ − 1 entangling gates, compared with the 2nQ−1 + nQ − 3 + δnQ,1 required for a symmetric Gaussian wavefunction. In this work, we explore the initialization of 1-site (nQ = 4), 2-site (nQ = 3) and 3-site (nQ = 3) non- interacting scalar field theories with symmetric exponential wavefunctions using IBM’s quantum simulators and quantum devices (Poughkeepsie and Tokyo). With the digitizations obtainable with nQ = 3, 4, these tensor-product wavefunctions are found to have large overlap with a Gaussian wavefunction, and provide a suitable low-noise initialization for subsequent quantum simulations. In performing these simulations, we have employed a workflow that interleaves calibrations to mitigate systematic errors in production. The calibrations allow tolerance cuts on gate performance including the fidelity of the symmetrizing Hadamard gate, both in vacuum (|0⟩⊗nQ ) and in medium (nQ − 1 qubits initialized to an exponential function). The results obtained in this work are relevant to systems beyond scalar field theories, such as the deuteron radial wavefunction, 2- and 3-dimensional cartesian-space wavefunctions, and non-relativistic multi-nucleon systems built on a localized eigenbasis.
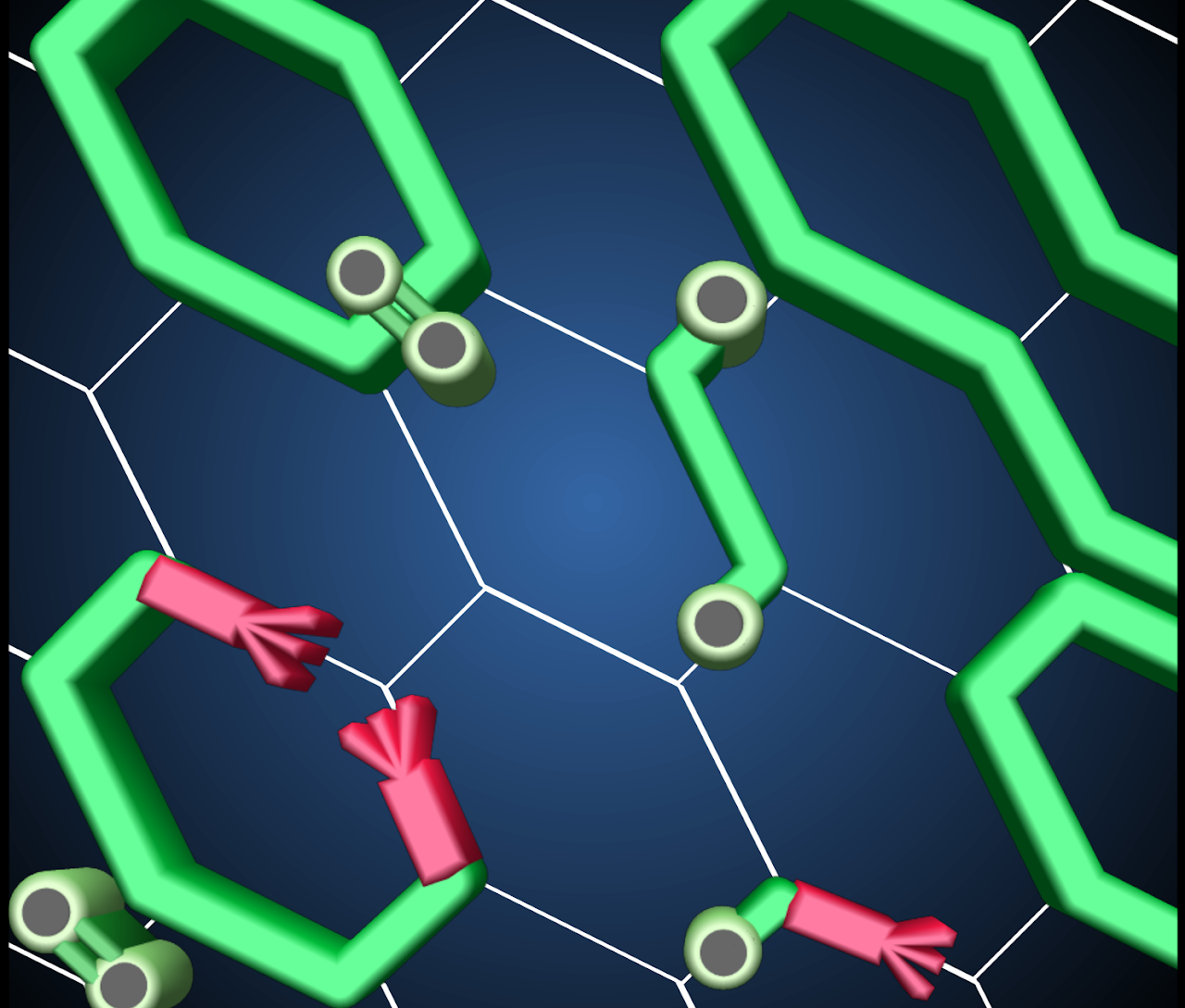
Solving Gauss’s Law on Digital Quantum Computers with Loop-String-Hadron Digitization
We show that using the loop-string-hadron (LSH) formulation of SU(2) lattice gauge theory (arXiv:1912.06133) as a basis for digital quantum computation easily solves an important problem of fundamental interest: implementing gauge invariance (or Gauss’s law) exactly. We first discuss the structure of the LSH Hilbert space in d spatial dimensions, its truncation, and its digitization with qubits. Error detection and mitigation in gauge theory simulations would benefit from physicality “oracles,” so we decompose circuits that flag gauge invariant wavefunctions. We then analyze the logical qubit costs and entangling gate counts involved with the protocols. The LSH basis could save or cost more qubits than a Kogut-Susskind-type representation basis, depending on how that is digitized as well as the spatial dimension. The numerous other clear benefits encourage future studies into applying this framework.
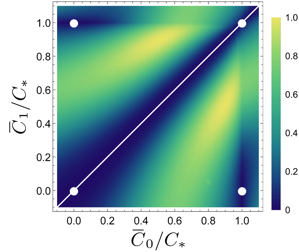
Entanglement Suppression and Emergent Symmetries of Strong Interactions
Entanglement suppression in the strong interaction S-matrix is shown to be correlated with approximate spin-flavor symmetries that are observed in low-energy baryon interactions, the Wigner SU(4) symmetry for two flavors and an SU(16) symmetry for three flavors. We conjecture that dynamical entanglement suppression is a property of the strong interactions in the infrared, giving rise to these emergent symmetries and providing powerful constraints on the nature of nuclear and hypernuclear forces in dense matter.
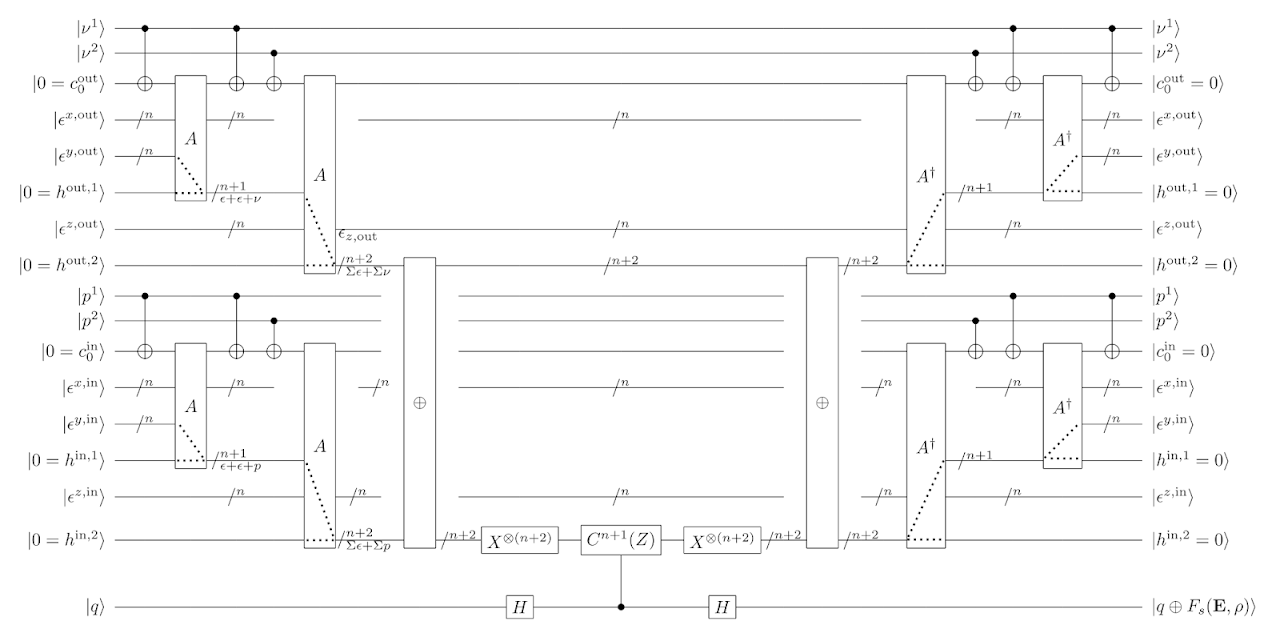
Oracles for Gauss’s Law on Digital Quantum Computers
Formulating a lattice gauge theory using only physical degrees of freedom generically leads to non-local interactions. A local Hamiltonian is desirable for quantum simulation, and this is possible by treating the Hilbert space as a subspace of a much larger Hilbert space in which Gauss’s law is not automatic. Digital quantum simulations of this local formulation will wander into unphysical sectors due to errors from Trotterization or from quantum noise. In this work, oracles are constructed that use local Gauss law constraints to projectively distinguish physical and unphysical wave functions in Abelian lattice gauge theories. Such oracles can be used to detect errors that break Gauss’s law.
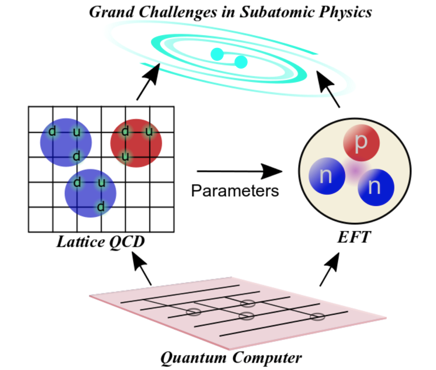
Simulations of Subatomic Many-Body Physics on a Quantum Frequency Processor
Simulating complex many-body quantum phenomena is a major scientific impetus behind the development of quantum computing, and a range of technologies are being explored to address such systems. We present the results of the largest photonics-based simulation to date, applied in the context of subatomic physics. Using an all-optical quantum frequency processor, the ground-state energies of light nuclei including the triton (3H), 3He, and the alpha particle (4He) are computed. Complementing these calculations and utilizing a 68-dimensional Hilbert space, our photonic simulator is used to perform sub-nucleon calculations of the two-body and three-body forces between heavy mesons in the Schwinger model. This work is a first step in simulating subatomic many-body physics on quantum frequency processors—augmenting classical computations that bridge scales from quarks to nuclei.[Image (left) was created by Pavel Lougovski.]
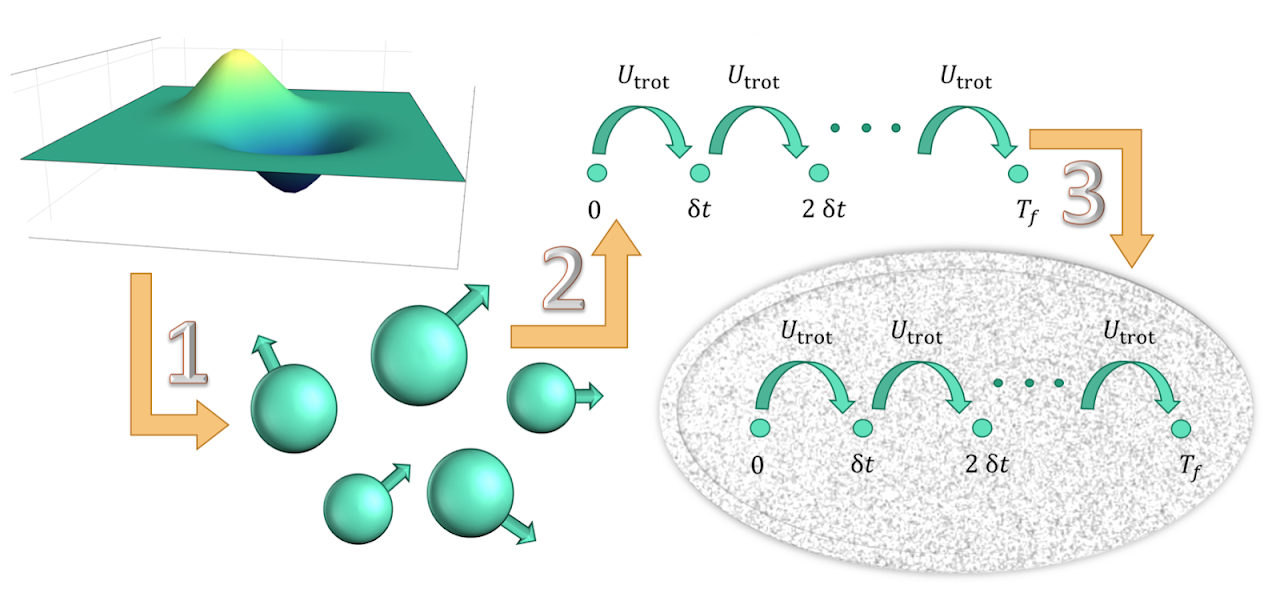
Digitization of Scalar Fields for NISQ-Era Quantum Computing
Qubit, operator and gate resources required for the digitization of lattice λϕ4 scalar field theories onto quantum computers in the NISQ era are considered, building upon the foundational work by Jordan, Lee and Preskill. The Nyquist-Shannon sampling theorem, introduced in this context by Macridin, Spetzouris, Amundson and Harnik building on the work of Somma, provides a guide with which to evaluate the efficacy of two field-space bases, the eigenstates of the field operator, as used by Jordan, Lee and Preskill, and eigenstates of a harmonic oscillator, to describe 0+1- and 1+1-dimensional scalar field theory. We show how techniques associated with improved actions, which are heavily utilized in Lattice QCD calculations to systematically reduce lattice-spacing artifacts, can be used to reduce the impact of the field digitization in λϕ4, but are found to be inferior to a complete digitization-improvement of the Hamiltonian using a Quantum Fourier Transform. When the Nyquist-Shannon sampling theorem is satisfied, digitization errors scale as |log|log|ϵdig|||∼nQ (number of qubits describing the field at a given spatial site) for the low-lying states, leaving the familiar power-law lattice-spacing and finite-volume effects that scale as |log|ϵlatt||∼NQ (total number of qubits in the simulation). We find that fewer than nQ=10 qubits per spatial lattice site are sufficient to reduce digitization errors below noise levels expected in NISQ-era quantum devices for both localized and delocalized field-space wavefunctions. For localized wavefunctions, nQ=4 qubits are likely to be sufficient for calculations requiring modest precision.
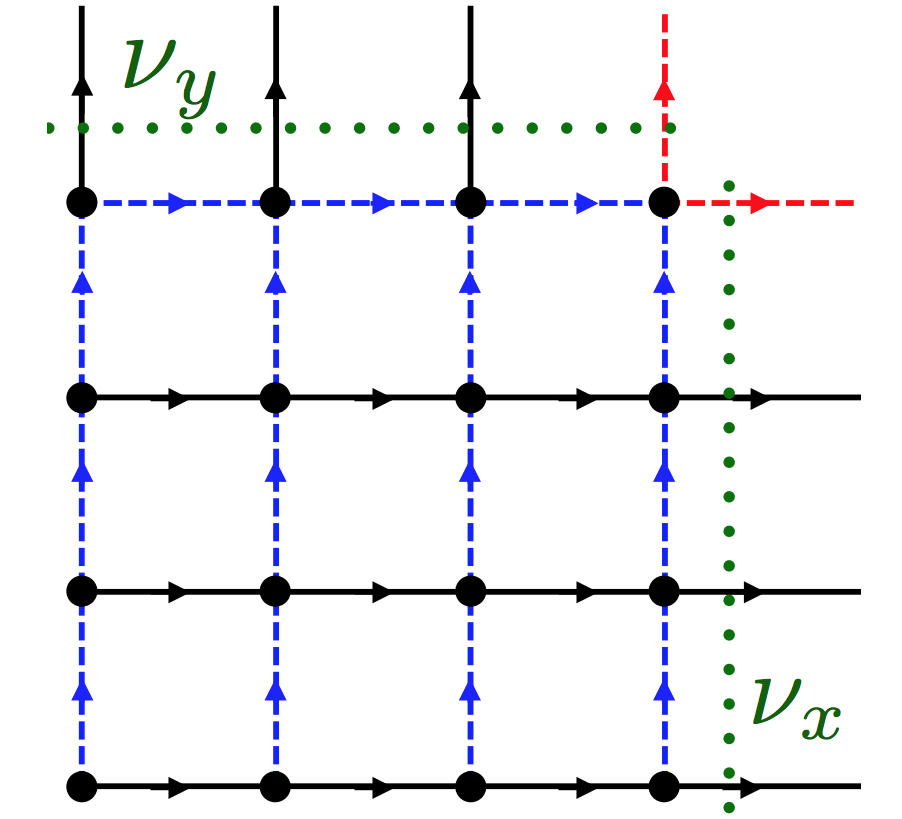
Gauss’s Law, Duality, and the Hamiltonian Formulation of U(1) Lattice Gauge Theory
Quantum computers have the potential to explore the vast Hilbert space of entangled states that play an important role in the behavior of strongly interacting matter. This opportunity motivates reconsidering the Hamiltonian formulation of gauge theories, with a suitable truncation scheme to render the Hilbert space finite-dimensional. Conventional formulations lead to a Hilbert space largely spanned by unphysical states; given the current inability to perform large scale quantum computations, we examine here how one might restrict wave function evolution entirely or mostly to the physical subspace. We consider such constructions for the simplest of these theories containing dynamical gauge bosons—U(1) lattice gauge theory without matter in d=2,3 spatial dimensions—and find that electric-magnetic duality naturally plays an important role. We conclude that this approach is likely to significantly reduce computational overhead in d=2 by a reduction of variables and by allowing one to regulate magnetic fluctuations instead of electric. The former advantage does not exist in d=3, but the latter might be important for asymptotically-free gauge theories.
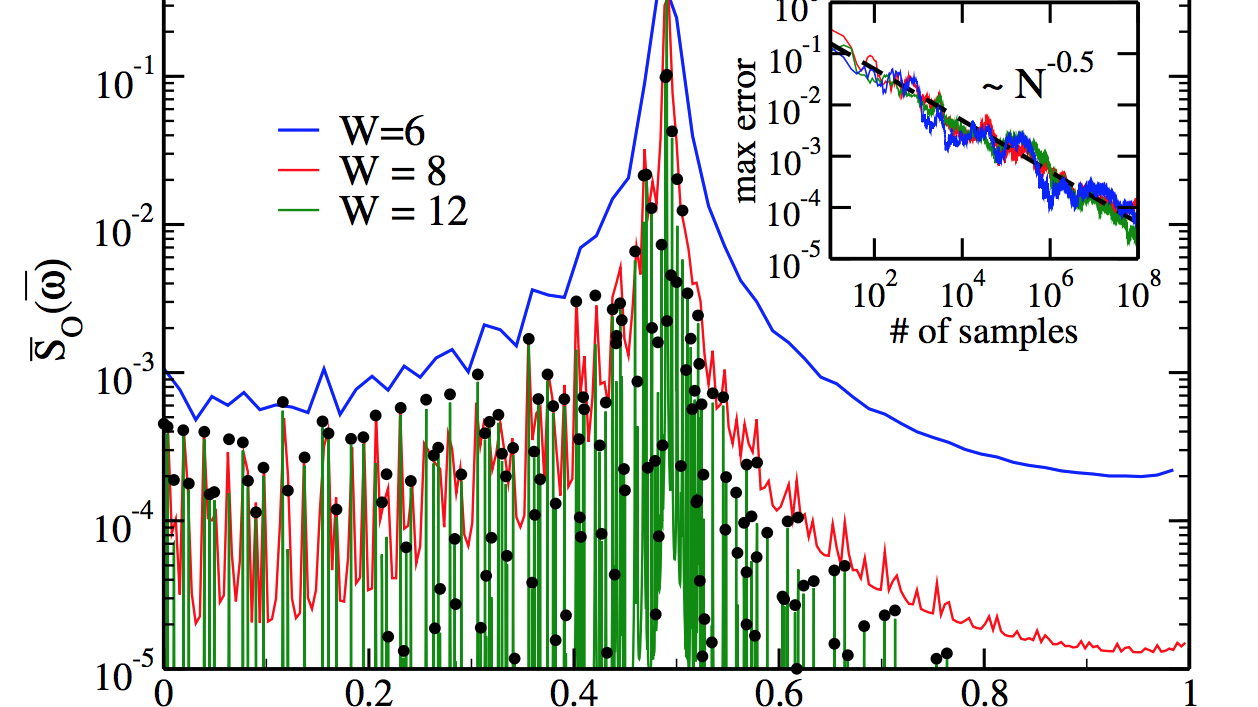
Linear Response on a Quantum Computer
The dynamic linear response of a quantum system is critical for understanding both the structure and dynamics of strongly-interacting quantum systems, including neutron scattering from materials, photon and electron scattering from atomic systems, and electron and neutrino scattering by nuclei. We present a general algorithm for quantum computers to calculate the dynamic linear response function with controlled errors and to obtain information about specific final states that can be directly compared to experimental observations.
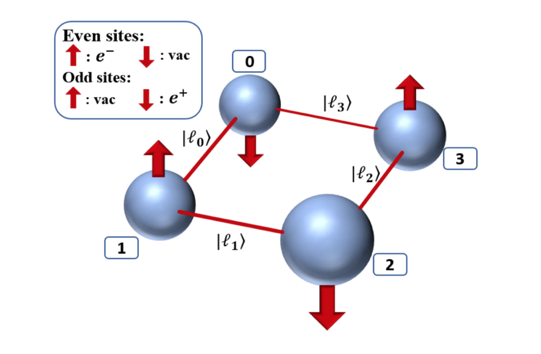
Quantum-classical computation of Schwinger model dynamics using quantum computers
We present a quantum-classical algorithm to study the dynamics of the two-spatial-site Schwinger model on IBM’s quantum computers. Using rotational symmetries, total charge, and parity, the number of qubits needed to perform computation is reduced by a factor of ∼5, removing exponentially-large unphysical sectors from the Hilbert space. Our work opens an avenue for exploration of other lattice quantum field theories, such as quantum chromodynamics, where classical computation is used to find symmetry sectors in which the quantum computer evaluates the dynamics of quantum fluctuations.
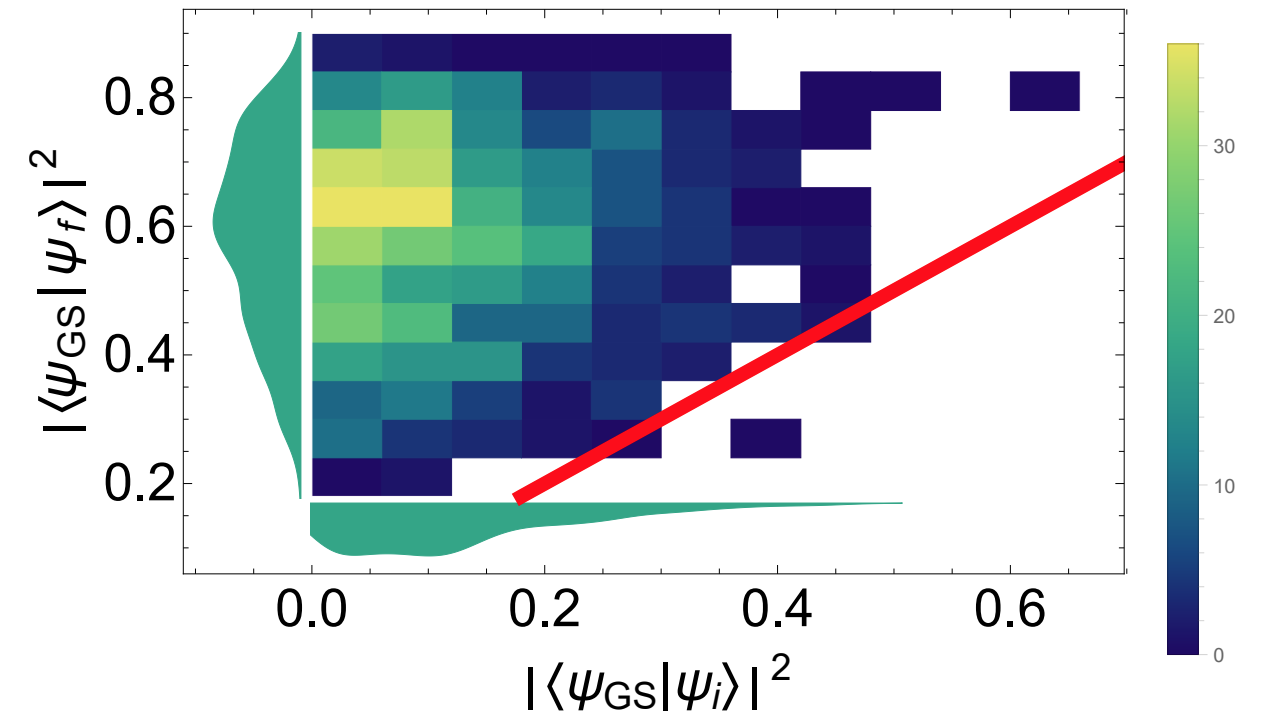
Ground States via Spectral Combing on a Quantum Computer
A new method is proposed for determining the ground state wave function of a quantum many-body system on a quantum computer, without requiring an initial trial wave function that has good overlap with the true ground state. The technique of Spectral Combing involves entangling an arbitrary initial wave function with a set of auxiliary qubits governed by a time dependent Hamiltonian, resonantly transferring energy out of the initial state through a plethora of avoided level crossings into the auxiliary system. The number of avoided level crossings grows exponentially with the number of qubits required to represent the Hamiltonian, so that the efficiency of the algorithm does not rely on any particular energy gap being large. We give an explicit construction of the quantum gates required for the realization of this procedure and explore the results of classical simulations of the algorithm on a small quantum computer with up to 8 qubits. We show that for certain systems and comparable results, Spectral Combing requires fewer quantum gates to realize than the Quantum Adiabatic Algorithm.


