IQuS Publications
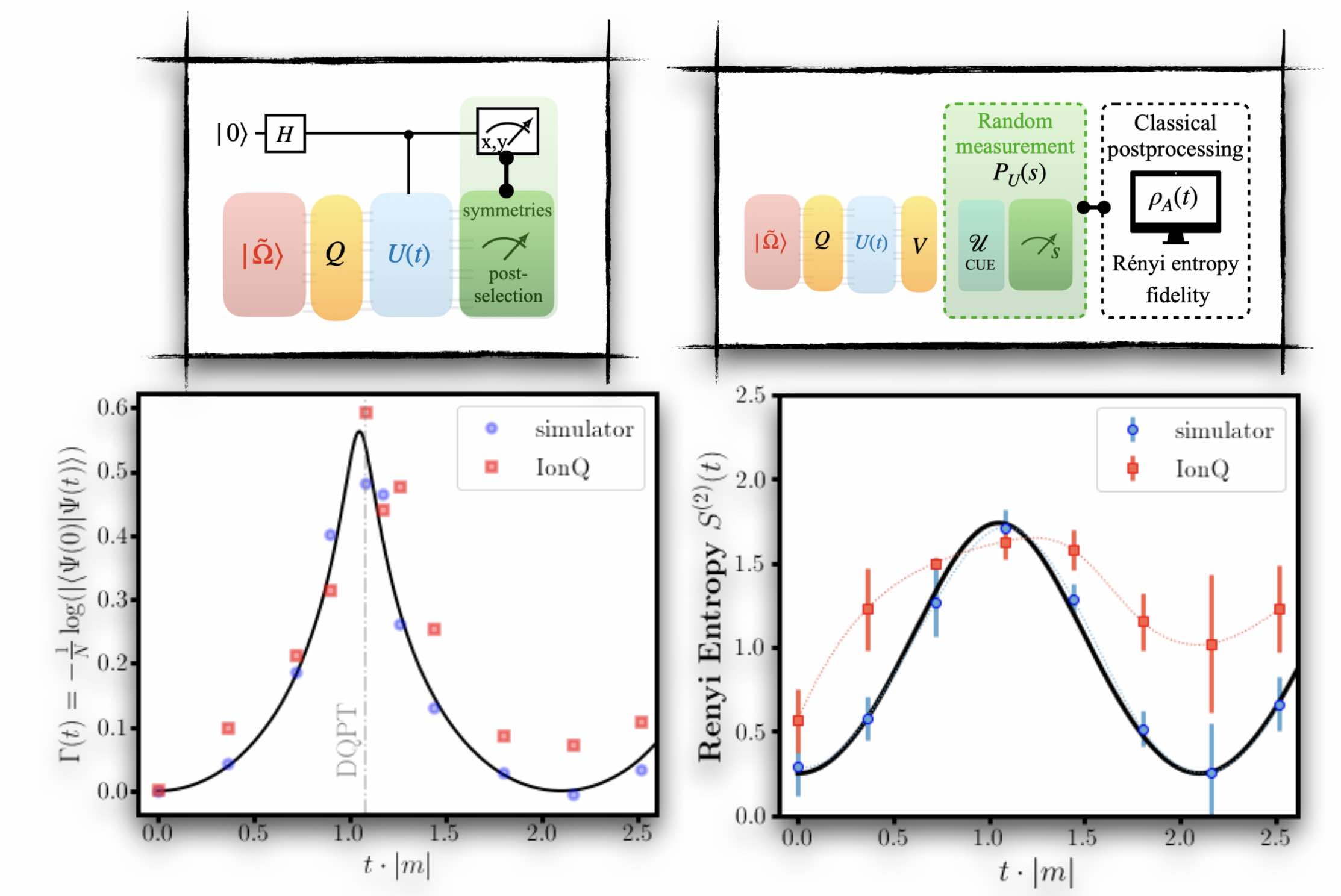
Quantum computation of dynamical quantum phase transitions and entanglement tomography in a lattice gauge theory
Strongly-coupled gauge theories far from equilibrium may exhibit unique features that could illuminate the physics of early universe and of hadron and ion colliders. Studying real-time phenomena has proven challenging with classical-simulation methods, but is a natural application of quantum-simulation devices. To demonstrate this prospect, we quantum compute non-equal time correlation functions and perform entanglement tomography of non-equilibrium states of a simple lattice gauge theory, the Schwinger model, using a trapped-ion quantum computer by IonQ Inc. As an ideal target for near-term devices, a recently-predicted dynamical quantum phase transition in this model is studied by preparing, quenching, and tracking the subsequent non-equilibrium dynamics in three ways: i) overlap echos signaling dynamical transitions, ii) non-equal time correlation functions with an underlying topological nature, and iii) the entanglement structure of non-equilibrium states, including Entanglement Hamiltonians. These results constitute the first observation of a dynamical quantum phase transition in a lattice gauge theory on a quantum computer, and are a first step toward investigating topological phenomena in nuclear and high-energy physics using quantum technologies.
Lattice regularization of Theta-vacua in Grassmannian nonlinear sigma models: Anomalies, sign-problems and qubit models
Anomalies are a powerful way to gain insight into possible lattice regularizations of a quantum field theory. In this work, we consider lattice regularizations of a class of the toy-models of QCD: the 1+1-dimensional asymptotically-free Grassmanian nonlinear sigma models with a theta term. We argue that the continuum anomaly for a given symmetry can be matched by a manifestly symmetric lattice regularization only if (i) the symmetry action is offsite, or (ii) if the continuum anomaly is reproduced exactly on the lattice. Using the Grassmanian nonlinear sigma models as a case study, we provide examples of lattice regularizations in which both possibilities are realized. For possibility (i), we generalize recent work for the O(3) NLSM with an arbitrary theta term, where it was regulated using model of qubits with a small extra dimension, solving a sign problem present in conventional formulations of theta vacua. We argue that Grassmannian NLSM can be obtained similarly from SU(N) antiferromagnets with a well-defined continuum limit, reproducing both the IR physics of theta vacua and the UV physics of asymptotic freedom. These results enable the application of new classical algorithms to lattice Monte Carlo studies of these quantum field theories, and provide a viable realization suited for their quantum simulation. On the other hand, we show that, perhaps surprisingly, the conventional lattice regularization of theta vacua due to Berg and Luscher reproduces the anomaly exactly on the lattice, providing a realization of the second possibility.
Preparations for Quantum Simulations of Quantum Chromodynamics in 1+1 Dimensions: (II) Single-Baryon Beta-Decay in Real Time
A framework for quantum simulations of real-time weak decays of hadrons and nuclei in a 2-flavor lattice theory in one spatial dimension is presented. A single generation of the Standard Model is mapped to spin operators via the Jordan-Wigner transformation, and both quantum chromodynamics and flavor-changing weak interactions are included in the dynamics, the latter through four-Fermi effective operators. This mapping requires 16 qubits per spatial lattice site. Quantum circuits which implement time evolution in this lattice theory are developed and run on Quantinuum’s H1 1 20-qubit trapped ion system to simulate the beta-decay of a single baryon on one lattice site. Simulations of the real-time evolution of a single baryon, including initial state preparation, are performed for both one and two Trotter time steps. We comment on the potential intrinsic error-correction properties of this type of lattice theory.
Branching States as The Emergent Structure of a Quantum Universe
Quantum Darwinism builds on decoherence theory to explain the emergence of classical behavior within a quantum universe. We demonstrate that the differential geometric underpinnings of quantum mechanics provide a uniquely informative window into the structure of correlations needed to validate quantum Darwinism. This leads us to two crucial insights about the emergence of classical phenomenology, centered around the nullity of quantum discord. First, we show that the so-called branching structure of the joint state of system and environment is the only one compatible with zero discord. Second, we prove that for small, but nonzero discord, the structure of the globally pure state is arbitrarily close to the branching form. These provide strong evidence that this class of branching states is the only one compatible with the emergence of classical phenomenology, as described in quantum Darwinism.
Simulating Heisenberg interactions in the Ising model with strong drive fields
The time-evolution of an Ising model with large driving fields over discrete time intervals is shown to be reproduced by an effective XXZ-Heisenberg model at leading order in the inverse field strength. For specific orientations of the drive field, the dynamics of the XXX-Heisenberg model is reproduced. These approximate equivalences, valid above a critical driving field strength set by dynamical phase transitions in the Ising model, are expected to enable quantum devices that natively evolve qubits according to the Ising model to simulate more complex systems.
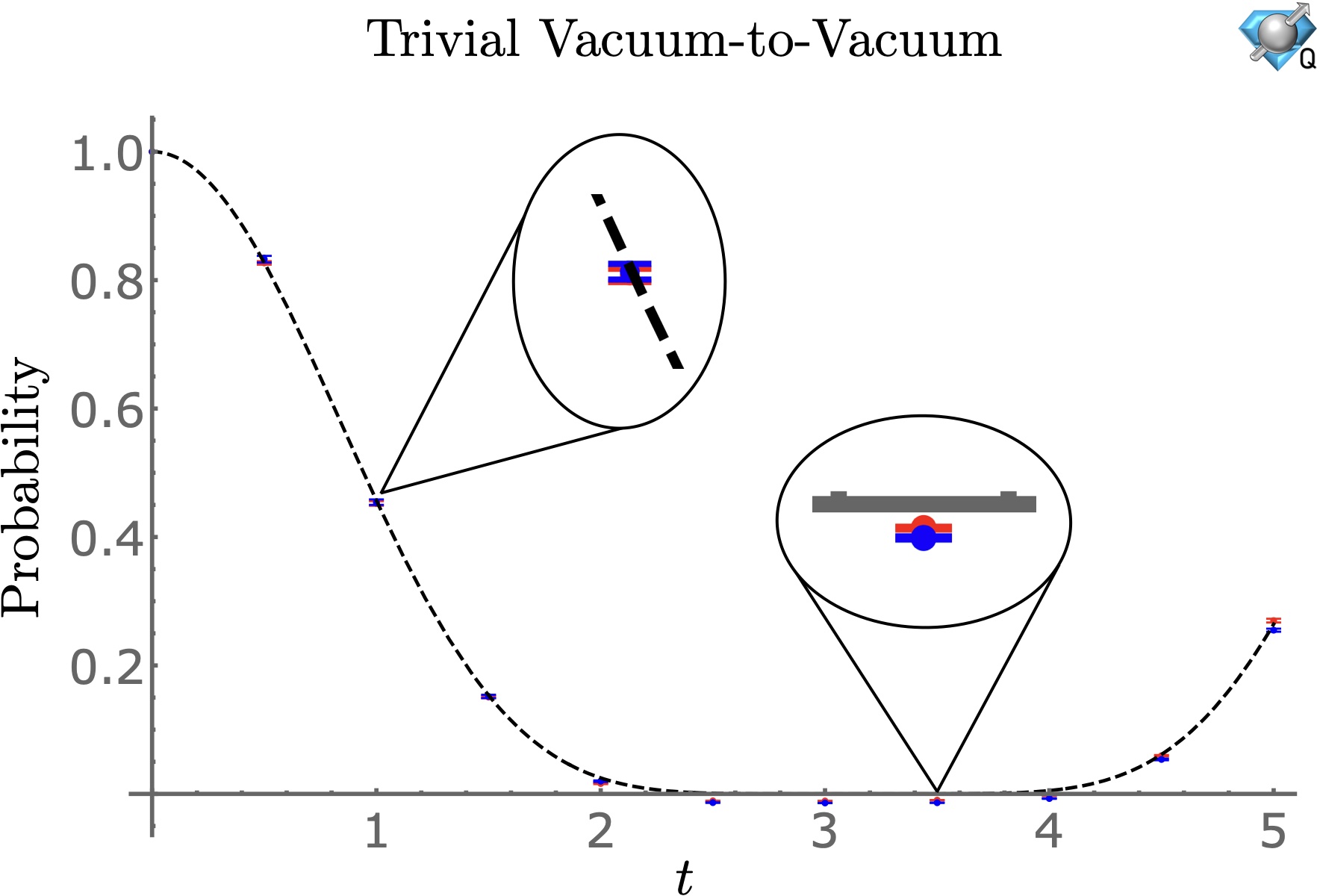
Preparations for Quantum Simulations of Quantum Chromodynamics in 1+1 Dimensions: (I) Axial Gauge
The resource requirements for quantum simulations of 1+1 dimensional quantum chromodynamics are estimated. When formulated in axial gauge and with two flavors of quarks, this system requires 12 qubits per spatial site once Gauss’s law has been enforced to uniquely constrain the gauge fields. Classical computations and D-Wave’s quantum annealer Advantage are used to determine the hadronic spectrum, enabling a decomposition of the masses and a study of quark entanglement. We identify color “edge” states, resulting from open boundary conditions, that are confined within a screening length to the end of the lattice. Quantum circuits for the time evolution of SU(Nc) gauge theory with Nf flavors of quarks are developed and used to determine the resources required for large-scale quantum simulations. IBM’s 7-qubit quantum computers ibmq_jakarta and ibm_perth were used to compute the trivial vacuum-to-vacuum and trivial vacuum-to-qr qr bar probabilities in Nf=1 QCD with one spatial site from one Trotter step of the time-evolution operator.
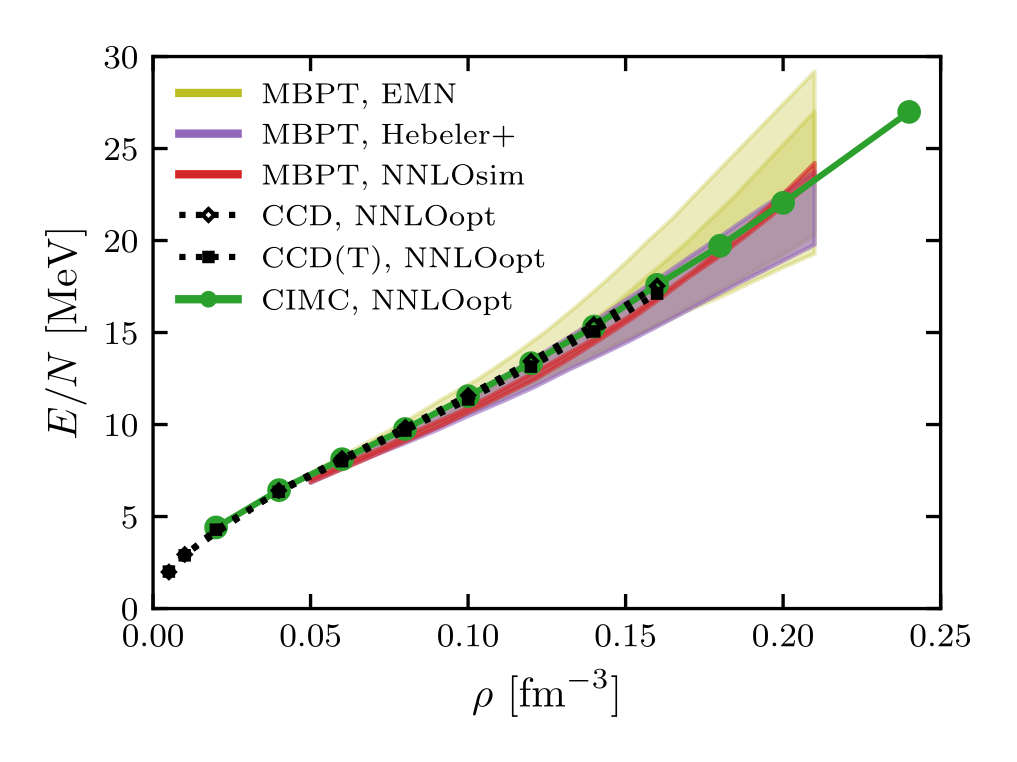
Quantum Monte Carlo in Configuration Space with Three-Nucleon Forces
Neutron matter, through its connection to neutron stars as well as systems like cold atom gases, is one of the most interesting yet accessible systems in nuclear physics. The Configuration-Interaction Monte Carlo (CIMC) method is a stochastic many-body technique allowing to tackle strongly coupled systems. In contrast to other Quantum Monte Carlo methods employed in nuclear physics, the CIMC method can be formulated directly in momentum space allowing for an efficient use of non-local interactions.
In this work we extend CIMC method to include three-nucleon interactions through the normal-ordered two-body approximation. We present results for the equation of state of neutron matter in line with other many-body calculations with low resolution chiral interactions, and provide predictions for the momentum distribution and the static structure factor.

Snowmass Computational Frontier: Topical Group Report on Quantum Computing
Quantum computing will play a pivotal role in the High Energy Physics (HEP) science program over the early parts of the Twenty First Century, both as a major expansion of our capabilities across the Computational Frontier, and in synthesis with quantum sensing and quantum networks. This report outlines how Quantum Information Science (QIS) and HEP are deeply intertwined endeavors that benefit enormously from a strong engagement together.
A number of problems ranging from simulation of quantum field theories, to fully leveraging the most sensitive sensor suites for new particle searches, and even data analysis will run into limiting bottlenecks if constrained to our current computing paradigms. Easy early access to quantum computers is needed to build a deeper understanding of these connections and the opportunities for advancement. In turn, HEP brings crucial expertise to the national quantum ecosystem in quantum domain knowledge, materials science, cryogenic and fast electronics, and massive-scale project management. The role of quantum technologies across the entire economy and society at large is expected to grow rapidly over the next decade, so it is important to establish the role of HEP in the efforts surrounding QIS. Fully delivering on the promise of quantum technologies and the goals of the HEP science program requires robust support. It is important to invest in the co-design opportunities afforded by the broader quantum computing ecosystem by leveraging HEP strengths in QIS for materials, electronics, and theory with the goal of designing quantum computers tailored to HEP science.

Quantum Simulation for High-energy Physics
It is for the first time that quantum simulation for high-energy physics (HEP) is studied in the U.S. decadal particle-physics community planning, and in fact until recently, this was not considered a mainstream topic in the community. This fact speaks of a remarkable rate of growth of this subfield over the past few years, stimulated by the impressive advancements in quantum-information sciences (QIS) and associated technologies over the past decade, and the significant investment in this area by the government and private sectors in the U.S. and other countries. High-energy physicists have quickly identified problems of importance to our understanding of nature at the most fundamental level, from tiniest distances to cosmological extents, that are intractable with classical computers but may benefit from quantum advantage. They have initiated, and continue to carry out, a vigorous program in theory, algorithm, and hardware co-design for simulations of relevance to the HEP mission. This community whitepaper is an attempt to bring this exciting and yet challenging area of research to the spotlight, and to elaborate on what the promises, requirements, challenges, and potential solutions are over the next decade and beyond.
This whitepaper is prepared for the topical groups CompF6 (Quantum computing), TF05 (Lattice Gauge Theory), and TF10 (Quantum Information Science) within the Computational Frontier and Theory Frontier of the U.S. Community Study on the Future of Particle Physics (Snowmass 2021).
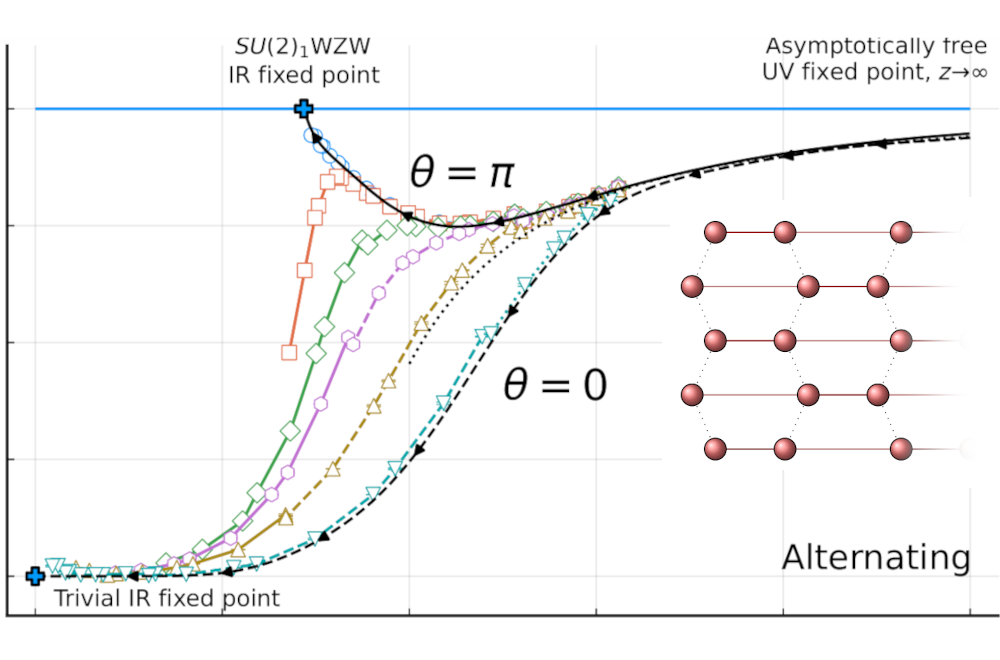
From Asymptotic Freedom to Theta Vacua: Qubit Embeddings of the O(3) Nonlinear Sigma Model
Conventional lattice formulations of $\theta$ vacua in the $1+1$-dimensional $O(3)$ nonlinear sigma model suffer from a sign problem. Here, we construct the first sign-problem-free regularization for \emph{arbitrary} $\theta$. Using efficient lattice \ac{MC} computations, we demonstrate how a Hamiltonian model of spin-$\tfrac12$ degrees of freedom on a 2-dimensional spatial lattice reproduces both the infrared sector for arbitrary $\theta$, as well as the ultraviolet physics of asymptotic freedom. Furthermore, as a model of qubits on a two-dimensional square lattice with only nearest neighbor interactions, it is naturally suited for studying the physics of $\theta$ vacua and asymptotic freedom on near-term quantum devices. Our construction generalizes to $\theta$-vacua in all $\CP(N-1)$ models, solving a long standing sign problem.


