IQuS Publications
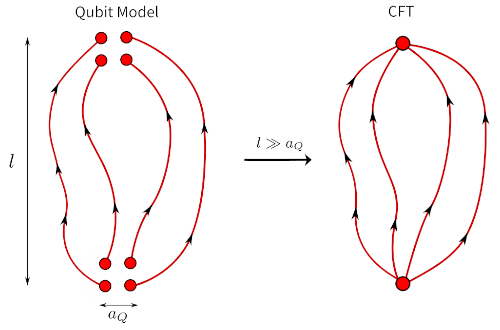
Large-charge conformal dimensions at the O(N) Wilson-Fisher fixed point
Recent work using a large-charge effective field theory (EFT) for the O(N) Wilson-Fisher conformal field theory has shown that the anomalous dimensions of large-charge operators can be expressed in terms of a few low-energy constants (LECs) of the EFT. By performing lattice Monte Carlo computations at the O(N) Wilson-Fisher critical point, we compute the anomalous dimensions of large-charge operators up to charge Q=10, and extract the leading and subleading LECs of the O(N) large-charge EFT for N=2,4,6,8. To alleviate the signal-to-noise ratio problem present in the large-charge sector of conventional lattice formulations of the O(N) theory, we employ a recently developed qubit formulation of the O(N) nonlinear sigma models with a worm algorithm. This enables us to test the validity of the large-charge expansion, and the recent predictions of large-N expansion for the coefficients of the large-charge EFT.
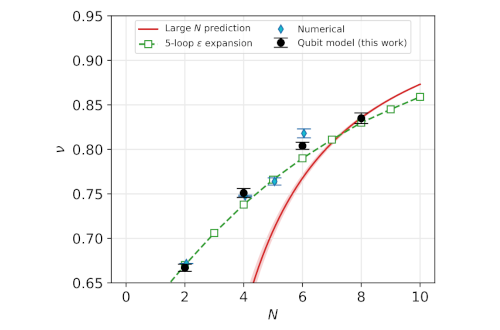
Qubit regularized O(N) nonlinear sigma models
Motivated by the prospect of quantum simulation of quantum field theories, we formulate the O(N) nonlinear sigma model as a “qubit” model with an (N+1)-dimensional local Hilbert space at each lattice site. Using an efficient worm algorithm in the worldline formulation, we demonstrate that the model has a second-order critical point in 2+1 dimensions, where the continuum physics of the nontrivial O(N) Wilson-Fisher fixed point is reproduced. We compute the critical exponents nu and eta for the O(N) qubit models up to N=8, and find excellent agreement with known results in literature from various analytic and numerical techniques for the O(N) Wilson-Fisher universality class. Our models are suited for studying O(N) nonlinear sigma models on quantum computers up to N=8 in d=2,3 spatial dimensions.
Basic Elements for Simulations of Standard Model Physics with Quantum Annealers: Multigrid and Clock States
We explore the potential of D-Wave’s quantum annealers for computing basic components required for quantum simulations of Standard Model physics. By implementing a basic multigrid (including zooming) and specializing Feynman-clock algorithms, D-Wave’s Advantage is used to study harmonic and anharmonic oscillators relevant for lattice scalar field theories and effective field theories, the time evolution of a single plaquette of SU(3) Yang-Mills lattice gauge field theory, and the dynamics of flavor entanglement in four neutrino systems.
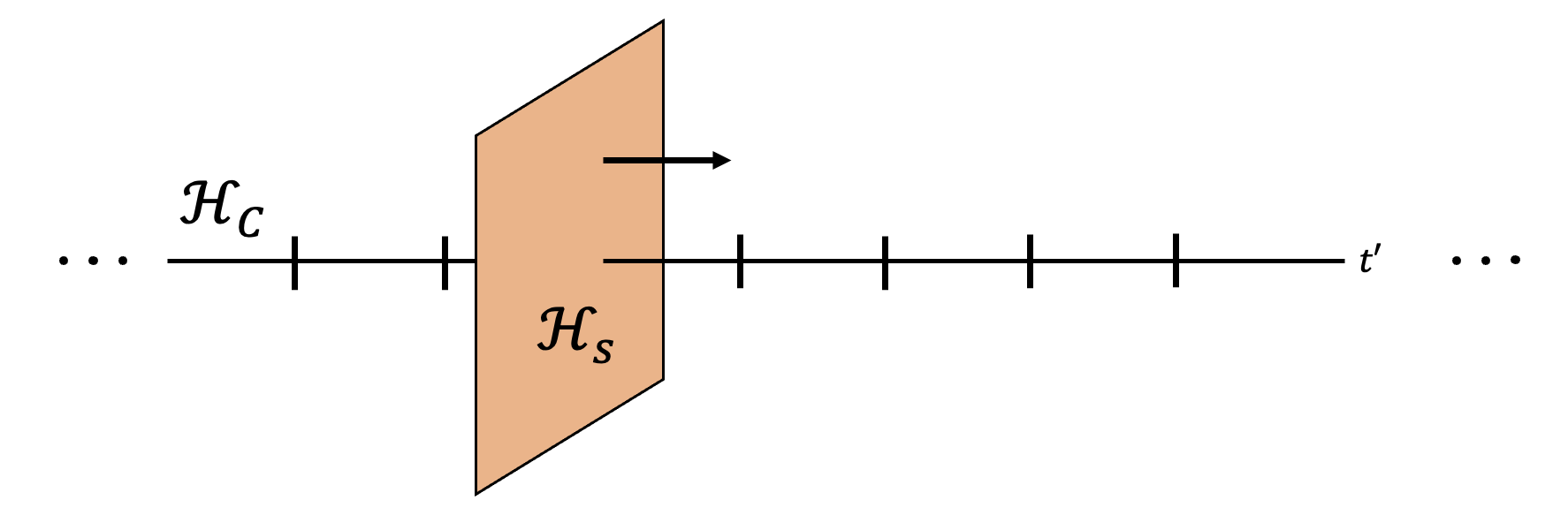
Time-dependent Hamiltonian Simulation Using Discrete Clock Constructions
In this work we provide a new approach for approximating an ordered operator exponential using
an ordinary operator exponential that acts on the Hilbert space of the simulation as well as a finite-
dimensional clock register. We show that as the number of qubits used for the clock grows, the error in
the ordered operator exponential vanishes, as well as the entanglement between the clock register and
the register of the state being acted upon. Hence, the clock is a convenient device that allows us to
translate results for simulating time-independent systems to the time-dependent case. As an application, we provide a new family of multiproduct formulas (MPFs) for time-dependent Hamiltonians that yield both commutator scaling and poly-logarithmic error scaling. This in turn, means that this method outperforms existing methods for simulating physically-local, time-dependent Hamiltonians. Finally, we apply the formalism to show how qubitization can be generalized to the time-dependent case and show that such a translation can be practical if the second derivative of the Hamiltonian is sufficiently small.

Nematic Confined Phases in the U(1) Quantum Link Model on a Triangular Lattice: An Opportunity for Near-Term Quantum Computations of String Dynamics on a Chip
The U(1) quantum link model on the triangular lattice has two rotation-symmetry-breaking nematic confined phases. Static external charges are connected by confining strings consisting of individual strands with fractionalized electric flux. The two phases are separated by a weak first order phase transition with an emergent almost exact SO(2) symmetry. We construct a quantum circuit on a chip to facilitate near-term quantum computations of the non-trivial string dynamics.
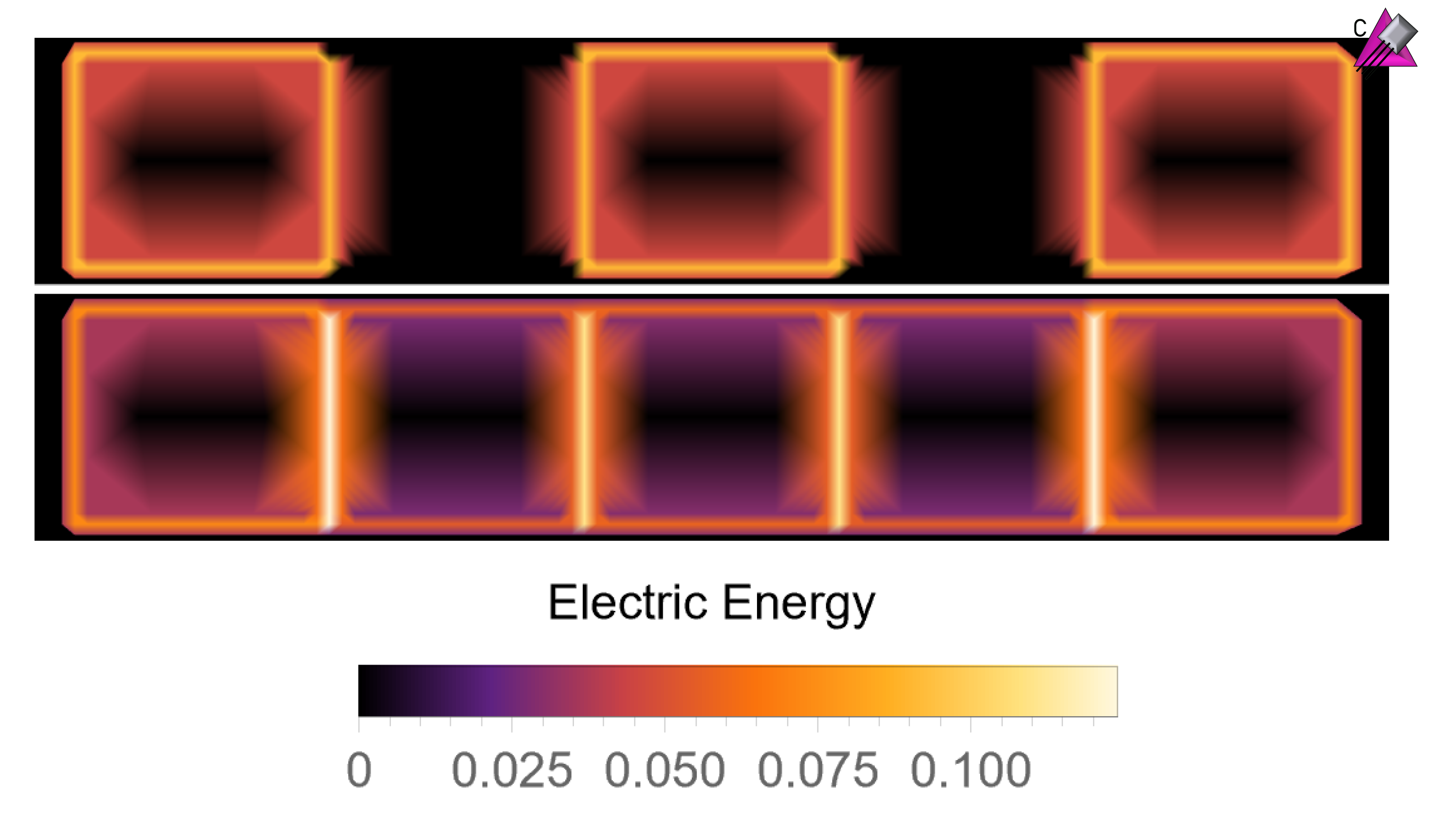
Preparation of the SU(3) Lattice Yang-Mills Vacuum with Variational Quantum Methods
Studying QCD and other gauge theories on quantum hardware requires the preparation of physically interesting states. The Variational Quantum Eigensolver (VQE) provides a way of performing vacuum state preparation on quantum hardware. In this work, VQE is applied to pure SU(3) lattice Yang-Mills on a single plaquette and one dimensional plaquette chains. Bayesian optimization and gradient descent were investigated for performing the classical optimization. Ansatz states for plaquette chains are constructed in a scalable manner from smaller systems using domain decomposition and a stitching procedure analogous to the Density Matrix Renormalization Group (DMRG). Small examples are performed on IBM’s superconducting Manila processor.
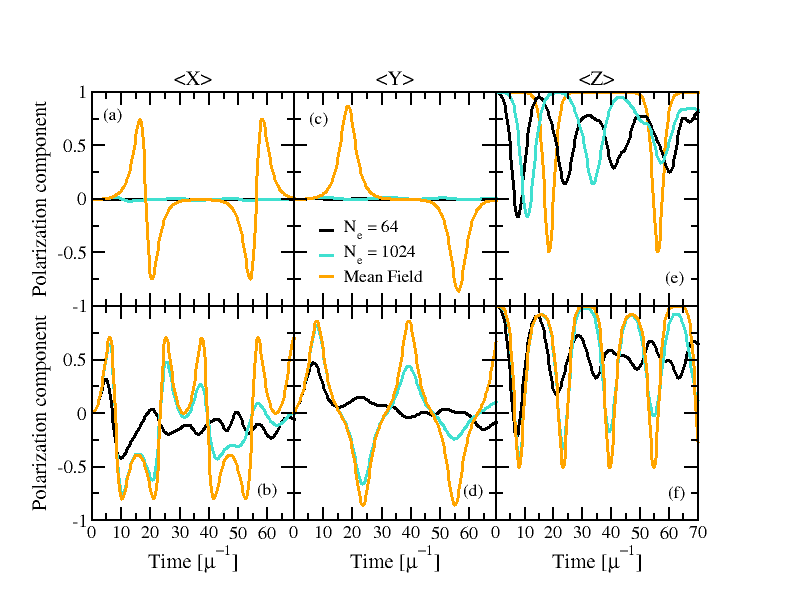
Classical and Quantum Evolution in a Simple Coherent Neutrino Problem
The extraordinary neutrino flux produced in extreme astrophysical environments like the early universe, core-collapse supernovae and neutron star mergers may produce coherent quantum neutrino oscillations on macroscopic length scales. The Hamiltonian describing this evolution can be mapped into quantum spin models with all-to-all couplings arising from neutrino-neutrino forward scattering. To date many studies of these oscillations have been performed in a mean-field limit where the neutrinos time evolve in a product state.
We examine a simple two-beam model evolving from an initial product state and compare the mean-field and many-body evolution. The symmetries in this model allow us to solve the real-time evolution for the quantum many-body system for hundreds or thousands of spins, far beyond what would be possible in a more general case with an exponential number (2N) of quantum states. We compare mean-field and many-body solutions for different initial product states and ratios of one- and two-body couplings, and find that in all cases in the limit of infinite spins the mean-field (product state) and many-body solutions coincide for simple observables. This agreement can be understood as a consequence of the spectrum of the Hamiltonian and the initial energy distribution of the product states. We explore quantum information measures like entanglement entropy and purity of the many-body solutions, finding intriguing relationships between the quantum information measures and the dynamical behavior of simple physical observables.
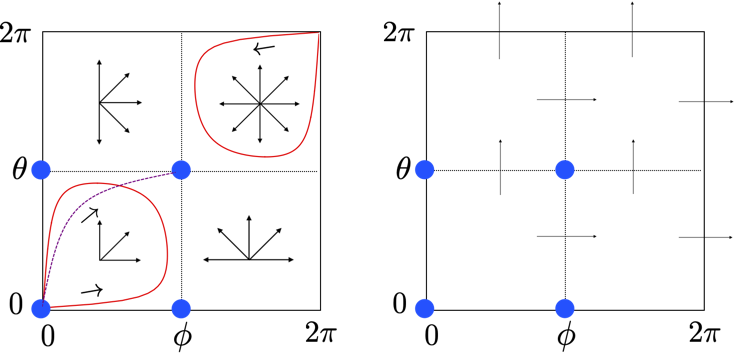
Causality and dimensionality in geometric scattering
The scattering matrix which describes low-energy,
non-relativistic scattering of two species of spin-1/2 fermions
interacting via finite-range potentials can be obtained from a
geometric action principle in which space and time do not appear
explicitly arXiv:2011.01278. In the case of zero-range
forces, constraints imposed by
causality –requiring that the scattered wave not be emitted before
the particles have interacted– translate into non-trivial
geometric constraints on scattering trajectories in the geometric
picture. The dependence of scattering on the number of spatial dimensions
is also considered; by varying from three to two spatial dimensions, the
dependence on spatial dimensionality in the geometric picture is
found to be encoded in the phase of the harmonic potential that appears in
the geometric action.

UV/IR symmetries of the S-matrix and RG flow
The low energy S-matrix which describes non-relativistic two-body
scattering arising from finite-range forces has UV/IR symmetries
that are hidden in the corresponding effective field theory (EFT) action.
It is shown that the S-matrix symmetries are manifest as geometric properties
of the RG flow of the coefficients of local operators in the EFT action.
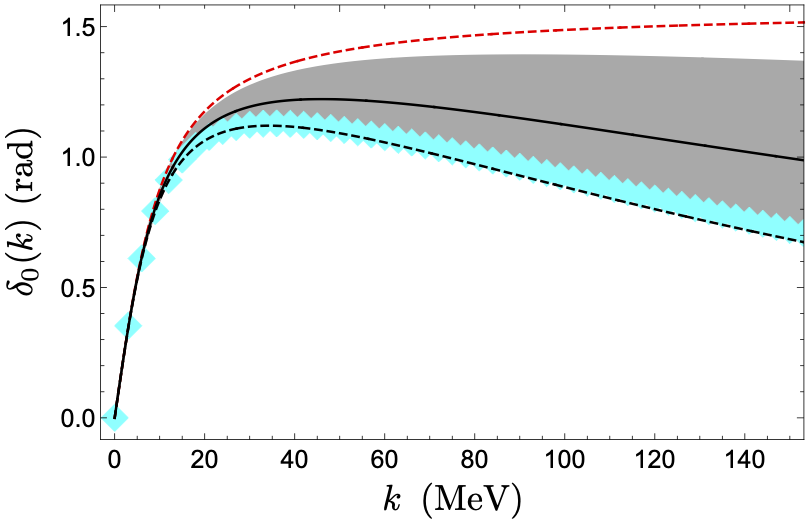
Symmetries of the nucleon-nucleon S-matrix and effective field theory expansions
The s-wave nucleon-nucleon (NN) scattering matrix
(S-matrix) exhibits UV/IR symmetries which are hidden in the
effective field theory (EFT) action and scattering amplitudes, and
which explain some interesting generic features of the phase
shifts. These symmetries offer clarifying interpretations of
existing pionless EFT expansions, and suggest starting points for
novel expansions. The leading-order (LO) S-matrix obtained in the
pionless EFT with scattering lengths treated exactly is shown to
have a UV/IR symmetry which leaves the sum of s-wave phase shifts
invariant. A new scheme, which treats effective range corrections
exactly, and which possesses a distinct UV/IR symmetry at LO, is
developed up to NLO (next-to-LO) and compared with data.


