IQuS Publications

UV/IR symmetries of the S-matrix and RG flow
The low energy S-matrix which describes non-relativistic two-body
scattering arising from finite-range forces has UV/IR symmetries
that are hidden in the corresponding effective field theory (EFT) action.
It is shown that the S-matrix symmetries are manifest as geometric properties
of the RG flow of the coefficients of local operators in the EFT action.
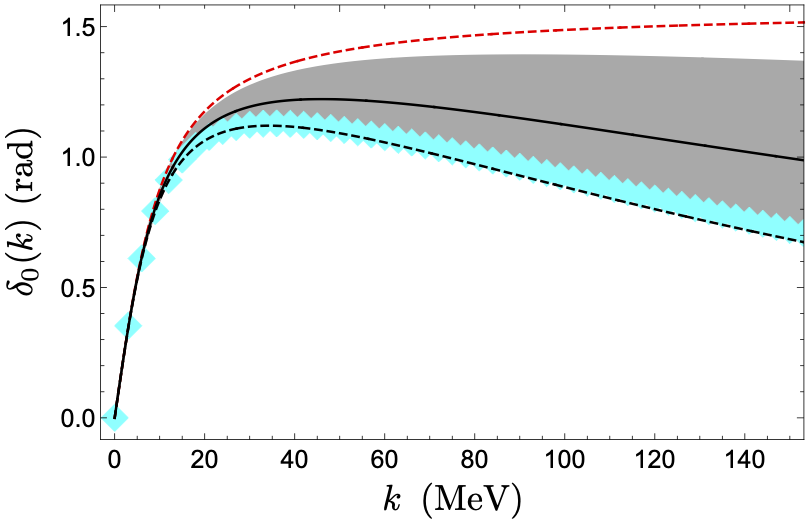
Symmetries of the nucleon-nucleon S-matrix and effective field theory expansions
The s-wave nucleon-nucleon (NN) scattering matrix
(S-matrix) exhibits UV/IR symmetries which are hidden in the
effective field theory (EFT) action and scattering amplitudes, and
which explain some interesting generic features of the phase
shifts. These symmetries offer clarifying interpretations of
existing pionless EFT expansions, and suggest starting points for
novel expansions. The leading-order (LO) S-matrix obtained in the
pionless EFT with scattering lengths treated exactly is shown to
have a UV/IR symmetry which leaves the sum of s-wave phase shifts
invariant. A new scheme, which treats effective range corrections
exactly, and which possesses a distinct UV/IR symmetry at LO, is
developed up to NLO (next-to-LO) and compared with data.
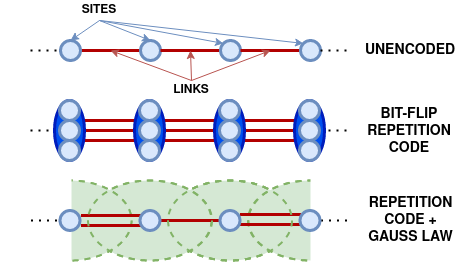
Quantum Error Correction with Gauge Symmetries
Quantum simulations of Lattice Gauge Theories (LGTs) are often formulated on an enlarged Hilbert space containing both physical and unphysical sectors in order to retain a local Hamiltonian. We provide simple fault-tolerant procedures that exploit such redundancy by combining a phase flip error correction code with the Gauss’ law constraint to correct one-qubit errors for a Z2 or truncated U(1) LGT in 1+1 dimensions with a link flux cutoff of 1. Unlike existing work on detecting violations of Gauss’ law, our circuits are fault tolerant and the overall error correction scheme outperforms a naive application of the [5,1,3] code. The constructions outlined can be extended to LGT systems with larger cutoffs and may be of use in understanding how to hybridize error correction and quantum simulation for LGTs in higher space-time dimensions and with different symmetry groups.
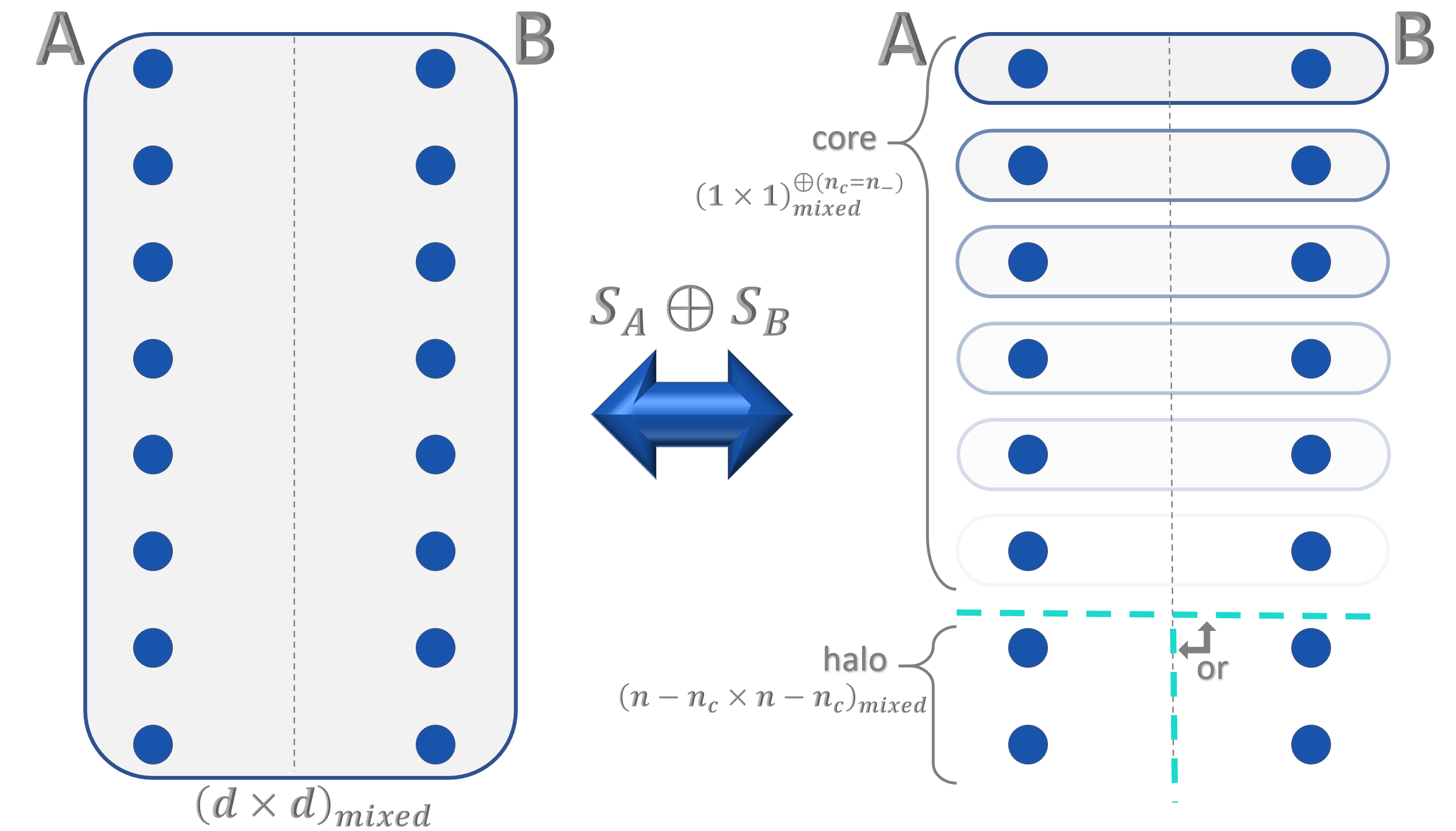
Entanglement Structures in Quantum Field Theories: Negativity Cores and Bound Entanglement in the Vacuum
The many-body entanglement between two finite (size-d) disjoint vacuum regions of noninteracting lattice scalar field theory in one spatial dimension, i.e., a (dA×dB)mixed Gaussian continuous variable system, is locally transformed into a tensor-product core of (1A×1B)mixed entangled pairs. Accessible entanglement within these core pairs exhibits an exponential hierarchy and as such identifies the structure of dominant region modes from which vacuum entanglement could be extracted into a spatially separated pair of quantum detectors. Beyond the core, the remaining modes of the halo are determined to be AB separable in isolation, as well as separable from the core. However, state preparation protocols that distribute entanglement in the form of (1A×1B)mixed core pairs are found to require additional entanglement in the halo that is obscured by classical correlations. This inaccessible (bound) halo entanglement is found to mirror the accessible entanglement, but with a step behavior as the continuum is approached. It remains possible that alternate initialization protocols that do not utilize the exponential hierarchy of core-pair entanglement may require less inaccessible entanglement. Entanglement consolidation is expected to persist in higher dimensions and may aid classical and quantum simulations of asymptotically free gauge field theories, such as quantum chromodynamics.
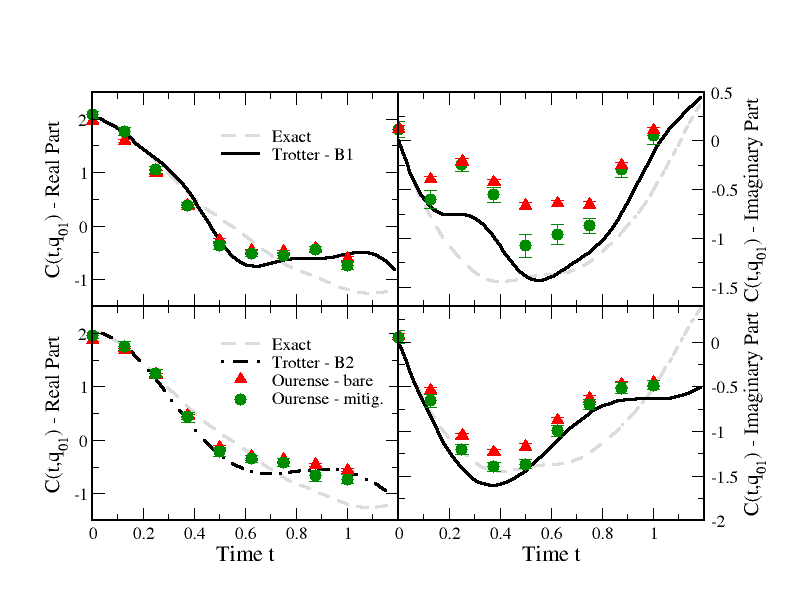
Nuclear two point correlation functions on a quantum computer
The calculation of dynamic response functions are expected to be an early application benefiting from rapidly developing quantum hardware resources. The ability to calculate real-time quantities of strongly-correlated quantum systems is one of the most exciting applications that can easily reach beyond the capabilities of traditional classical hardware. Response functions of fermionic systems at moderate momenta and energies corresponding roughly to the Fermi energy of the system are a potential early application because the relevant operators are nearly local and the energies can be resolved in moderately short real time, reducing the spatial resolution and gate depth required.
This is particularly the case in quasielastic electron and neutrino scattering from nuclei, a topic of great interest in the nuclear and particle physics communities and directly related to experiments designed to probe neutrino properties. In this work we use current hardware to calculate response functions for a highly simplified nuclear model through calculations of a 2-point real time correlation function for a Fermi-Hubbard model in two dimensions with three distinguishable nucleons on four lattice sites on current quantum hardware, and evaluate current error mitigation strategies.
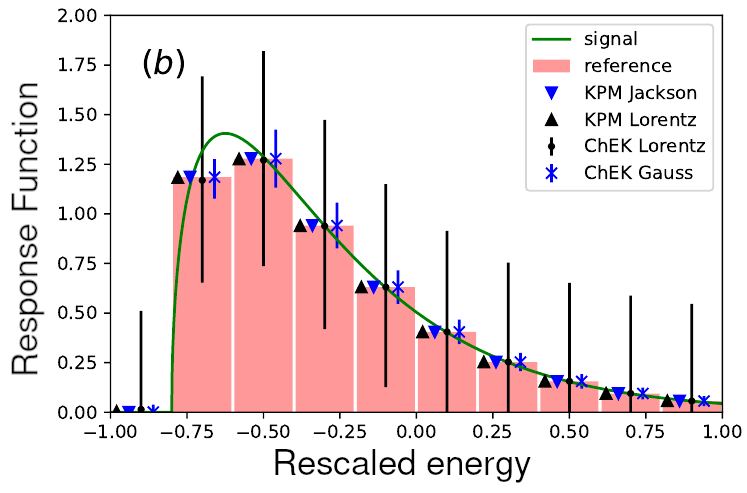
Spectral density reconstruction with Chebyshev polynomials
Accurate calculations of the spectral density in a strongly correlated quantum many body system are of fundamental importance to study many-particle dynamics in the linear response regime. Typical examples are the calculation of inclusive and semi-exclusive scattering cross sections in atomic nuclei and transport properties of nuclear and neutron star matter. Integral transform techniques have played an important role in accessing the spectral density in a variety of nuclear systems. However, their accuracy is in practice limited by the need to perform a numerical inversion which is often ill-conditioned.
In order to circumvent this problem, a quantum algorithm based on an appropriate expansion in Chebyshev polynomials was recently proposed. In the present work we build on this idea. We show how to perform controllable reconstructions of the spectral density over a finite energy resolution with rigorous error estimates while allowing for efficient simulations on classical computers. We apply our idea to simple model response functions and comment on the applicability of the method to study realistic systems using scalable nuclear many-body methods.
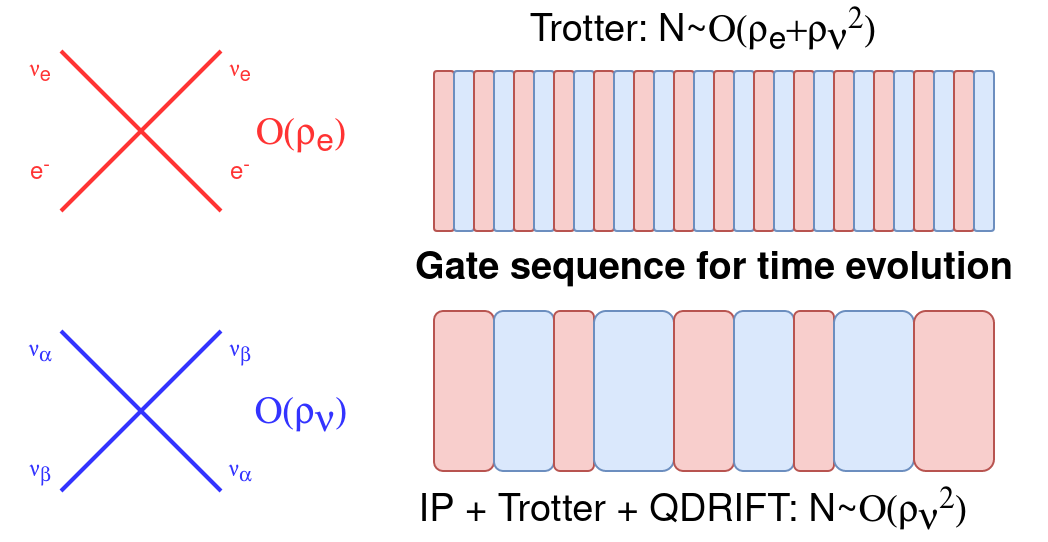
Hybridized Methods for Quantum Simulation in the Interaction Picture
Conventional methods of quantum simulation involve trade-offs that limit their applicability to specific contexts where their use is optimal. This paper demonstrates how different simulation methods can be hybridized to improve performance for interaction picture simulations over known algorithms. These approaches show asymptotic improvements over the individual methods that comprise them and further make interaction picture simulation methods practical in the near term. Physical applications of these hybridized methods yields a gate complexity scaling as log²Λ in the electric cutoff Λ for the Schwinger Model and independent of the electron density for collective neutrino oscillations, outperforming the scaling for all current algorithms with these parameters. For the general problem of Hamiltonian simulation subject to dynamical constraints, these methods yield a query complexity independent of the penalty parameter λ used to impose an energy cost on time-evolution into an unphysical subspace.
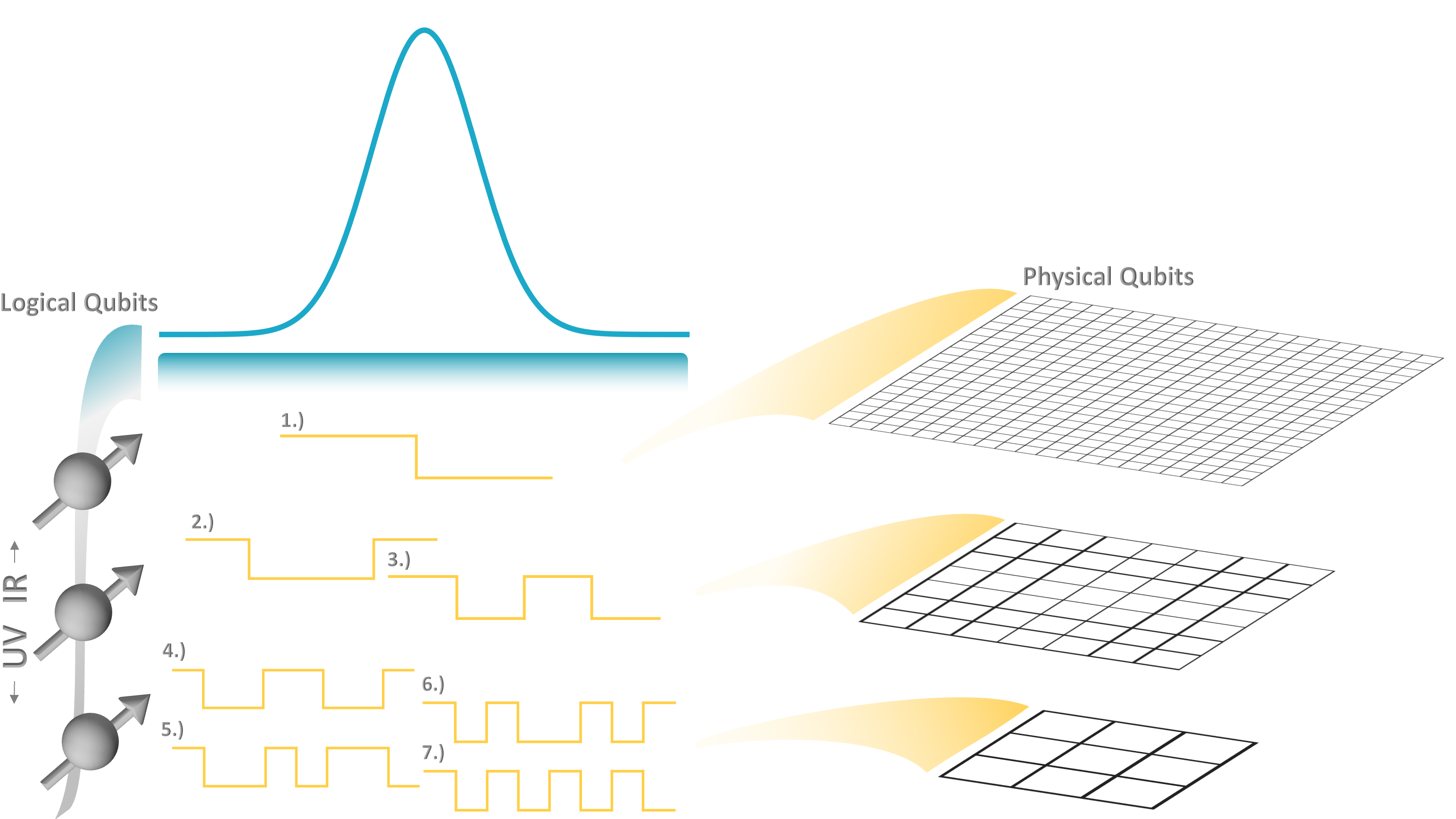
Hierarchical Qubit Maps and Hierarchical Quantum Error Correction
We consider hierarchically implemented quantum error correction (HI-QEC) in which the fidelities of logical qubits are differentially optimized to enhance the capabilities of quantum devices in scientific applications. By employing qubit representations that propagate hierarchies in simulated systems to those in logical qubit noise sensitivities, heterogeneity in the distribution of physical qubits among logical qubits can be systematically structured. For concreteness, we estimate HI-QEC’s impact on surface code resources in computing low-energy observables to a fixed precision, finding up to ~60% reductions in qubit requirements possible in early error corrected simulations. This heterogeneous distribution of physical-to-logical qubits is identified as another element that can be optimized in the co-design process of quantum simulations of Standard Model physics.
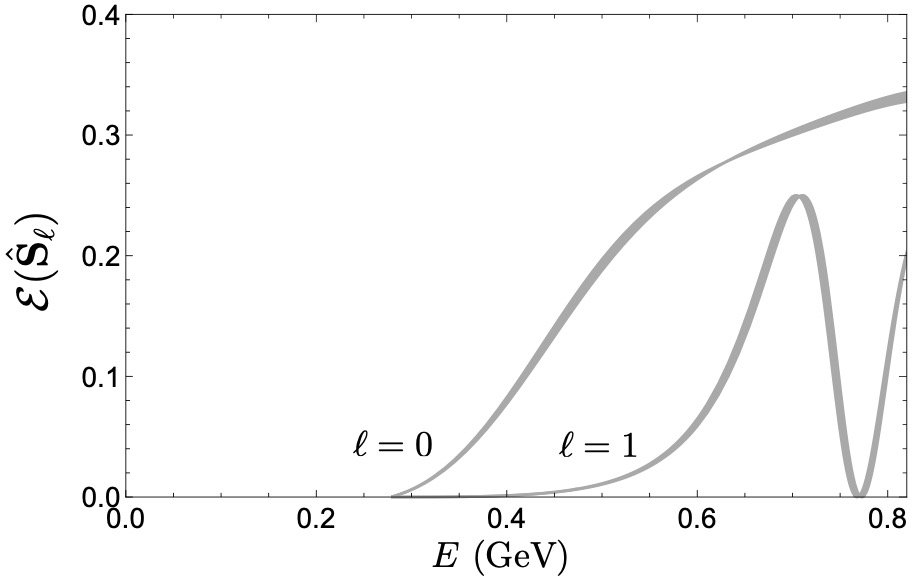
Entanglement minimization in hadronic scattering with pions
Recent work conjectured that
entanglement is minimized in low-energy hadronic scattering
processes. It was shown that the minimization of the entanglement
power (EP) of the low-energy baryon-baryon S-matrix implies novel
spin-flavor symmetries that are distinct from large-N_c QCD
predictions and are confirmed by high-precision lattice QCD
simulations. Here the conjecture of minimal entanglement is
investigated for scattering processes involving pions and
nucleons. The EP of the S-matrix is constructed for the pi-pi
and pi-N systems, and the consequences of minimization of
entanglement are discussed and compared with large-N_c QCD
expectations.
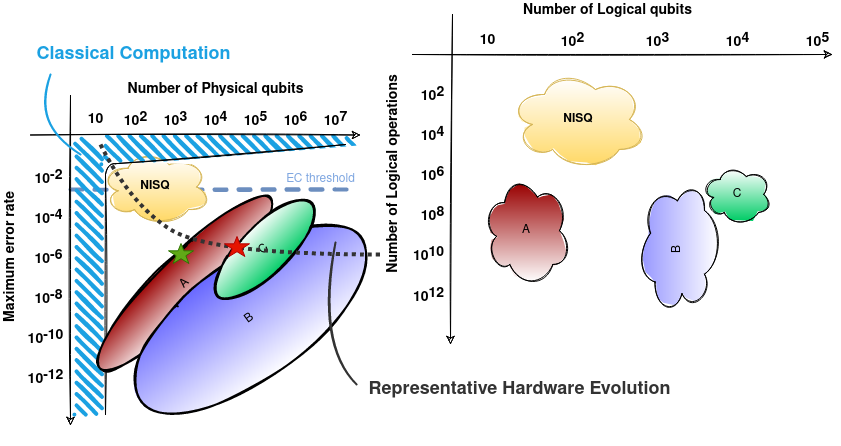
Standard Model Physics and the Digital Quantum Revolution: Thoughts about the Interface
Remarkable advances in isolating, controlling and entangling quantum systems are transforming what was once a curious feature of quantum mechanics into a vehicle for disruptive scientific and technological progress. Pursuing the vision articulated by Feynman, a concerted effort across many areas of research and development is introducing prototypical digital quantum devices into the computing ecosystem available to domain scientists. Through interactions with these early quantum devices, the abstract vision of exploring classically-intractable quantum systems is evolving toward becoming a tangible reality. Beyond catalyzing these technological advances, entanglement is enabling parallel progress as a diagnostic for quantum correlations and as an organizational tool, both guiding improved understanding of quantum many-body systems and quantum field theories defining and emerging from the Standard Model. From the perspective of three domain science theorists, this article compiles “thoughts about the interface” on entanglement, complexity, and quantum simulation in an effort to contextualize recent NISQ-era progress with the scientific objectives of nuclear and high-energy physics.


