IQuS Publications
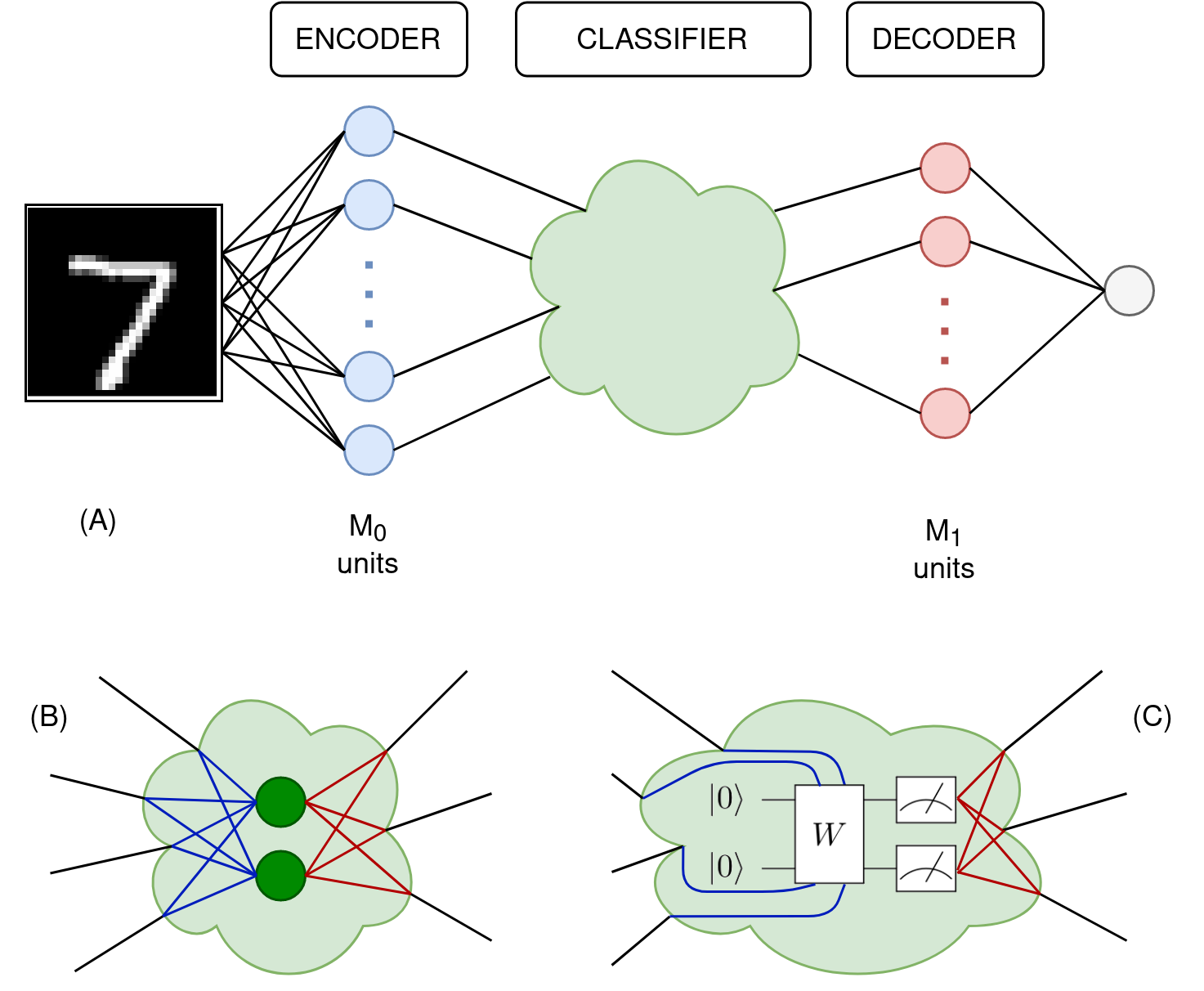
Quantum Machine Learning with SQUID
In this work we present the Scaled QUantum IDentifier (SQUID), an open-source framework for exploring hybrid Quantum-Classical algorithms for classification problems. The classical infrastructure is based on PyTorch and we provide a standardized design to implement a variety of quantum models with the capability of back-propagation for efficient training. We present the structure of our framework and provide examples of using SQUID in a standard binary classification problem from the popular MNIST dataset. In particular we highlight the implications for scalability for gradient based optimization of quantum models on the choice of output for variational quantum models.
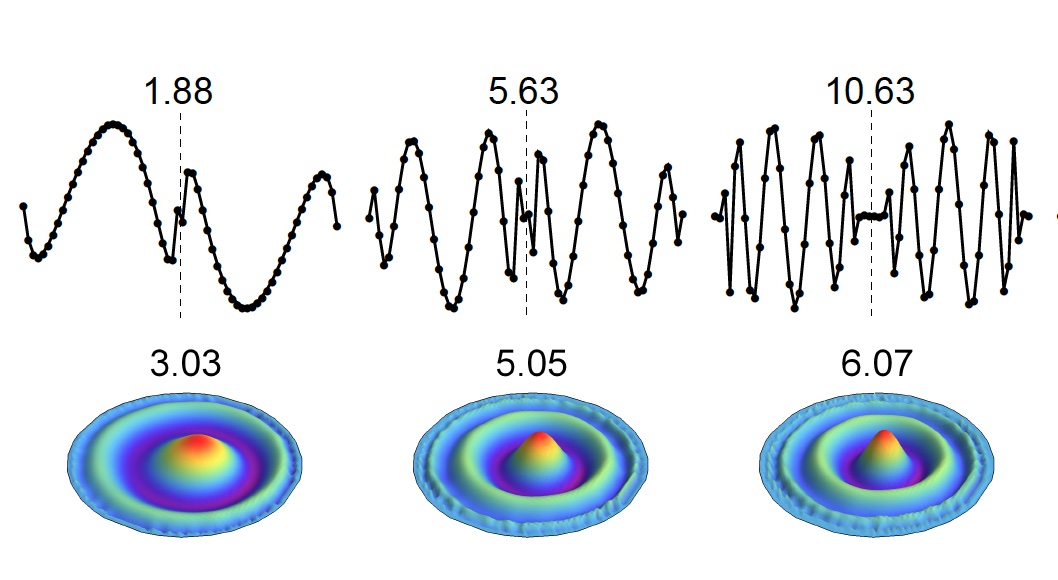
Entanglement Spheres and a UV-IR connection in Effective Field Theories
Disjoint regions of the latticized, massless scalar field vacuum become separable at large distances beyond the entanglement sphere, a distance that extends to infinity in the continuum limit. Through numerical calculations in one-, two- and three-dimensions, the radius of an entanglement sphere is found to be determined by the highest momentum mode of the field supported across the diameter, d, of two identical regions. As a result, the long-distance behavior of the entanglement is determined by the short-distance structure of the field. Effective eld theories (EFTs), describing a system up to a given momentum scale Lambda, are expected to share this feature, with regions of the EFT vacuum separable (or dependent on the UV-completion) beyond a distance proportional to Λ. The smallest non-zero value of the entanglement negativity supported by the field at large distances is conjectured to be NN~exp(-Λ d), independent of the number of spatial dimensions. This phenomenon may be manifest in perturbative QCD processes.
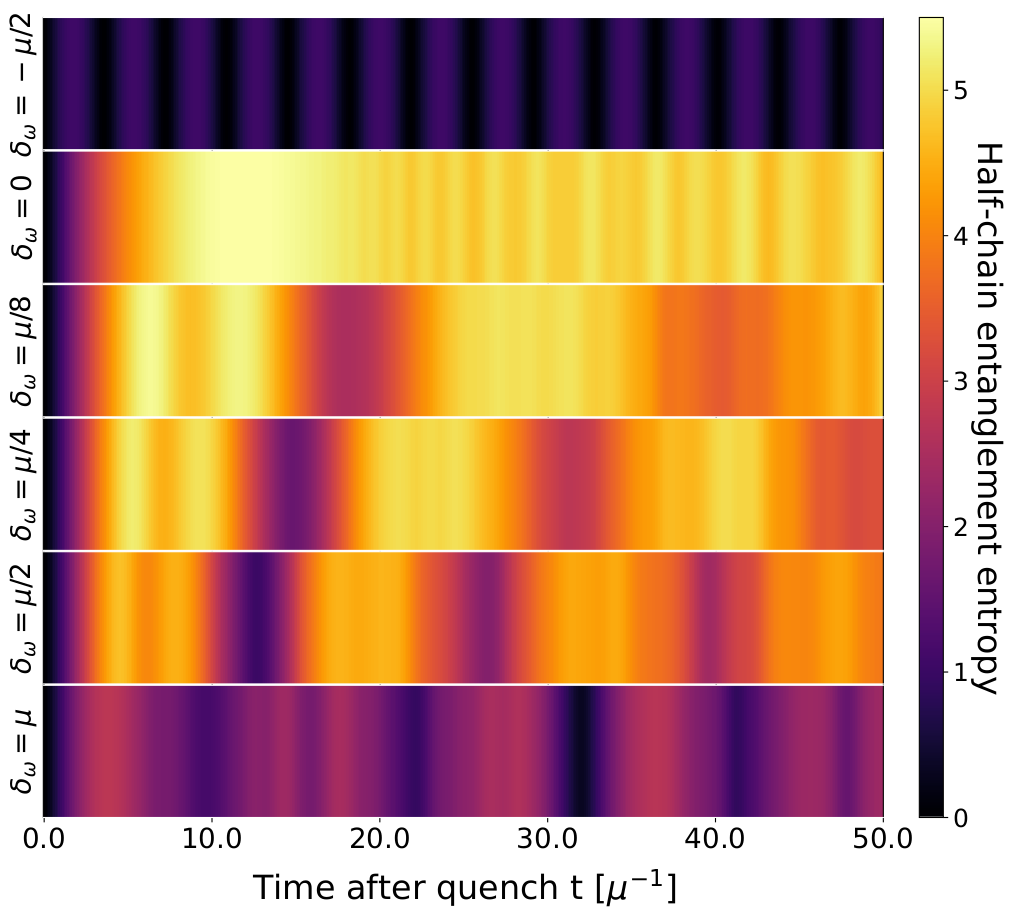
Dynamical Phase Transitions in models of Collective Neutrino Oscillations
Collective neutrino oscillations can potentially play an important role in transporting lepton flavor in astrophysical scenarios where the neutrino density is large, typical examples are the early universe and supernova explosions. It has been argued in the past that simple models of the neutrino Hamiltonian designed to describe forward scattering can support substantial flavor evolution on very short time scales t≈log(N)/(GFρ), with N the number of neutrinos, GF the Fermi constant and ρ the neutrino density. This finding is in tension with results for a similar but exactly solvable model for which t≈√N/(GFρ) instead. In this work we provide a coherent explanation of this tension in terms of Dynamical Phase Transitions (DPT) and study the possible impact that a DPT could have in more realistic models of neutrino oscillations and their mean-field approximation.
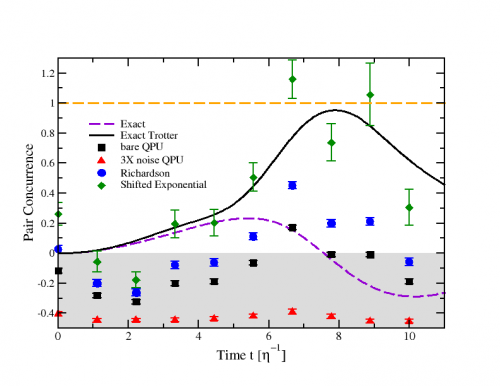
Simulation of Collective Neutrino Oscillations on a Quantum Computer
In astrophysical scenarios with large neutrino density, like supernovae and the early universe, the presence of neutrino-neutrino interactions can give rise to collective flavor oscillations in the out-of-equilibrium collective dynamics of a neutrino cloud. The role of quantum correlations in these phenomena is not yet well understood, in large part due to complications in solving for the real-time evolution of the strongly coupled many-body system. Future fault-tolerant quantum computers hold the promise to overcome much of these limitations and provide direct access to the correlated neutrino dynamic. In this work, we present the first simulation of a small system of interacting neutrinos using current generation quantum devices. We introduce a strategy to overcome limitations in the natural connectivity of the qubits and use it to track the evolution of entanglement in real-time. The results show the critical importance of error-mitigation techniques to extract meaningful results for entanglement measures using noisy, near term, quantum devices.
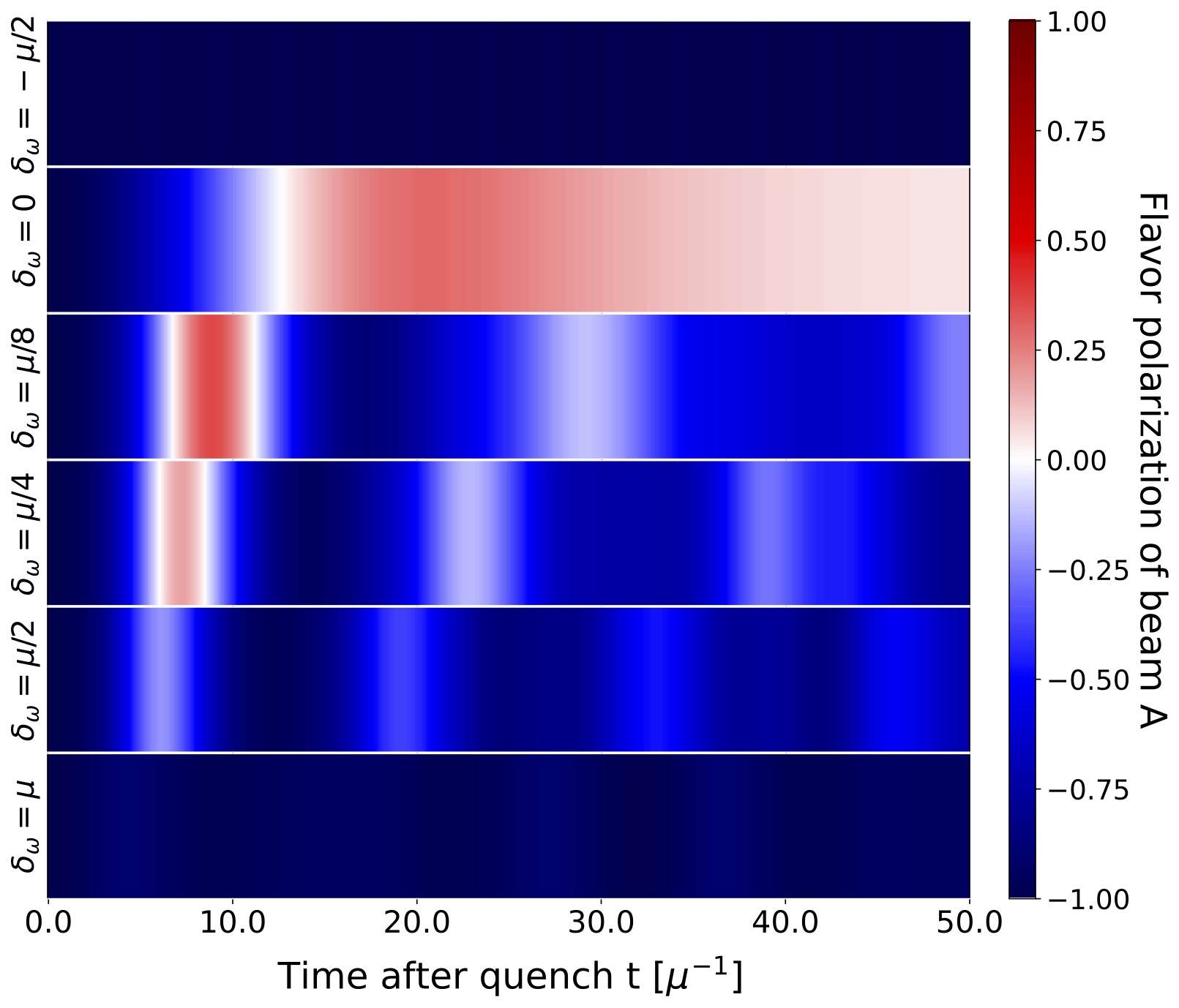
Entanglement and Many-Body Effects in Collective Neutrino Oscillations
Collective neutrino oscillations play a crucial role in transporting lepton flavor in astrophysical settings, such as supernovae, where the neutrino density is large. In this regime, neutrino-neutrino interactions are important and simulations in mean-field approximations show evidence for collective oscillations occurring at time scales much larger than those associated with vacuum oscillations. In this work, we study the out-of-equilibrium dynamics of a corresponding spin model using Matrix Product States and show how collective bipolar oscillations can be triggered by quantum fluctuations if appropriate initial conditions are present. The origin of these flavor oscillations, absent in the mean-field, can be traced to the presence of a dynamical phase transition, which drastically modifies the real-time evolution of the entanglement entropy. We find entanglement entropies scaling at most logarithmically in the system size, suggesting that classical tensor network methods could be efficient in describing collective neutrino dynamics more generally.
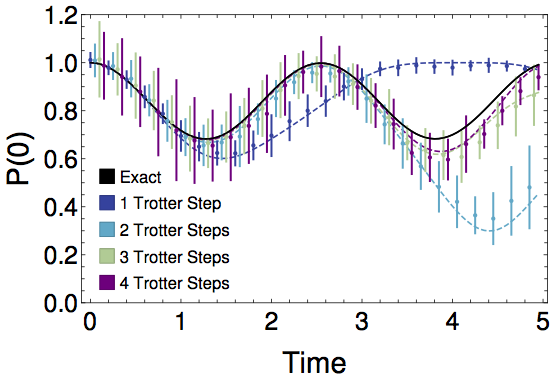
A Trailhead for Quantum Simulation of SU(3) Yang-Mills Lattice Gauge Theory in the Local Multiplet Basis
Maintaining local interactions in the quantum simulation of gauge field theories relegates most states in the Hilbert space to be unphysical—theoretically benign, but experimentally difficult to avoid. Reformulations of the gauge fields can modify the ratio of physical to gauge-variant states often through classically preprocessing the Hilbert space and modifying the representation of the field on qubit degrees of freedom. This paper considers the implications of representing SU(3) Yang-Mills gauge theory on a lattice of irreducible representations in both a global basis of projected global quantum numbers and a local basis in which controlled-plaquette operators support efficient time evolution. Classically integrating over the internal gauge space at each vertex (e.g., color isospin and color hypercharge) significantly reduces both the qubit requirements and the dimensionality of the unphysical Hilbert space. Initiating tuning procedures that may inform future calculations at scale, the time evolution of one- and two-plaquettes are implemented on one of IBM’s superconducting quantum devices, and early benchmark quantities are identified. The potential advantages of qudit environments, with either constrained 2D hexagonal or 1D nearest-neighbor internal state connectivity, are discussed for future large-scale calculations.
Editors Suggestion in Physical Review D.
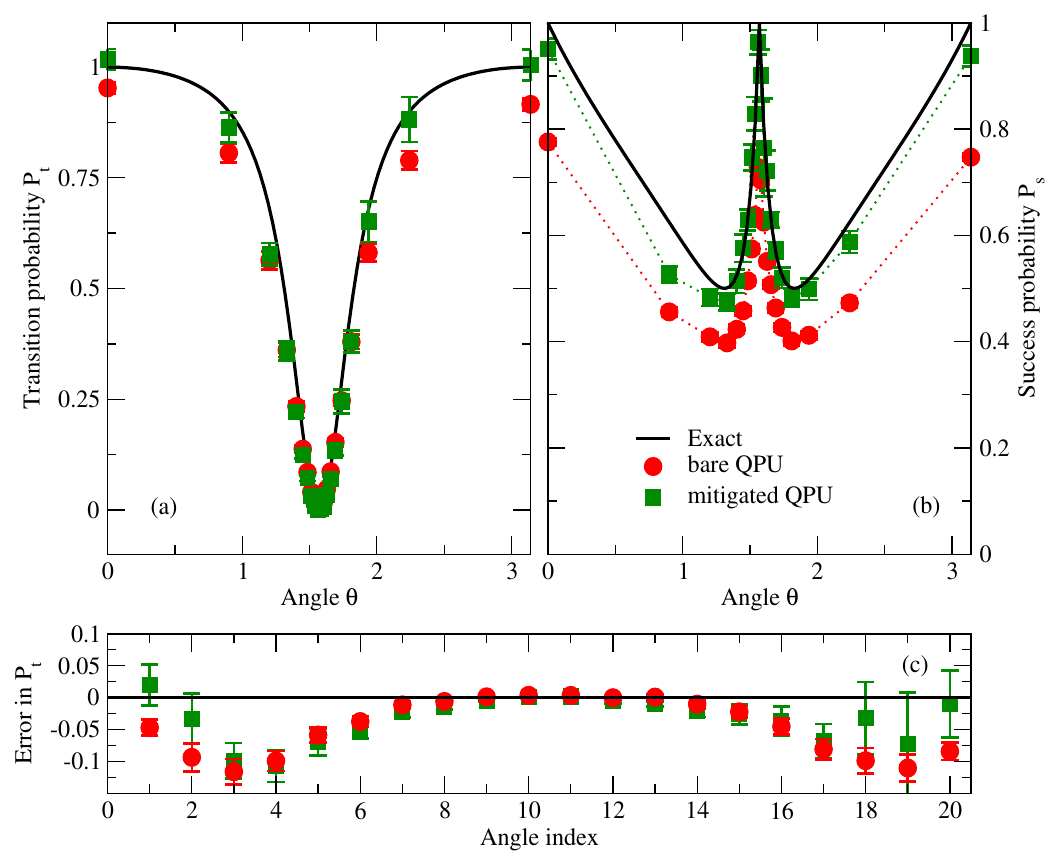
Preparation of Excited States for Nuclear Dynamics on a Quantum Computer
We study two different methods to prepare excited states on a quantum computer, a key initial step to study dynamics within linear response theory. The first method uses unitary evolution for a short timeT=O(√(1−F)) to approximate the action of an excitation operator O with fidelity Fand success probability P≈1−F. The second method probabilistically applies the excitation operator using the Linear Combination of Unitaries (LCU) algorithm. We benchmark these techniques on emulated and real quantum devices, using a toy model for thermal neutron-proton capture. Despite its larger memory footprint, the LCU-based method is efficient even on current generation noisy devices and can be implemented at a lower gate cost than a naive analysis would suggest. These findings show that quantum techniques designed to achieve good asymptotic scaling on fault tolerant quantum devices might also provide practical benefits on devices with limited connectivity and gate fidelity.
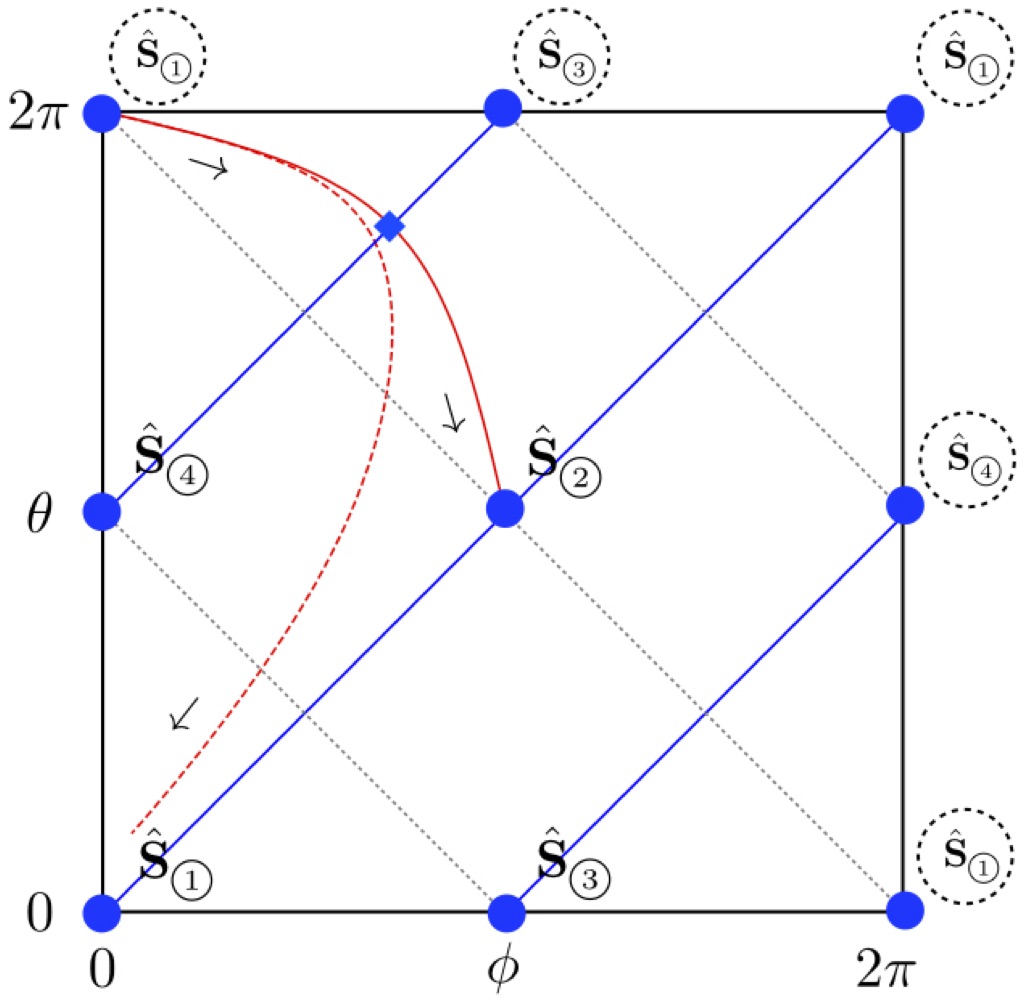
Geometry and entanglement in the scattering matrix
A formulation of nucleon-nucleon scattering is developed in which the S-matrix, rather than an effective-field theory (EFT) action, is the fundamental object. Spacetime plays no role in this description: the S-matrix is a trajectory that moves between RG fixed points in a compact theory space defined by unitarity. This theory space has a natural operator definition, and a geometric embedding of the unitarity constraints in four-dimensional Euclidean space yields a flat torus, which serves as the stage on which the S-matrix propagates. Trajectories with vanishing entanglement are special geodesics between RG fixed points on the flat torus, while entanglement is driven by an external potential. The system of equations describing S-matrix trajectories is in general complicated, however the very-low-energy S-matrix — that appears at leading-order in the EFT description — possesses a UV/IR conformal invariance which renders the system of equations integrable, and completely determines the potential. In this geometric viewpoint, inelasticity is in correspondence with the radius of a three-dimensional hyperbolic space whose two-dimensional boundary is the flat torus. This space has a singularity at vanishing radius, corresponding to maximal violation of unitarity. The trajectory on the flat torus boundary can be explicitly constructed from a bulk trajectory with a quantifiable error, providing a simple example of a holographic quantum error correcting code.
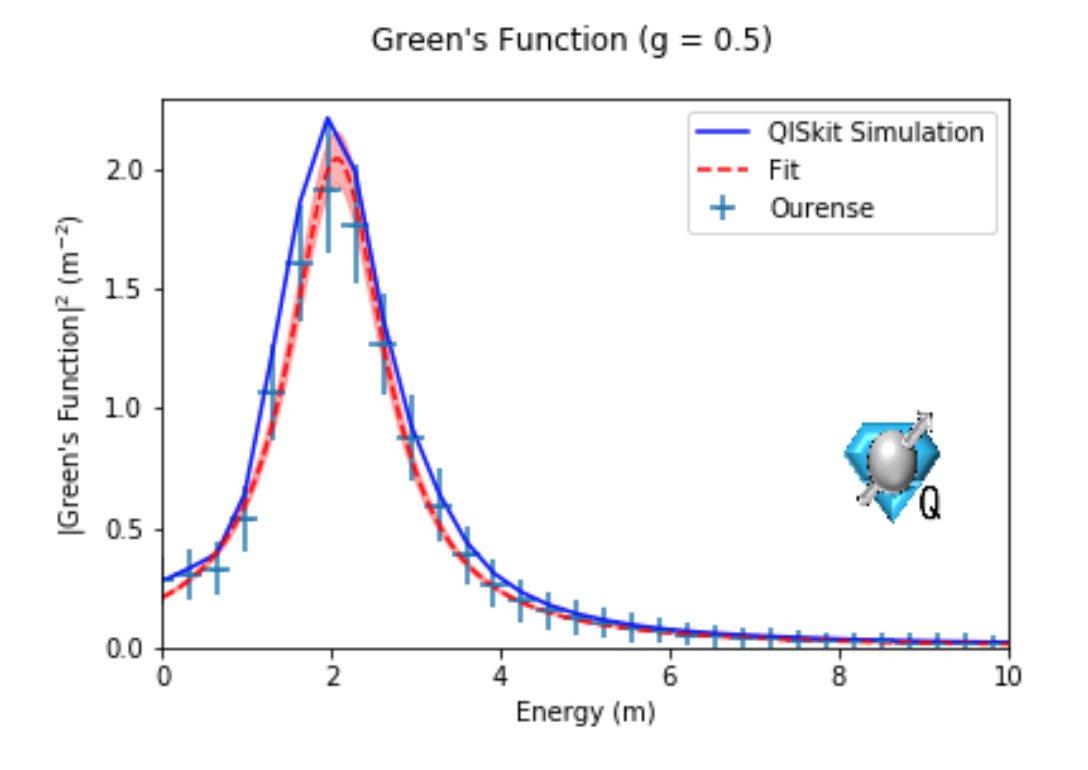
An Algorithm for Quantum Computation of Particle Decays
A quantum algorithm is developed to calculate decay rates and cross sections using quantum resources that scale polynomially in the system size assuming similar scaling for state preparation and time evolution. This is done by computing finite-volume one- and two-particle Green’s functions on the quantum hardware. Particle decay rates and two particle scattering cross sections are extracted from the imaginary parts of the Green’s function. A 0 + 1 dimensional implementation of this method is demonstrated on IBM’s superconducting quantum hardware for the decay of a heavy scalar particle to a pair of light scalars.
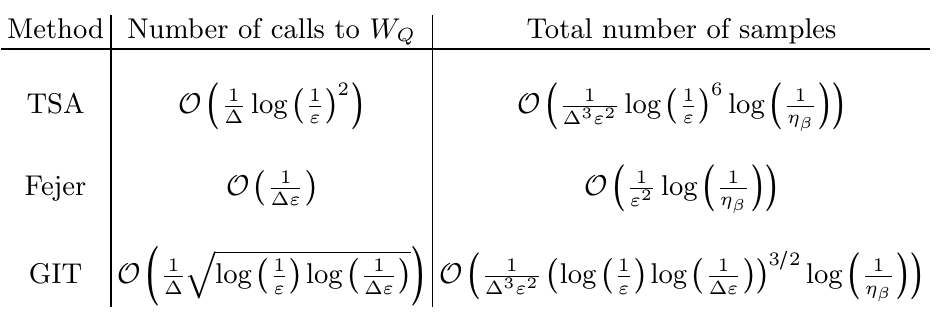
Spectral Density Estimation with the Gaussian Integral Transform
The spectral density operator ρ(ω)=δ(ω−H) plays a central role in linear response theory as it’s expectation value, the dynamical response function, can be used to compute scattering cross-sections. In this work, we describe a near optimal quantum algorithm providing an approximation to the spectral density with energy resolution Δ and error ϵ using O(√(log(1/ϵ)(log(1/Δ)+log(1/ϵ)))/Δ) operations. This is achieved without using expensive approximations to the time-evolution operator but exploiting instead qubitization to implement an approximate Gaussian Integral Transform (GIT) of the spectral density. We also describe appropriate error metrics to assess the quality of spectral function approximations more generally.


