IQuS Publications
Universal corrections to the superfluid gap in a cold Fermi gas
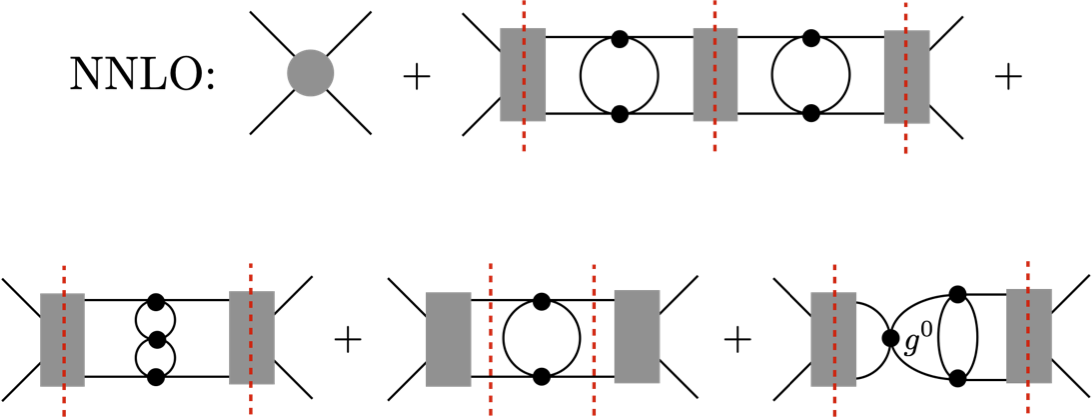
A framework for computing the superfluid gap in an effective field theory (EFT) of fermions interacting via momentum independent contact forces is developed. The leading universal corrections in the EFT are one-loop in-medium effects at the Fermi surface, and reproduce the well-known Gor’kov-Melik-Barkhudarov result. The complete subleading universal corrections are presented here, and include one-loop effects away from the Fermi surface, two-loop in-medium effects, as well as modifications to the fermion propagator. Together, these effects are found to reduce the gap at low densities. Applications to neutron superfluidity in neutron stars are discussed.
This work was supported by the Swiss National Science Foundation (SNSF) under grant numbers 200021_192137 and PCEFP2_203335, by the U. S. Department of Energy grant DE-FG02-97ER-41014 (UW Nuclear Theory) and by the U. S. Department of Energy grant DE-SC0020970, (InQubator for Quantum Simulation).
Qutrit and Qubit Circuits for Three-Flavor Collective Neutrino Oscillations
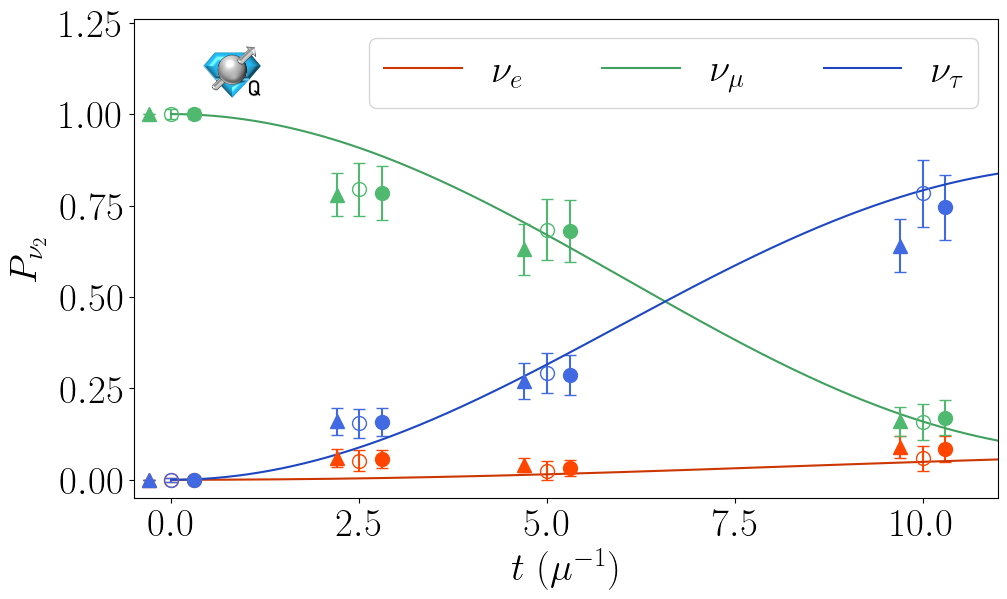
We explore the utility of qutrits and qubits for simulating the flavor dynamics of dense neutrino systems. The evolution of such systems impacts some important astrophysical processes, such as core-collapse supernovae and the nucleosynthesis of heavy nuclei. Many-body simulations require classical resources beyond current computing capabilities for physically relevant system sizes. Quantum computers are therefore a promising candidate to efficiently simulate the many-body dynamics of collective neutrino oscillations. Previous quantum simulation efforts have primarily focused on properties of the two-flavor approximation due to their direct mapping to qubits. Here, we present new quantum circuits for simulating three-flavor neutrino systems on qutrit- and qubit-based platforms, and demonstrate their feasibility by simulating systems of two, four and eight neutrinos on IBM and Quantinuum quantum computers.
This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS)9 under DOE (NP) Award No. DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Turro, Bhaskar, Chernyshev), and the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (DOE) (Illa). This work is also supported, in part, through the Department of Physics12 and the College of Arts and Sciences at the University of Washington. This research used resources of the Oak Ridge Leadership Computing Facility (OLCF), which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725. We acknowledge the use of IBM Quantum services for this work.
Entanglement Structure of Non-Gaussian States and How to Measure It
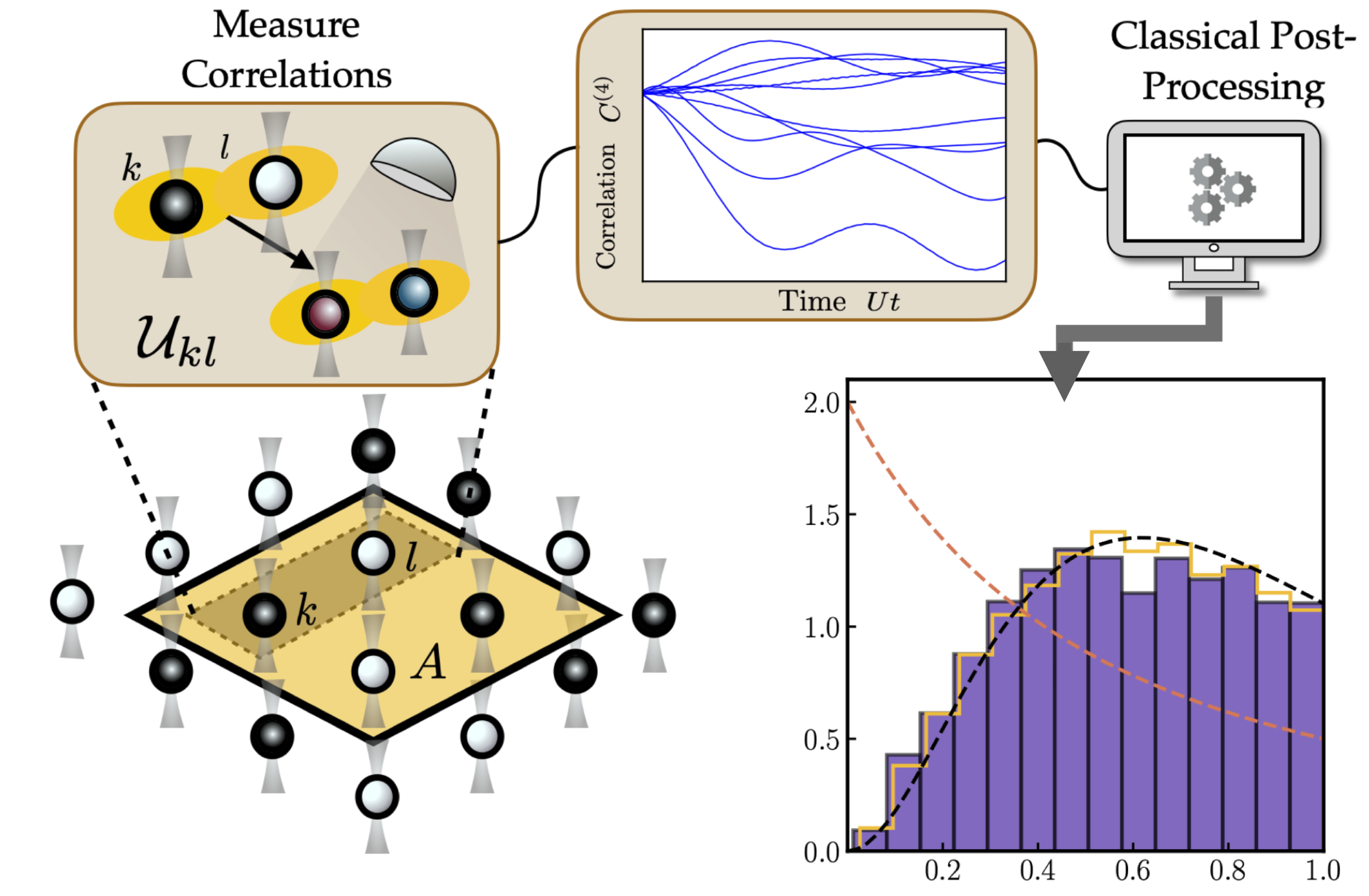
Rapidly growing capabilities of quantum simulators to probe quantum many-body phenomena require new methods to characterize increasingly complex states. We present a protocol that constrains quantum states by experimentally measured correlation functions which only scales polynomially with system size. This method enables measurement of a quantum state’s entanglement structure, opening a new route to study entanglement-related phenomena. Our approach extends Gaussian state parameterizations by systematically incorporating higher-order correlations. We show the protocol’s usefulness in conjunction with current and forthcoming experimental capabilities, focusing on weakly interacting fermions as a proof of concept. Here, the lowest non-trivial expansion quantitatively predicts early time thermalization dynamics, including signaling the on-set of quantum chaos indicated by the entanglement Hamiltonian.
This work is supported by the DOE, Office of Science, Office of Nuclear Physics, IQuS (\url{https://iqus.uw.edu}), via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science under Award DE-SC0020970 and by the European Union’s Horizon Europe research and innovation program under Grant Agreement No. 101113690 (PASQuanS2.1), the ERC Starting grant QARA (Grant No.~101041435), the EU-QUANTERA project TNiSQ (N-6001), and by the Austrian Science Fund (FWF): COE 1 and quantA. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington
Evaluation of phase shifts for non-relativistic elastic scattering using quantum computers
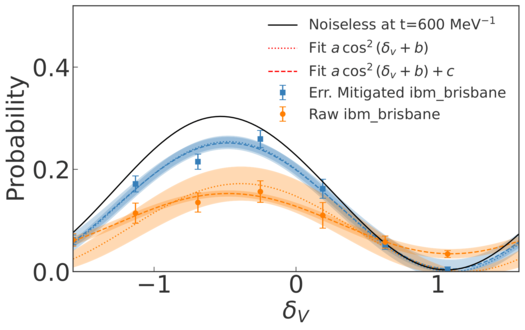
Simulations of scattering processes are essential in understanding the physics of our universe. Computing relevant scattering quantities from ab initio methods is extremely difficult on classical devices because of the substantial computational resources needed. This work reports the development of an algorithm that makes it possible to obtain phase shifts for generic non-relativistic elastic scattering processes on a quantum computer. Such algorithm is based on extracting phase shifts from the direct implementation of the real-time evolution. The algorithm is improved by a variational procedure, making it more accurate and resistant to the noise of quantum . The reliability of the algorithm is first demonstrated by means of classical numerical simulations for different potentials, and later tested on existing quantum hardware, specifically on IBM quantum processors.
This work was supported in part by the U.S. De- partment of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quan- tum Horizons: QIS Research and Innovation for Nuclear Science. This work was prepared in part by LLNL under Contract No. DE- AC52-07NA27344 with sup- port from the U.S. Department of Energy, Office of Sci- ence, Office of Nuclear Physics (under Work Proposal No. SCW1730). This work was enabled by the use of advanced compu- tational, storage, and networking infrastructure provided by the Hyak supercomputer system at the University of Washington (https://hyak.uw.edu/).
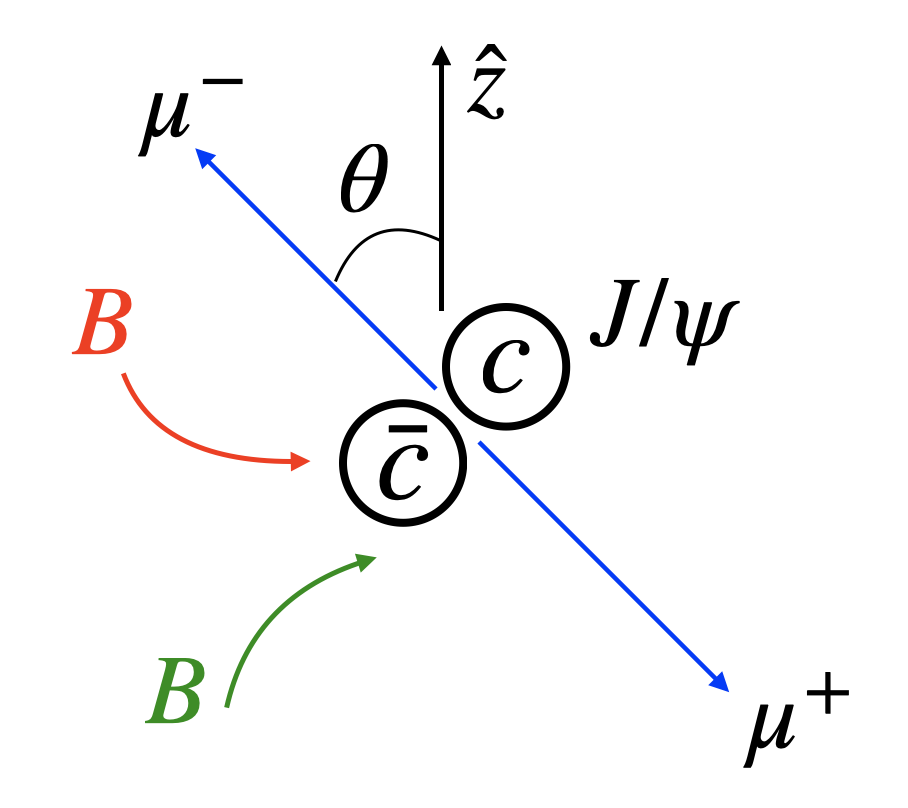
Quarkonium Polarization in Medium from Open Quantum Systems and Chromomagnetic Correlators
We study the spin-dependent in-medium dynamics of quarkonia by using the potential nonrelativistic QCD (pNRQCD) and the open quantum system framework. We consider the pNRQCD Lagrangian valid up to the order. r/M^0=r and r^0/M=1/M in the double power counting. By considering the Markovian condition and applying the Wigner transformation upon the diagonal spin components of the quarkonium density matrix with the semiclassical expansion, we systematically derive the Boltzmann transport equation for quarkonia with polarization dependence in the quantum optical limit. Unlike the spin-independent collision terms governed by certain chromoelectric field correlators, new gauge invariant correlators of chromomagnetic fields determine the recombination and dissociation terms with polarization dependence at the order we are working. We also derive a Lindblad equation describing the in-medium transitions between spin-singlet and spin-triplet heavy quark-antiquark pairs in the quantum Brownian motion limit. The Lindblad equation is governed by new transport coefficients defined in terms of the chromomagnetic field correlators. Our formalism is generic and valid for both weakly-coupled and strongly-coupled quark gluon plasmas. It can be further applied to study spin alignment of vector quarkonia in heavy ion collisions.
This work was supported in part by National Science and Technology Council (Taiwan) under Grant No. MOST 110-2112-M-001-070-MY, by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science.
Three-flavor Collective Neutrino Oscillations on D-Wave’s Advantage Quantum Annealer
In extreme environments such as core-collapse supernovae, neutron-star mergers, and the early Universe, neutrinos are dense enough that their self-interactions significantly affect, if not dominate, their flavor dynamics. In order to develop techniques for characterizing the resulting quantum entanglement, I present the results of simulations of Dirac neutrino-neutrino interactions that include all three physical neutrino flavors and were performed on D-Wave Inc.’s Advantage 5000+ qubit annealer. These results are checked against those from exact classical simulations, which are also used to compare the Dirac neutrino-neutrino interactions to neutrino-antineutrino and Majorana neutrino-neutrino interactions. The D-Wave Advantage annealer is shown to be able to reproduce time evolution with the precision of a classical machine for small numbers of neutrinos and to do so without Trotter errors. However, it suffers from poor scaling in qubit-count with the number of neutrinos. Two approaches to improving the qubit-scaling are discussed, but only one of the two shows promise.
This work was supported in part by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) [154] under Award Number DOE (NP) Award DE- SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science and by the Quantum Computing Summer School 2023 at Los Alamos National Laboratory (LANL).
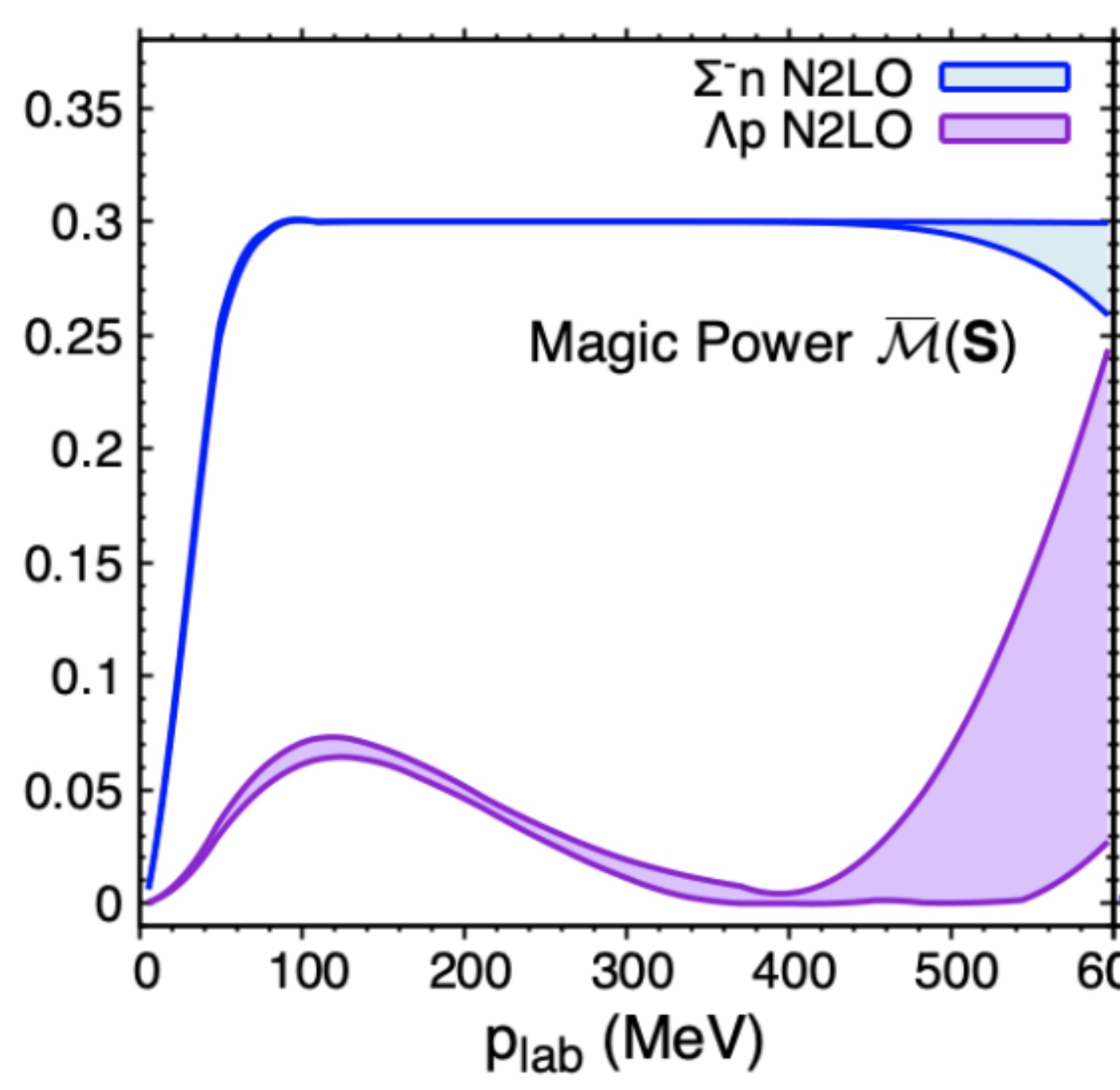
The Magic in Nuclear and Hypernuclear Forces
Toward an improved understanding of the role of quantum information in nuclei and exotic matter, we examine the magic (non-stabilizerness) in low-energy strong interaction processes. As stabilizer states can be prepared efficiently using classical computers, and include classes of entangled states, it is magic and fluctuations in magic, along with entanglement, that determine resource requirements for quantum simulations. As a measure of fluctuations in magic induced by scattering, the “magic power” of the S-matrix is introduced. Using experimentally determined scattering phase shifts and mixing parameters, the magic power in nucleon-nucleon and hyperon-nucleon scattering, along with the magic in the deuteron, are found to exhibit interesting features. The Sigma-minus baryon is identified as a potential candidate catalyst for enhanced spreading of magic and entanglement in dense matter, depending on in-medium decoherence.
This work was supported, in part, by Universität Bielefeld and ERC- 885281-KILONOVA Advanced Grant (Caroline), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science4 (Martin). This work was supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.
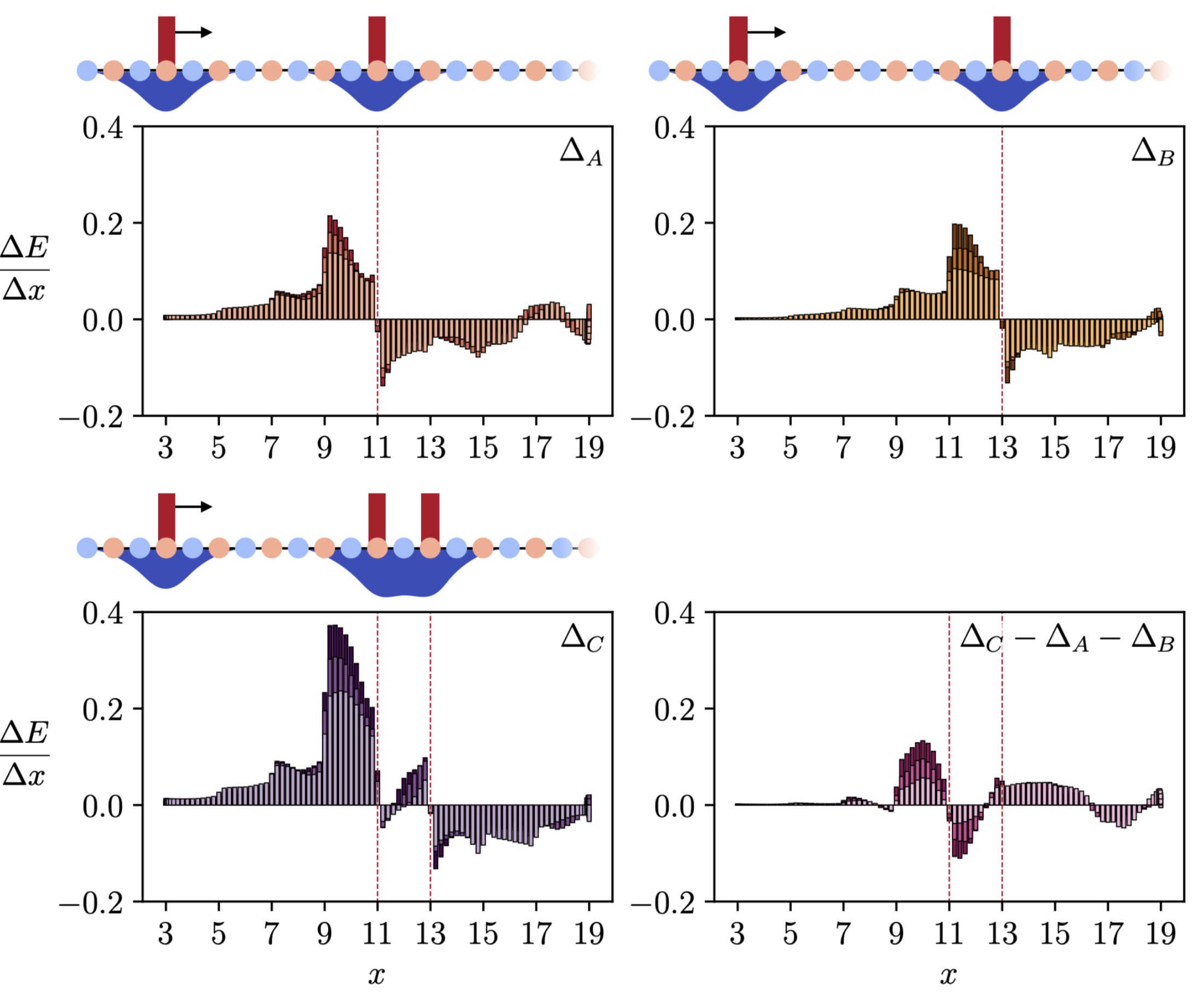
Steps Toward Quantum Simulations of Hadronization and Energy-Loss in Dense Matter
A framework for simulating the real-time dynamics of particles in dense matter using quantum computers is developed. This formalism is used to simulate heavy-hadrons propagating through a dense medium in the Schwinger model. Measurements of the time-dependent energy and charge density are used to identify mechanisms responsible for energy loss and hadron production (hadronization). A study of entanglement dynamics highlights the importance of quantum coherence between the particles that make up the dense medium. Throughout this work, care is taken to isolate, and remove, phenomena that arise solely from a finite lattice spacing. An efficient method and the corresponding quantum circuits for preparing ground states in the presence of heavy mesons are presented. These circuits are used to estimate the resources required to simulate in-medium energy loss and hadronization in the Schwinger model using quantum computers.
This work was supported, in part, by the U.S. Department of Energy grant DE-FG02-97ER-41014 (Roland), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Roland, Martin), the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (DOE) (Marc). This work is also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.
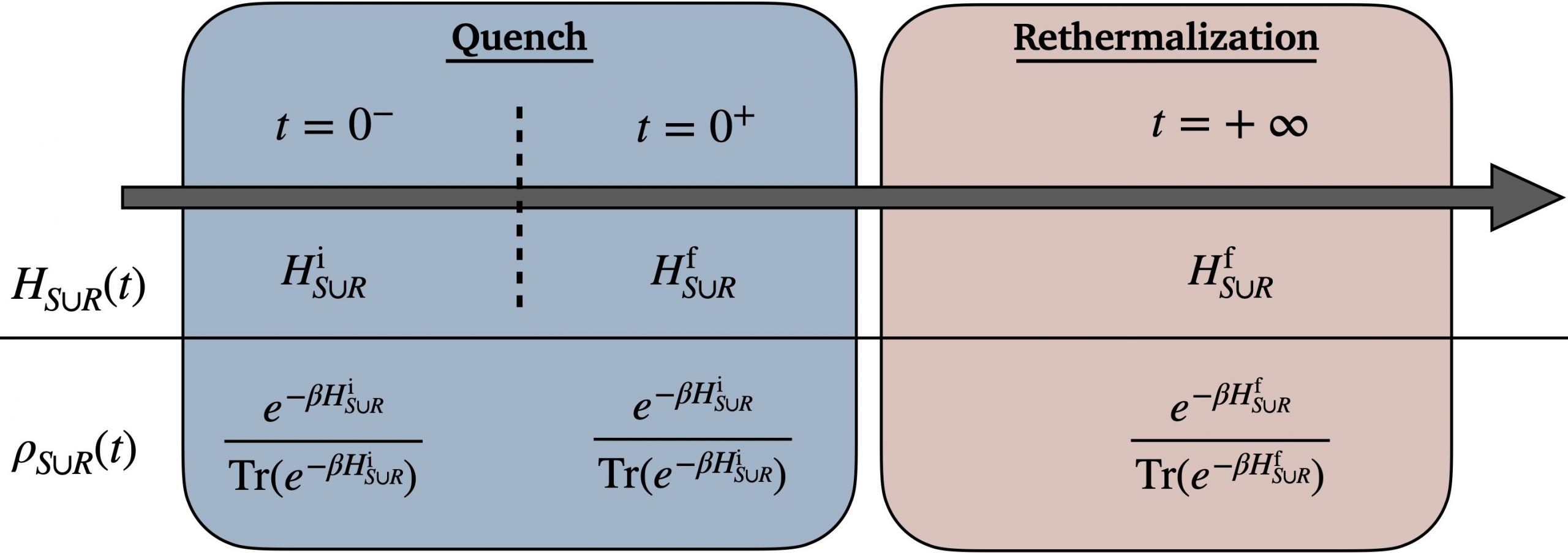
Quantum thermodynamics of nonequilibrium processes in lattice gauge theories
A key objective in nuclear and high-energy physics is to describe nonequilibrium dynamics of matter, e.g., in the early universe and in particle colliders, starting from the Standard Model. Classical-computing methods, via the framework of lattice gauge theory, have experienced limited success in this mission. Quantum simulation of lattice gauge theories holds promise for overcoming computational limitations. Because of local constraints (Gauss’s laws), lattice gauge theories have an intricate Hilbert-space structure. This structure complicates the definition of thermodynamic properties of systems coupled to reservoirs during equilibrium and nonequilibrium processes. We show how to define thermodynamic quantities such as work and heat using strong-coupling thermodynamics, a framework that has recently burgeoned within the field of quantum thermodynamics. Our definitions suit instantaneous quenches, simple nonequilibrium processes undertaken in quantum simulators. To illustrate our framework, we compute the work and heat exchanged during a quench in a $Z_2$ lattice gauge theory coupled to matter in 1+1 dimensions. The thermodynamic quantities, as functions of the quench parameter, evidence an expected phase transition. Generally, we derive a simple relation between a quantum many-body system’s entanglement Hamiltonian, measurable with quantum-information-processing tools, and the Hamiltonian of mean force, used to define strong-coupling thermodynamic quantities.
This work was supported in part by the National Science Foundation (NSF) Quantum Leap Challenge Institutes (QLCI) (award no. OMA-2120757), by the Department of Energy (DOE), Office of Science, Early Career Award (award no. DESC0020271), and by the Department of Physics, Maryland Center for Fundamental Physics, and the College of Computer, Mathematical, and Natural Sciences at the University of Maryland, College Park, and the Simons Foundation through the Simons Foundation Emmy Noether Fellows Program at Perimeter Institute, by the John Templeton Foundation (award no. 62422), and by the DOE, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (award no. DE-SC0020970).
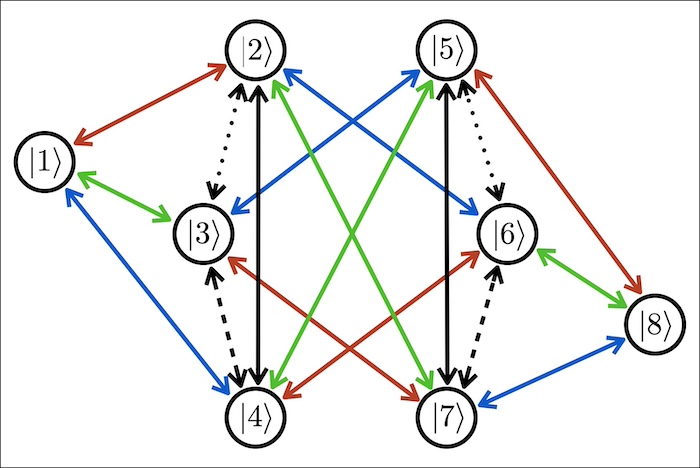
Qu8its for Quantum Simulations of Lattice Quantum Chromodynamics
We explore the utility of d=8 qudits, qu8its, for quantum simulations of the dynamics of 1+1D SU(3) lattice quantum chromodynamics, including a mapping for arbitrary numbers of flavors and lattice size and a re-organization of the Hamiltonian for efficient time-evolution. Recent advances in parallel gate applications, along with the shorter application times of single-qudit operations compared with two-qudit operations, lead to significant projected advantages in quantum simulation fidelities and circuit depths using qu8its rather than qubits. The number of two-qudit entangling gates required for time evolution using qu8its is found to be more than a factor of five fewer than for qubits. We anticipate that the developments presented in this work will enable improved quantum simulations to be performed using emerging quantum hardware.
This work was supported, in part, by Universität Bielefeld and ERC-885281-KILONOVA Advanced Grant (Caroline Robin), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, Inqubator for Quantum Simulation (IQuS)9 under Award Number DOE (NP) Award DE-SC0020970 (Martin Savage), and the Quantum Science Center (QSC), a National Quantum Information Science Research Center of the U.S. Department of Energy (Marc Illa). This work was supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.


