IQuS Publications
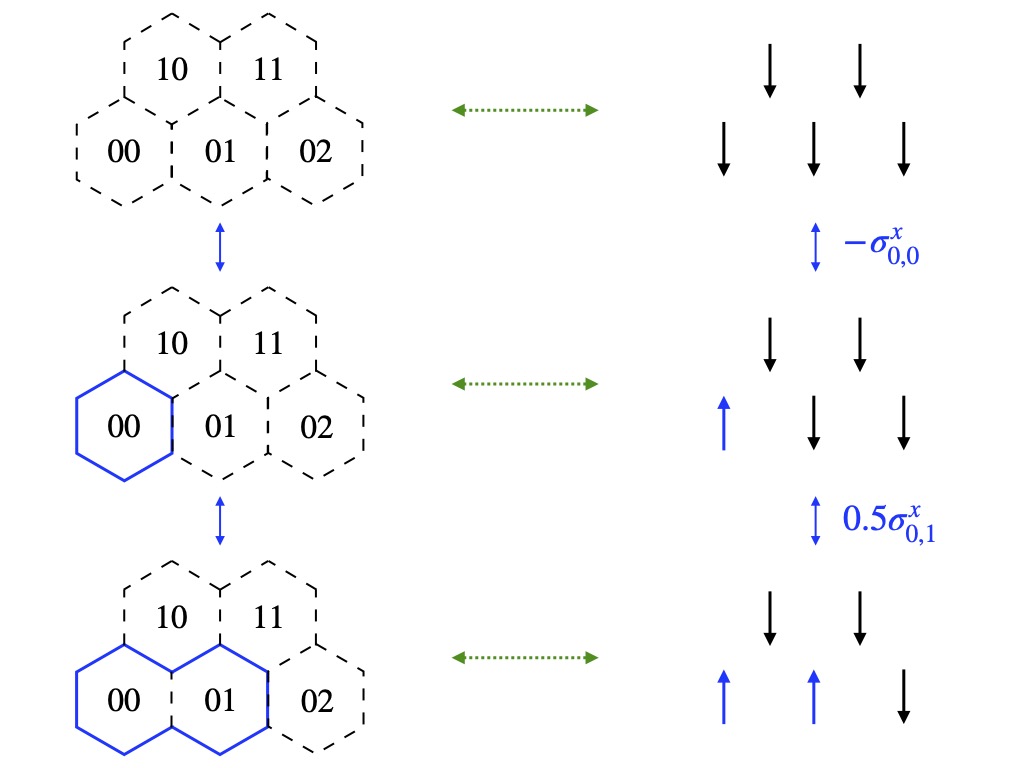
Simple Hamiltonian for Quantum Simulation of Strongly Coupled 2+1D SU(2) Lattice Gauge Theory on a Honeycomb Lattice
We find a simple spin Hamiltonian to describe physical states of 2+1D SU(2) lattice gauge theory on a honeycomb lattice with a truncation of the electric field representation at j_max=1/2. The simple spin Hamiltonian only contains local products of Pauli matrices, even though Gauss’s law has been completely integrated out.
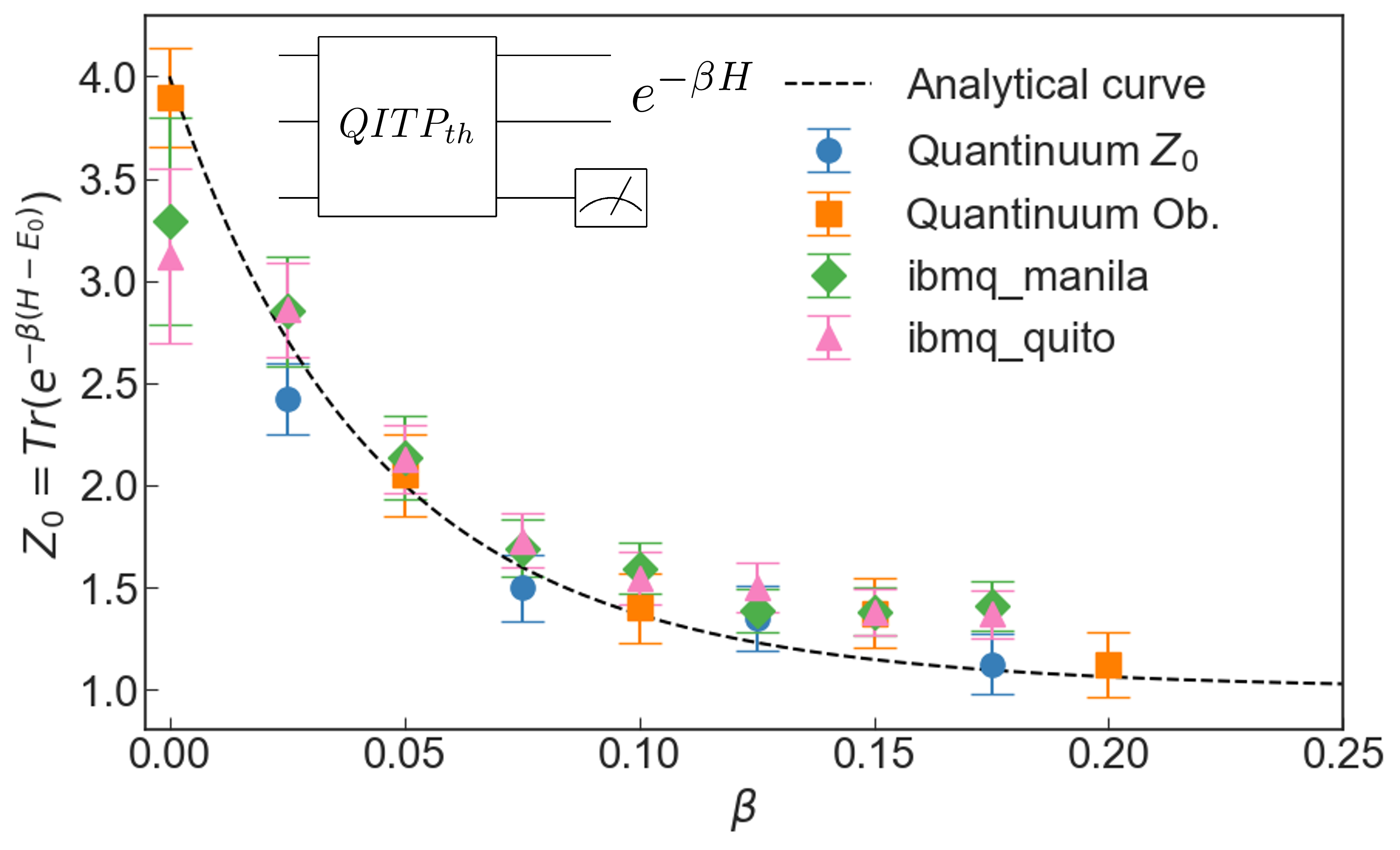
Quantum Imaginary Time Propagation algorithm for preparing thermal states
Calculations at finite temperatures are fundamental in different scientific fields, from nuclear physics to condensed matter. Evolution in imaginary time is a prominent classical technique for preparing thermal states of quantum systems. We propose a new quantum algorithm that prepares thermal states based on the quantum imaginary time propagation method, using a diluted operator with ancilla qubits to overcome the non-unitarity nature of the imaginary time operator. The presented method is the first that allows us to obtain the correct thermal density matrix on a general quantum processors for a generic Hamiltonian. We prove its reliability in the actual quantum hardware computing thermal properties for two and three neutron systems.
Multi-Body Entanglement and Information Rearrangement in Nuclear Many-Body Systems
The present work examines how effective-model-space calculations of nuclear many-body systems are able to rearrange and converge multi-particle entanglement, and information more generally. The generalized Lipkin-Meshkov-Glick (LMG) model is considered here as a demonstration, to motivate and provide insight for future developments of entanglement-driven descriptions of nuclei. The effective approach is based on a truncation of the Hilbert space to an effective model space, together with a variational rotation of the qubits (spins), which constitute the relevant elementary degrees of freedom in this model. The non-commutivity of the rotation and truncation allow for an exponential improvement of the energy convergence throughout much of the model space, compared with truncations without rotations, as we have shown previously in the reduced LMG model. Our analysis is extended to examine measures of correlations and entanglement, and to quantify their convergence with increasing cut-off. We focus on one- and two-spin entanglement entropies, mutual information, as well as n-tangles for n=2, 4 to estimate multi-body entanglement. The effective description is found to provide “minimal” entropies and mutual information of the rotated spins, while, at the same time, being able to recover the exact results to a large extent with low cut-offs. Naive truncations of the bare Hamiltonian, on the other hand, artificially underestimate these measures. The n-tangles in the present model provide a basis-independent measures of n-particle entanglement. While these are found to be more difficult to capture with the EMS description, the improvement in convergence, compared to truncations of the bare Hamiltonian, is significantly more dramatic. Finally, we investigate how spin squeezing, which is particularly sensitive to entanglement details of the system, is reproduced by quantum simulations of the LMG model we previously performed using IBM’s quantum computers. We conclude that the low-energy effective model space techniques, that successfully provide predictive capabilities for low-lying observables in many-body systems, exhibit analogous efficacy for quantum correlations and multi-body entanglement in the LMG model, motivating future studies in nuclear many-body systems that are closer to nature. We anticipate our results have import for effective field theories relevant to high-energy physics and nuclear physics more broadly.
This work was supported, in part, by Universit ̈at Bielefeld and ERC- 885281-KILONOVA Advanced Grant, and, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science.
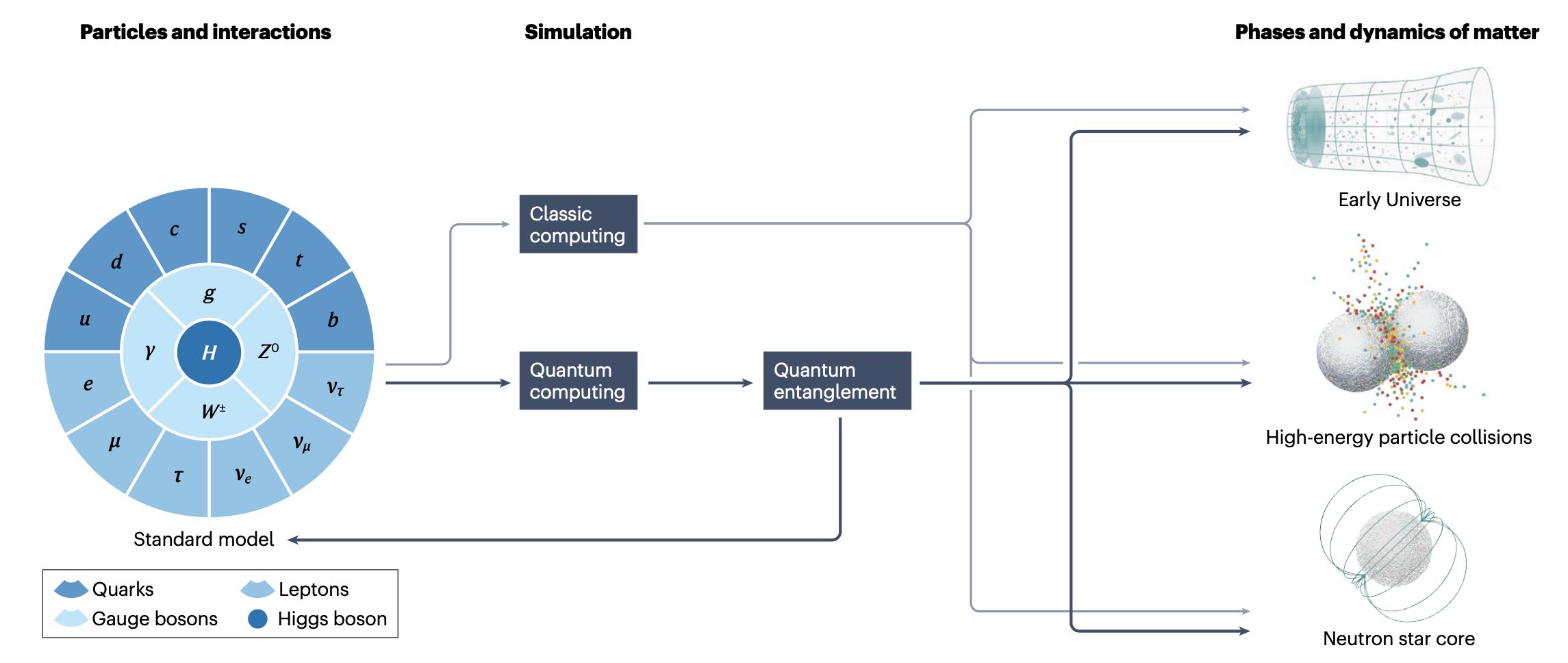
Quantum simulation of fundamental particles and forces
Key static and dynamic properties of matter — from creation in the Big Bang to evolution into subatomic and astrophysical environments — arise from the underlying fundamental quantum fields of the standard model and their effective descriptions. However, the simulation of these properties lies beyond the capabilities of classical computation alone. Advances in quantum technologies have improved control over quantum entanglement and coherence to the point at which robust simulations of quantum fields are anticipated in the foreseeable future. In this Perspective article, we discuss the emerging area of quantum simulations of standard-model physics, outlining the challenges and opportunities for progress in the context of nuclear and high-energy physics.
Real Time Quarkonium Transport Coefficients in Open Quantum Systems from Euclidean QCD
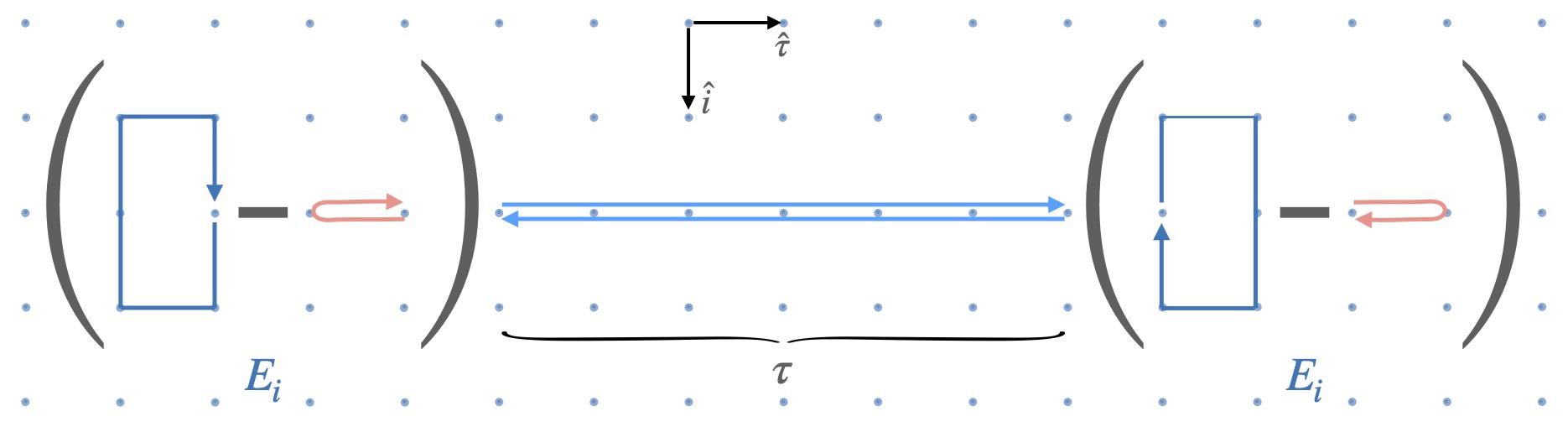
Recent open quantum system studies showed that quarkonium time evolution inside the quark-gluon plasma is determined by transport coefficients that are defined in terms of a gauge invariant correlator of two chromoelectric field operators connected by an adjoint Wilson line. We study the Euclidean version of the correlator for quarkonium evolution and discuss the extraction of the transport coefficients from this Euclidean correlator, highlighting its difference from other problems that also require reconstructing a spectral function, such as the calculation of the heavy quark diffusion coefficient. Along the way, we explain why the transport coefficient gamma(adj) differs from gamma(fund) at finite temperature at O(g^4), in spite of the fact that their corresponding spectral functions differ only by a temperature-independent term at the same order. We then discuss how to evaluate the Euclidean correlator via lattice QCD methods, with a focus on reducing the uncertainty caused by infrared renormalons in determining the renormalization factor nonperturbatively.
High-energy Collision of Quarks and Hadrons in the Schwinger Model: From Tensor-Networks to Circuit-QED
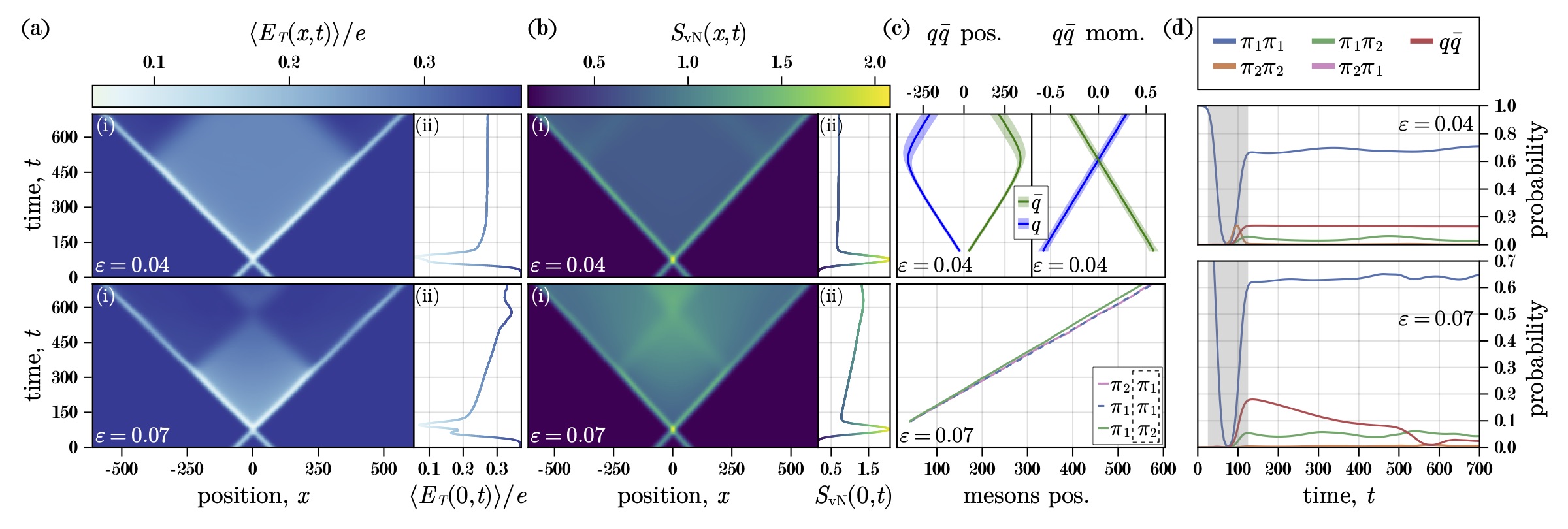
With the aim of studying nonperturbative, out-of-equilibrium dynamics of high-energy particle collisions on quantum simulators, we investigate the scattering dynamics of lattice quantum electrodynamics in 1+1 dimensions. Working in the bosonized formulation of the model, an analog circuit-QED implementation is proposed that is native to the platform, hence requires minimal ingredients and approximations, and enables practical schemes for particle wavepacket preparation and evolution. Furthermore, working in the thermodynamic limit, uniform-matrix-product-state tensor networks are used to construct multi-particle wavepacket states, evolve them in time, and detect outgoing particles post collision. This facilitates the numerical simulation of scattering experiments in both confined and deconfined regimes of the model at different energies, giving rise to rich phenomenology, including inelastic production of quark and meson states, meson disintegration, and dynamical string formation and breaking. Elastic and inelastic scattering cross sections are obtained, together with time-resolved momentum and position distributions of the outgoing particles. This study highlights the role of classical and quantum simulation in enhancing our understanding of scattering processes in quantum field theories in real time.
Quantum Simulations of SO(5) Many-Fermion Systems using Qudits
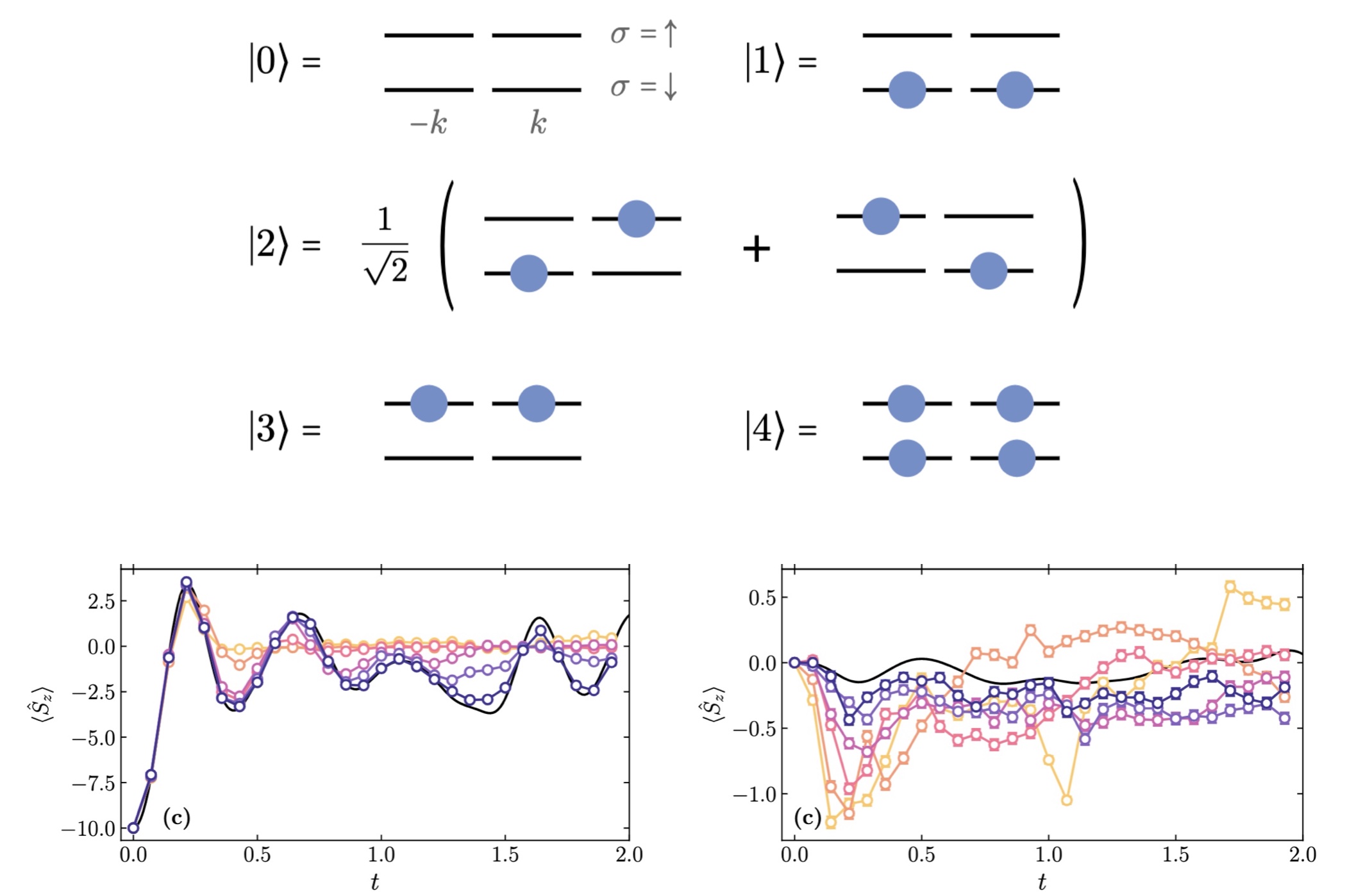
The structure and dynamics of many-body systems are the result of a delicate interplay between underlying interactions. Fermionic pairing plays a central role in various physical systems and can lead to collective phenomena such as superconductivity and superfluidity. We explore the potential utility of quantum computers with arrays of qudits in simulating interacting fermionic systems, when the qudits can be naturally mapped to the relevant degrees of freedom. The Agassi model of fermions is based on an underlying $so(5)$ algebra, and the systems it describes can be partitioned into pairs of modes with five basis states, which naturally embed in arrays of $d=5$ qudits (qu5its). Classical noiseless simulations of the time evolution of systems of fermions embedded in up to twelve qu5its are performed using Google’s {\tt cirq} software. The resource requirements of the qu5it circuits are analyzed and compared with two different mappings to qubit systems, a physics-aware Jordan-Wigner mapping and a state-to- state mapping. We find advantages in using qudits, specifically in lowering the required quantum resources and reducing anticipated errors that take the simulation out of the physical space. A previously unrecognized sign problem has been identified from Trotterization errors in time evolving high-energy excitations. This has implications for quantum simulations in high energy and nuclear physics, specifically of fragmentation and highly inelastic, multi-channel processes.
This work was supported, in part, by Universität Bielefeld and ERC- 885281-KILONOVA Advanced Grant (Robin), by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 (Savage), and the Quantum Science Center (QSC), a National Quantum Information Science Research Center of the U.S. Department of Energy (Illa).
Randomized measurement protocols for lattice gauge theories
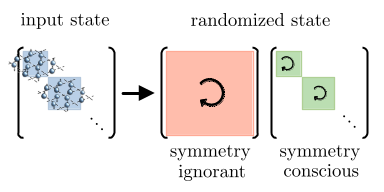
Randomized measurement protocols, including classical shadows, entanglement tomography, and randomized benchmarking are powerful techniques to estimate observables, perform state tomography, or extract the entanglement properties of quantum states. While unraveling the intricate structure of quantum states is generally difficult and resource-intensive, quantum systems in nature are often tightly constrained by symmetries. This can be leveraged by the symmetry-conscious randomized measurement schemes we propose, yielding clear advantages over symmetry-blind randomization such as reducing measurement costs, enabling symmetry-based error mitigation in experiments, allowing differentiated measurement of (lattice) gauge theory entanglement structure, and, potentially, the verification of topologically ordered states in existing and near-term experiments. Crucially, unlike symmetry-blind randomized measurement protocols, these latter tasks can be performed without relearning symmetries via full reconstruction of the density matrix.
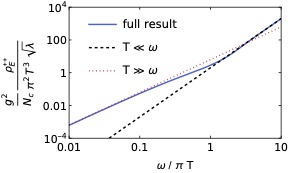
Chromoelectric field correlator for quarkonium transport in the strongly coupled N=4 Yang-Mills plasma from AdS/CFT
Previous studies have shown that a gauge-invariant correlation function of two chromoelectric fields connected by a straight timelike adjoint Wilson line encodes crucial information about quark-gluon plasma (QGP) that determines the dynamics of small-sized quarkonium in the medium. Motivated by the successes of holographic calculations to describe strongly coupled QGP, we calculate the analog gauge-invariant correlation function in strongly coupled $\mathcal{N}=4$ supersymmetric Yang-Mills theory at finite temperature by using the AdS/CFT correspondence. Our results indicate that the transition processes between bound and unbound quarkonium states are suppressed in strongly coupled plasmas, and moreover, the leading contributions to these transition processes vanish in both the quantum Brownian motion and quantum optical limits of open quantum system approaches to quarkonia.
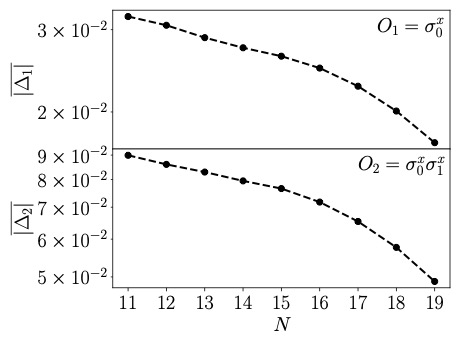
SU(2) Non-Abelian Gauge Theory on a Plaquette Chain Obeys Eigenstate Thermalization Hypothesis
We test the eigenstate thermalization hypothesis (ETH) for 2+1 dimensional SU(2) lattice gauge theory. By considering the theory on a chain of plaquettes and truncating basis states for link variables at j=1/2, we can map it onto an Ising chain and numerically exactly diagonalize the Hamiltonian for reasonably large lattice sizes. We find energy level repulsion in momentum sectors with no remaining discrete symmetries. We study two local observables made up of Wilson loops and calculate their matrix elements in the energy eigenbasis, which are shown consistent with the ETH. Our study implies a subset of states in the physical Hilbert space of Quantum Chromodynamics (QCD) obeys the ETH.


