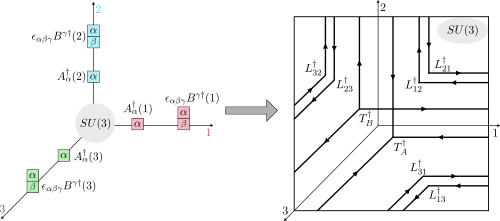
The construction of gauge invariant states of SU(3) lattice gauge theories has garnered new interest in recent years, but implementing them is complicated by the difficulties of SU(3) Clebsch-Gordon coefficients. In the loop-string-hadron (LSH) approach to lattice gauge theories, the elementary excitations are strictly gauge invariant, and constructing the basis requires no knowledge of Clebsch-Gordon coefficients. Originally developed for SU(2), the LSH formulation was recently generalized to SU(3), but limited to one spatial dimension. In this work, we generalize the LSH approach to constructing the basis of SU(3) gauge invariant states at a trivalent vertex — the essential building block to multidimensional space. A direct generalization from the SU(2) vertex yields a legitimate basis; however, in certain sectors of the Hilbert space, the naive LSH basis vectors so defined suffer from being nonorthogonal. The issues with orthogonality are directly related to the “missing label” or “outer multiplicity” problem associated with SU(3) tensor products, and may also be phrased in terms of Littlewood-Richardson coefficients or the need for a “seventh Casimir” operator. The states that are unaffected by the problem are orthonormalized in closed form. For the sectors that are afflicted, we discuss the nonorthogonal bases and their orthogonalization. A few candidates for seventh Casimir operators are readily constructed from the suite of LSH gauge-singlet operators. The diagonalization of a seventh Casimir represents one prescriptive solution towards obtaining a complete orthonormal basis, but a closed-form general solution remains to be found.