IQuS Publications

On Quantum Simulation of QED in Coulomb Gauge
A recent work (Li, 2406.01204) considered quantum simulation of Quantum Electrodynamics (QED) on a lattice in the Coulomb gauge with gauge degrees of freedom represented in the occupation basis in momentum space. Here we consider representing the gauge degrees of freedom in field basis in position space and develop a quantum algorithm for real-time simulation. We show that the Coulomb gauge Hamiltonian is equivalent to the temporal gauge Hamiltonian when acting on physical states consisting of fermion and transverse gauge fields. The Coulomb gauge Hamiltonian guarantees that the unphysical longitudinal gauge fields do not propagate and thus there is no need to impose any constraint. The local gauge field basis and the canonically conjugate variable basis are swapped efficiently using the quantum Fourier transform. We prove that the qubit cost to represent physical states and the gate depth for real-time simulation scale polynomially with the lattice size, energy, time, accuracy and Hamiltonian parameters. We focus on the lattice theory without discussing the continuum limit or the UV completion of QED.
Parton Distributions on a Quantum Computer
We perform the first quantum computation of parton distribution function (PDF) with a real quantum device by calculating the PDF of the lightest positronium in the Schwinger model with IBM quantum computers. The calculation uses 10 qubits for staggered fermions at five spatial sites and one ancillary qubit. The most critical and challenging step is to reduce the number of two-qubit gate depths to around 500 so that sensible results start to emerge. The resulting lightcone correlators have excellent agreement with the classical simulator result in central values, although the error is still large. Compared with classical approaches, quantum computation has the advantage of not being limited in the accessible range of parton momentum fraction x due to renormalon ambiguity, and the difficulty of accessing non-valence partons. A PDF calculation with 3+1 dimensional QCD near x=0 or x=1 will be a clear demonstration of the quantum advantage on a problem with great scientific impact.
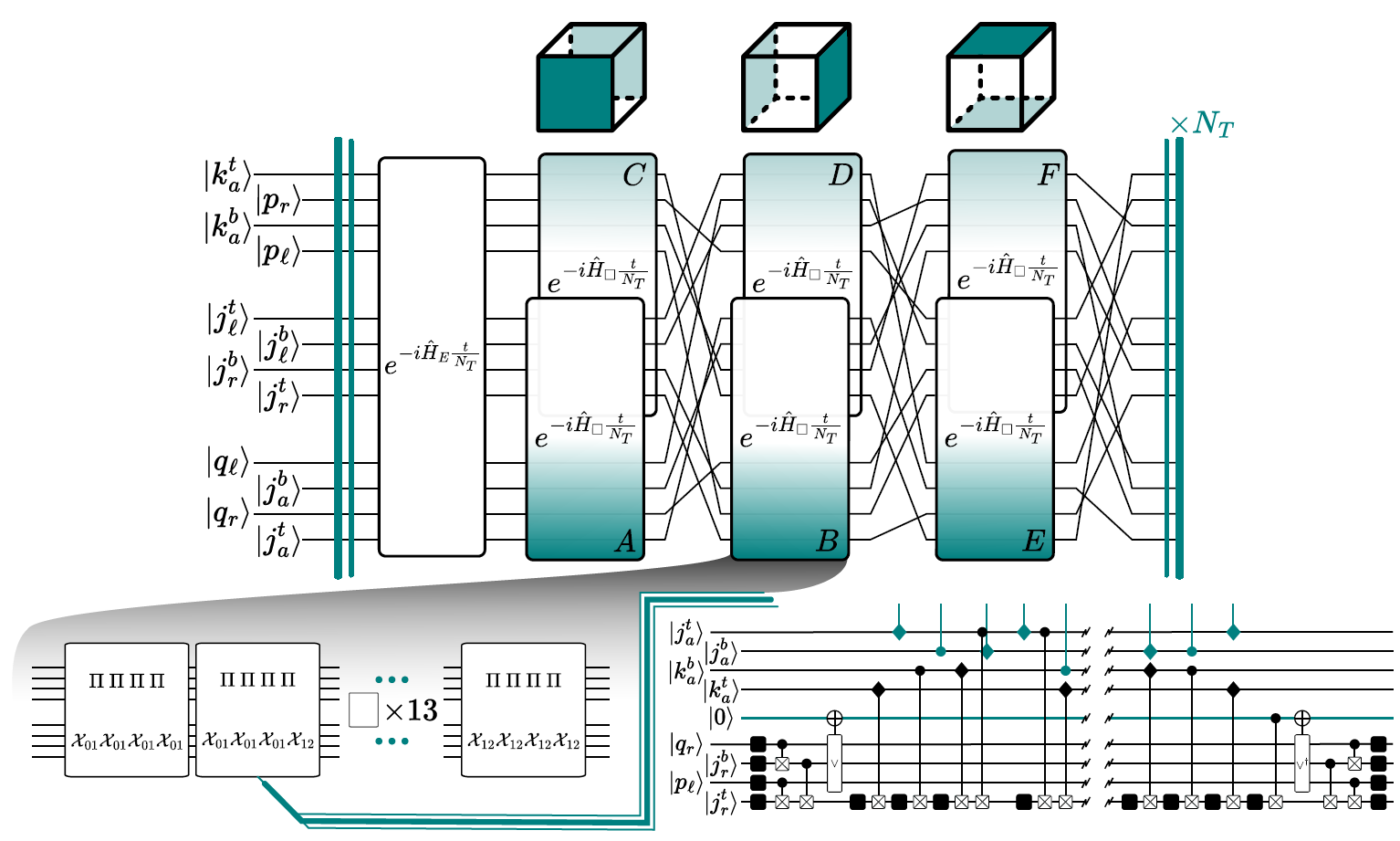
Non-Abelian Dynamics on a Cube: Improving Quantum Compilation through Qudit-Based Simulations
Recent developments in mapping lattice gauge theories relevant to the Standard Model onto digital quantum computers identify scalable paths with well-defined quantum compilation challenges toward the continuum. As an entry point to these challenges, we address the simulation of SU(2) lattice gauge theory. Using qudit registers to encode the digitized gauge field, we provide quantum resource estimates, in terms of elementary qudit gates, for arbitrarily high local gauge field truncations. We then demonstrate an end-to-end simulation of real-time, qutrit-digitized SU(2) dynamics on a cube. Through optimizing the simulation, we improved circuit decompositions for uniformly-controlled qudit rotations, an algorithmic primitive for general applications of quantum computing. The decompositions also apply to mixed-dimensional qudit systems, which we found advantageous for compiling lattice gauge theory simulations. Furthermore, we parallelize the evolution of opposite faces in anticipation of similar opportunities arising in three-dimensional lattice volumes. This work details an ambitious executable for future qudit hardware and attests to the value of codesign strategies between lattice gauge theory simulation and quantum compilation.
This collaboration was funded by the NSERC Alliance International Catalyst Quantum Grant program (ALLRP 586483-23). JJ is funded in part by the NSERC CREATE in Quantum Computing Program, grant number 543245. NK acknowledges funding in part from the NSF STAQ Program (PHY-1818914). ODM acknowledges funding from NSERC, the Canada Research Chairs Program, and UBC. This work was conceived at the 2023 Quantum Computing, Quantum Simulation, Quan- tum Gravity and the Standard Model workshop at the InQubator for Quantum Simulation (IQuS) hosted by the Institute for Nuclear Theory (INT). IQuS is supported by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science, and by the Department of Physics, and the College of Arts and Sciences at the University of Washington.
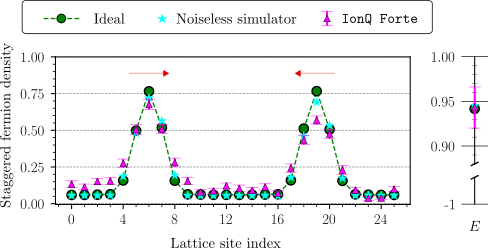
Pathfinding Quantum Simulations of Neutrinoless Double-Beta Decay
We present results from co-designed quantum simulations of the neutrinoless double-beta decay of a two-hadron nucleus in 1+1D quantum chromodynamics using IonQ’s Forte-generation trapped-ion quantum computers. Two flavors of dynamical quarks and leptons are distributed across two lattice sites and mapped to 32 qubits. An effective four-Fermi contact interaction is used to implement charged-current weak interactions between quarks and leptons, and lepton-number violation is induced by a neutrino Majorana mass. Statistically-significant signals for the neutrinoless decay of a two-hadron nucleus are measured during time evolution with a non-zero Majorana mass, making this the first quantum simulation to observe lepton-number violation in real time. This was made possible by co-designing the state preparation and time evolution quantum circuits to maximally utilize the all-to-all connectivity and native gate-set available on IonQ’s quantum computers. Quantum circuit compilation techniques and symmetry-aware error-mitigation methods, tailored to neutrinoless decays, allow accurate results to be extracted from quantum circuits with up to 470 two-qubit gates using Forte Enterprise. We present first benchmarks toward the real-time simulation of neutrinoless double-beta decay, and discuss the potential of future quantum simulations to provide yocto-second resolution of the reaction pathway for nuclear processes.
We would like to thank Saurabh Kadam for helpful discussions. This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (MJS, IC, RCF), and by the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (MI, IC). This work is also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington. RCF acknowledges support from the U.S. Department of Energy QuantISED program through the theory consortium “Intersections of QIS and Theoretical Particle Physics” at Fermilab, from the U.S. Department of Energy, Office of Science, Accelerated Research in Quantum Computing, Quantum Utility through Advanced Computational Quantum Algorithms (QUACQ), and from the Institute for Quantum Information and Matter, an NSF Physics Frontiers Center (PHY-2317110). RCF additionally acknowledges support from a Burke Institute prize fellowship. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0032083. AM, FT, MALR, AA, YDS, AB, CG, AK and MR are employees and equity holders of IonQ, Inc.
Quantum computation of hadron scattering in a lattice gauge theory
We present a digital quantum computation of two-hadron scattering in a Z2 lattice gauge theory in 1+1 dimensions. We prepare well-separated single-particle wave packets with desired momentum-space wavefunctions, and simulate their collision through digitized time evolution. Multiple hadronic wave packets can be produced using the systematically improvable algorithm of this work, achieving high fidelity with the target initial state, and demanding only polynomial resources in system size. Specifically, employing a trapped-ion quantum computer (IonQ Forte), we prepare up to three meson wave packets\ using 11 and 27 system qubits, and simulate collision dynamics of two meson wave packets for the smaller system. Despite noise effects, post-processing with a global-symmetry-based noise mitigation yields results consistent with numerical simulations, but decoherence limits evolution into long times. We demonstrate the critical role of high-fidelity initial states for precision measurements of state-sensitive observables, such as S-matrix elements and decay amplitudes. While we have not established quantum advantage by this early hardware demonstration, our algorithms are general, and our findings imply the potential of quantum computers in simulating scattering processes in strongly interacting gauge theories.
Quantum-emulator and quantum-hardware computations of this work were enabled by access to IonQ systems provided by the University of Maryland’s National Quantum Laboratory (QLab). We thank support from IonQ scientists and engineers, especially Daiwei Zhu, during the execution of our runs. We further thank Franz Klein at QLab for the help in setting up access and communications with IonQ contacts. S.K. acknowledges valuable discussions with Roland Farrell and Francesco Turro. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. The numerical results in this work were obtained using Qiskit [204], ITensors [205], Julia [206] and Jupyter Notebook [207] software applications within the Conda [208] environment.
Z.D. and C-C.H. acknowledge support from the National Science Foundation’s Quantum Leap Challenge Institute on Robust Quantum Simulation (award no. OMA-2120757); the U.S. Department of Energy (DOE), Office of Science, Early Career Award (award no. DESC0020271); and the Department of Physics, Maryland Center for Fundamental Physics, and College of Computer, Mathematical, and Natural Sciences at the University of Maryland, College Park. Z.D. is further grateful for the hospitality of Nora Brambilla, and of the Excellence Cluster ORIGINS at the Technical University of Munich, where part of this work was carried out. The research at ORIGINS is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy (EXC-2094—390783311). S.K. acknowledges support by the U.S. DOE, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (award no. DE-SC0020970), and by the DOE QuantISED program through the theory consortium “Intersections of QIS and Theoretical Particle Physics” at Fermilab (Fermilab subcontract no. 666484). This work was also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington.

Quarkonia Theory: From Open Quantum System to Classical Transport
This is a theoretical overview of quarkonium production in relativistic heavy ion collisions given for the Hard Probe 2024 conference at Nagasaki. The talk focuses on the application of the open quantum system framework and the formulation of the chromoelectric correlator that uniquely encodes properties of the quark-gluon plasma relevant for quarkonium dynamics and thus can be extracted from theory-experiment comparison.
This work is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science.
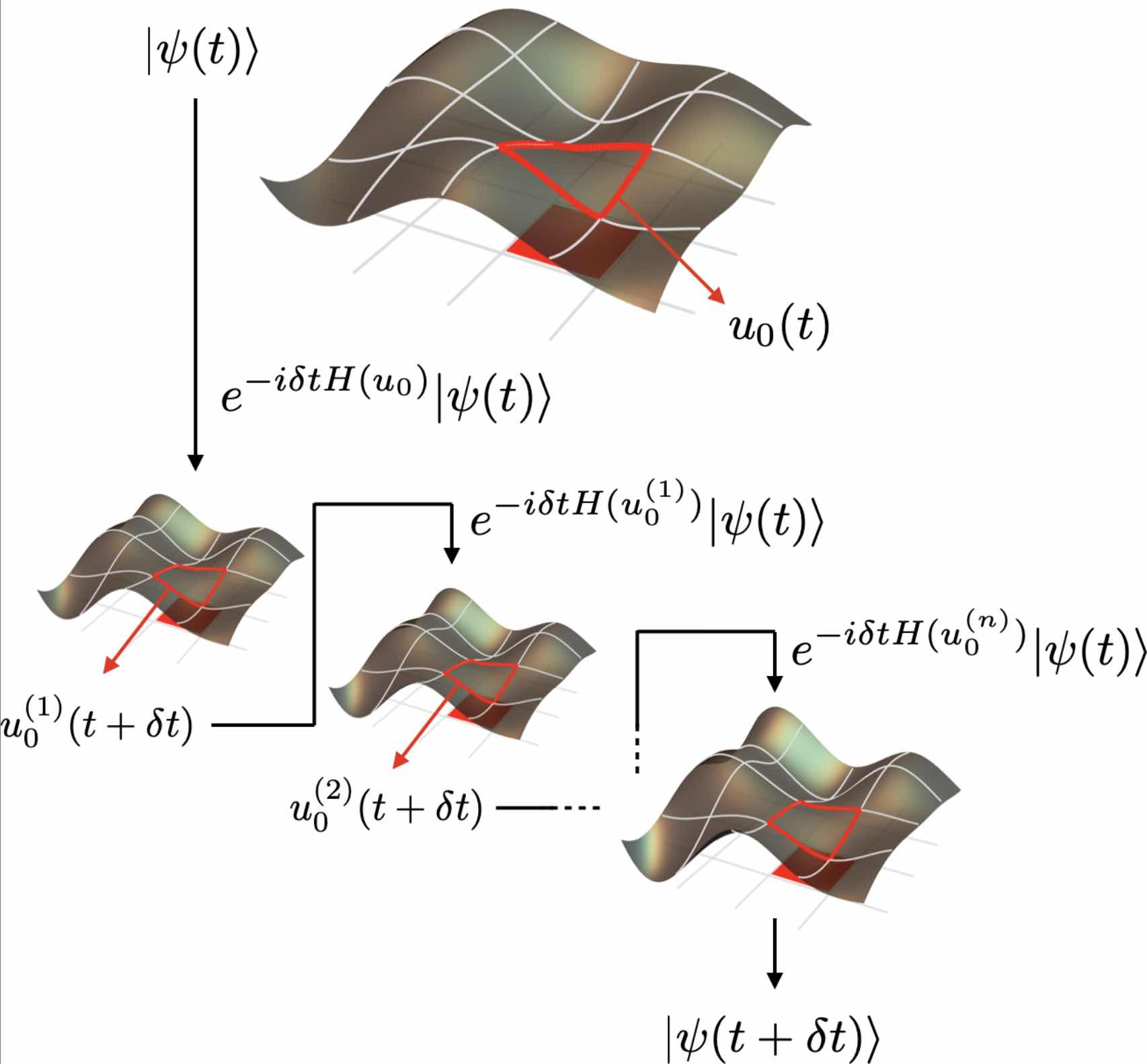
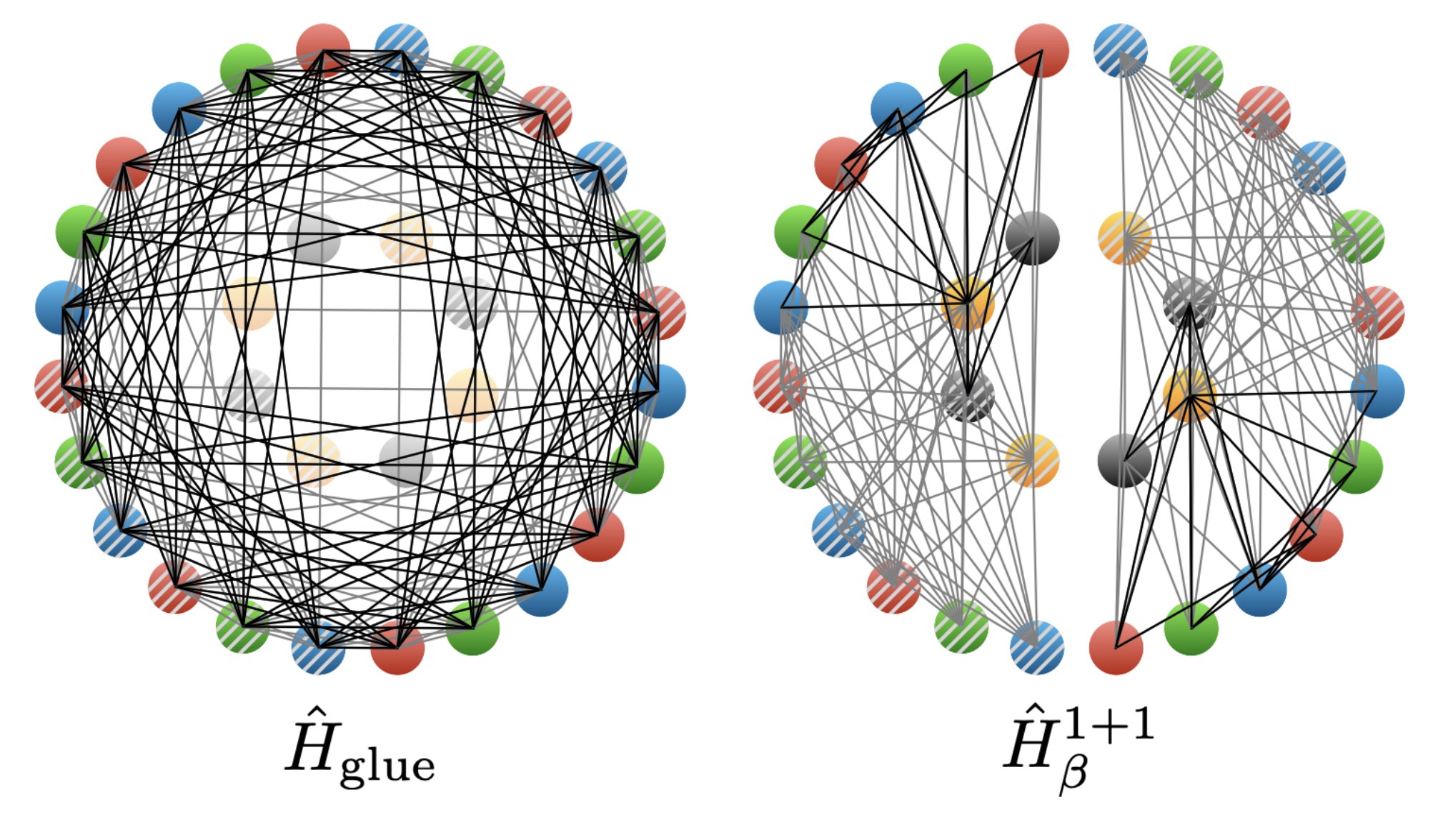
Dynamical Local Tadpole-Improvement in Quantum Simulations of Gauge Theories
We identify a new element in quantum simulations of lattice gauge theories, arising from spacetime-dependent quantum corrections in the relation between the link variables defined on the lattice and their continuum counterparts. While in Euclidean spacetime simulations, based on Monte Carlo sampling, the corresponding tadpole improvement leads to a constant rescaled value per gauge configuration, in Minkowski spacetime simulations it requires a state- and time dependent update of the coefficients of operators involving link variables in the Hamiltonian. To demonstrate this effect, we present the results of numerical simulations of the time evolution of truncated SU(2) plaquette chains and honeycomb lattices in 2+1D, starting from excited states with regions of high energy density, and with and without entanglement.
We would like to thank Randy Lewis for helpful discussions regarding the classical implementation of tadpole improvement. This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Martin, Xiaojun), and by the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (Marc). This work is also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington. We have made extensive use of Wolfram Mathematica. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0032083.
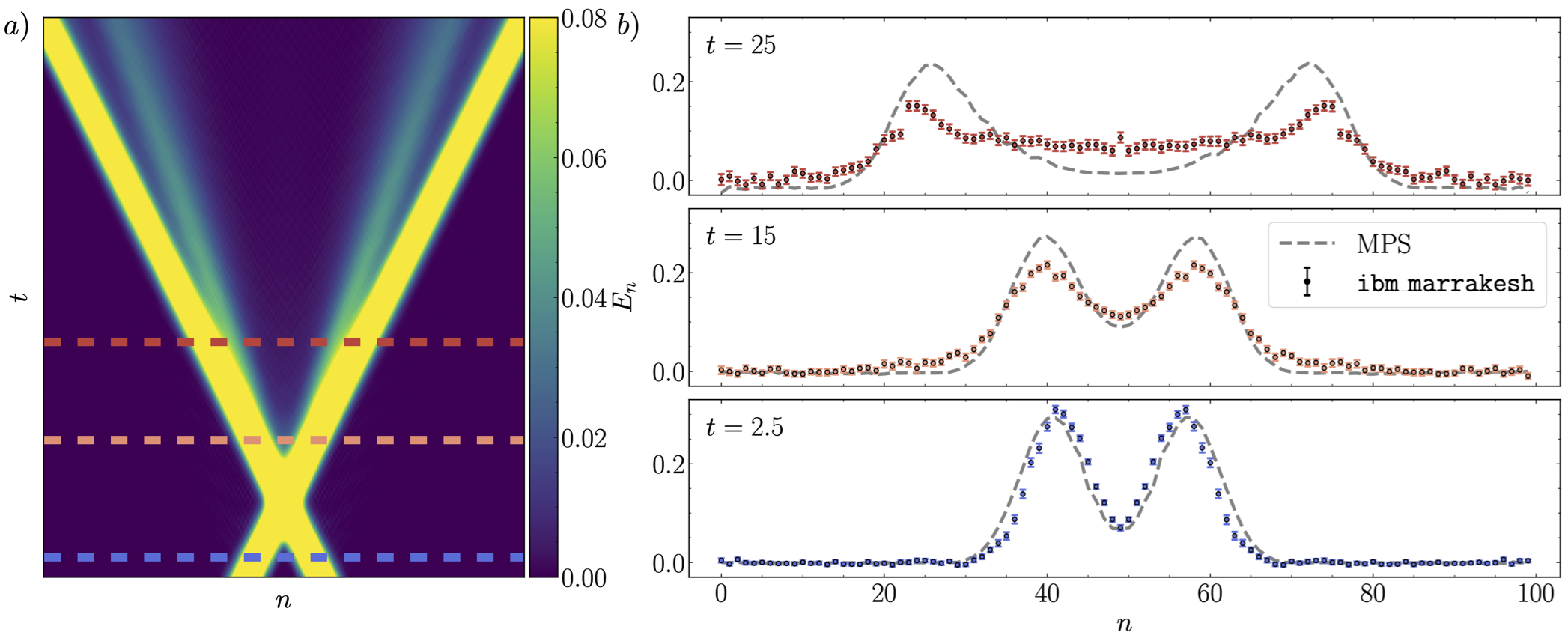
Digital Quantum simulations of particle collisions in quantum field theories using W states
A new quantum algorithm for preparing the initial state (wavepackets) of a quantum field theory scattering simulation is introduced. This method extends recent techniques for preparing W states using mid-circuit measurement and feedforward to efficiently create wavepackets. The required circuit depth is independent of wavepacket size, representing a superexponential improvement over previous methods. Explicit examples are provided for one-dimensional Ising field theory, scalar field theory, the Schwinger model, and two dimensional Ising field theory. The circuits that prepare wavepackets in one-dimensional Ising field theory are used to simulate scattering on 100 qubits of IBM’s quantum computer ibm_marrakesh. Quantum simulations are performed at a center of mass energy above inelastic threshold, and measurements of the energy density in the post-collision state reveal the production of new particles. A novel error mitigation strategy based on energy conservation enables accurate results to be extracted from circuits with up to 6,412 two-qubit gates. The prospects for a near-term quantum advantage in simulations of scattering are discussed.
We would like to thank Ivan Chernyshev, David Simmons-Duffin, Johnnie Gray, Ash Milsted, Martin Sav- age and Federica Surace for helpful discussions. RF and JP acknowledge support from the U.S. Department of Energy QuantISED program through the theory consortium “Intersections of QIS and Theoretical Particle Physics” at Fermilab, from the U.S. Department of Energy, Office of Science, Accelerated Research in Quantum Computing, Quantum Utility through Advanced Computational Quantum Algorithms (QUACQ), and from the Institute for Quantum Information and Matter, an NSF Physics Frontiers Center (PHY-2317110). RF additionally acknowledges support from a Burke Institute prize fellowship. NZ acknowledges support provided by the DOE, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the pro- gram on Quantum Horizons: QIS Research and Innovation for Nuclear Science. NZ is also supported by the Department of Physics and the College of Arts and Sciences at the University of Washington. MI acknowledges support provided by the Quantum Science Center (QSC), which is a National Quantum Information Science Research Center of the U.S. Department of Energy. JP acknowledges funding provided by the U.S. Department of Energy Office of High Energy Physics (DE-SC0018407), the U.S. Department of Energy, Office of Science, Accelerated Research in Quantum Computing, Fundamental Algorithmic Research toward Quantum Utility (FAR- Qu), and the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Quantum Systems Accelerator. The computations presented in this work were conducted in the Resnick High Performance Computing Center, a facility supported by the Resnick Sustainability Institute at Caltech and also enabled by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. RF and NZ acknowledge the use of IBM Quantum Credits for this work. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team.

Quarkonium suppression in strongly coupled plasmas
Suppression of open heavy quarks and quarkonia in heavy-ion collisions are among the most informative probes of quark-gluon plasma (QGP). Interpreting the full wealth of data obtained from the collision events requires a precise theoretical understanding of the evolution of heavy quarks and quarkonia as they propagate through a strongly coupled plasma. Such calculations require the evaluation of a gauge-invariant correlator of chromoelectric fields. This chromoelectric correlator encodes all the characteristics of QGP that the dissociation and recombination dynamics of quarkonium are sensitive to, which is to say can in principle measure. We review its distinctive qualitative features at weak coupling in QCD up to next-to-leading order and at strong coupling in $\mathcal{N}=4$ SYM using the AdS/CFT correspondence, as well as its formulation in Euclidean QCD. Furthermore, we report on recent progress in applying our results to the calculation of the final quarkonium abundances after propagating through a cooling droplet of QGP, which illustrates how we may learn about QGP from quarkonium measurements. We devote special attention to how the presence of a strongly coupled plasma modifies the transport description of quarkonium, in comparison to approaches that rely on weak coupling approximations to describe quarkonium dissociation and recombination.
The work of BSH is supported by grant NSF PHY-2309135 to the Kavli Institute for Theoretical Physics (KITP), and by grant 994312 from the Simons Foundation. XY is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science.
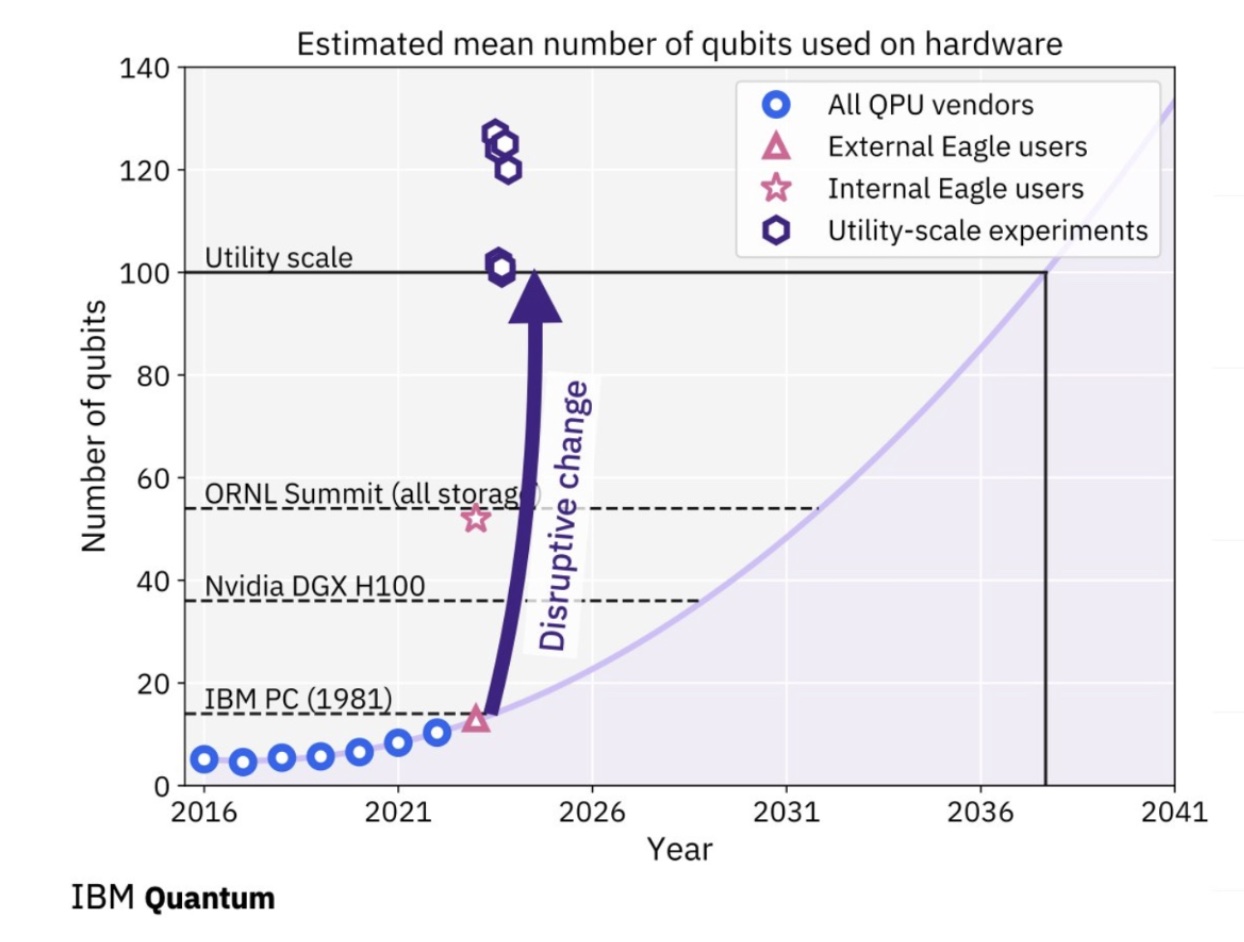
Quantum Simulations of Fundamental Physics
Simulating the dynamics of non-equilibrium matter under extreme conditions lies beyond the capabilities of classical computation alone. Remarkable advances in quantum information science and technology are profoundly changing how we understand and explore fundamental quantum many-body systems, and have brought us to the point of simulating essential aspects of these systems using quantum computers. I discuss highlights, opportunities and the challenges that lie ahead.


