IQuS Publications
Improved Honeycomb and Hyper-Honeycomb Lattice Hamiltonians for Quantum Simulations of Non-Abelian Gauge Theories
Improved Kogut-Susskind Hamiltonians for quantum simulations of non-Abelian Yang-Mills gauge theories are developed for honeycomb (2+1D) and hyper-honeycomb (3+1D) spatial tessellations. This is motivated by the desire to identify lattices for quantum simulations that involve only 3-link vertices among the gauge field group spaces in order to reduce the complexity in applications of the plaquette operator. For the honeycomb lattice, we derive a classically O(b²)-improved Hamiltonian, with b being the lattice spacing. Tadpole improvement via the mean-field value of the plaquette operator is used to provide the corresponding quantum improvements. We have identified the (non-chiral) hyper-honeycomb as a candidate spatial tessellation for 3+1D quantum simulations of gauge theories, and determined the associated O(b)-improved Hamiltonian.
This work was supported, in part, by the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S. Department of Energy (Marc), and by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science (Martin, Xiaojun).

Quarkonium Polarization Kinetic Equation from Open Quantum Systems and Effective Field Theories
Recent measurements of polarization phenomena in relativistic heavy ion collisions have aroused a great interest in understanding dynamical spin evolution of the QCD matter. In particular, the spin alignment signature of $J/\psi$ has been recently observed in Pb-Pb collisions at LHC, which may infer nontrivial spin transport of quarkonia in quark gluon plasmas. Motivated by this, we study the spin-dependent in-medium dynamics of quarkonia by using the potential nonrelativistic QCD (pNRQCD) and the open quantum system framework. By applying the Markovian approximation and Wigner transformation, we systematically derive the Boltzmann transport equation for vector quarkonia with polarization dependence in the quantum optical limit. As opposed to the previous study for the spin-independent case where the collision terms depend on chromoelectric correlators, the new kinetic equation incorporates gauge invariant correlators of chromomagnetic fields that determine the recombination and dissociation terms with polarization dependence at the order we are working in the multipole expansion. In the quantum Brownian motion limit, the Lindblad equation with new transport coefficients defined in terms of the chromomagnetic field correlators have also been derived. Our formalism is generic and valid for both weakly-coupled and strongly-coupled quark gluon plasmas. It may be further applied to study spin alignment of vector quarkonia in heavy ion collisions.

Emergent Hydrodynamic Mode on SU(2) Plaquette Chains and Quantum Simulation
We search for emergent hydrodynamic modes in real-time Hamiltonian dynamics of $2+1$-dimensional SU(2) lattice gauge theory on a quasi one dimensional plaquette chain, by numerically computing symmetric correlation functions of energy densities on lattice sizes of about $20$ with the local Hilbert space truncated at $j_{\rm max}=\frac{1}{2}$. Due to the Umklapp processes, we only find a mode for energy diffusion. The symmetric correlator exhibits transport peak near zero frequency with a width proportional to momentum squared at small momentum, when the system is fully quantum ergodic, as indicated by the eigenenergy level statistics. This transport peak leads to a power-law $t^{-\frac{1}{2}}$ decay of the symmetric correlator at late time, also known as the long-time tail, as well as diffusion-like spreading in position space. We also introduce a quantum algorithm for computing the symmetric correlator on a quantum computer and find it gives results consistent with exact diagonalization when tested on the IBM emulator. Finally we discuss the future prospect of searching for the sound modes.

Work and heat exchanged during sudden quenches of strongly coupled quantum systems
How should one define thermodynamic quantities (internal energy, work, heat, etc.) for quantum systems coupled to their environments strongly? We examine three (classically equivalent) definitions of a quantum system’s internal energy under strong-coupling conditions. Each internal-energy definition implies a definition of work and a definition of heat. Our study focuses on quenches, common processes in which the Hamiltonian changes abruptly. In these processes, the first law of thermodynamics holds for each set of definitions by construction. However, we prove that only two sets obey the second law. We illustrate our findings using a simple spin model. Our results guide studies of thermodynamic quantities in strongly coupled quantum systems.
This work was supported by the DOE, Office of Science, Office of Nuclear Physics, IQuS (\url{https://iqus.uw.edu}), via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science under Award DE-SC0020970; and by the National Science Foundation (NSF) Quantum Leap Challenge Institutes (QLCI) (award no.~OMA-2120757); and by the Department of Energy (DOE), Office of Science, Early Career Award (award no.~DESC0020271), as well as by the Department of Physics; Maryland Center for Fundamental Physics; and College of Computer, Mathematical, and Natural Sciences at the University of Maryland, College Park. Part of this work was supported i by the Government of Canada through the Department of Innovation, Science, and Economic Development and by the Province of Ontario through the Ministry of Colleges and Universities; and by the Simons Foundation through the Simons Foundation Emmy Noether Fellows Program at Perimeter InstituteThe work was supported in part by the NSF award PHY-2309135 and by the John Templeton Foundation (award no.~62422).
The Present and Future of QCD
This White Paper presents the community inputs and scientific conclusions from the Hot and Cold QCD Town Meeting that took place September 23-25, 2022 at MIT, as part of the Nuclear Science Advisory Committee (NSAC) 2023 Long Range Planning process. A total of 424 physicists registered for the meeting. The meeting highlighted progress in Quantum Chromodynamics (QCD) nuclear physics since the 2015 LRP (LRP15) and identified key questions and plausible paths to obtaining answers to those questions, defining priorities for our research over the coming decade. In defining the priority of outstanding physics opportunities for the future, both prospects for the short (~ 5 years) and longer term (5-10 years and beyond) are identified together with the facilities, personnel and other resources needed to maximize the discovery potential and maintain United States leadership in QCD physics worldwide. This White Paper is organized as follows: In the Executive Summary, we detail the Recommendations and Initiatives that were presented and discussed at the Town Meeting, and their supporting rationales. Section 2 highlights major progress and accomplishments of the past seven years. It is followed, in Section 3, by an overview of the physics opportunities for the immediate future, and in relation with the next QCD frontier: the EIC. Section 4 provides an overview of the physics motivations and goals associated with the EIC. Section 5 is devoted to the workforce development and support of diversity, equity and inclusion. This is followed by a dedicated section on computing in Section 6. Section 7 describes the national need for nuclear data science and the relevance to QCD research.
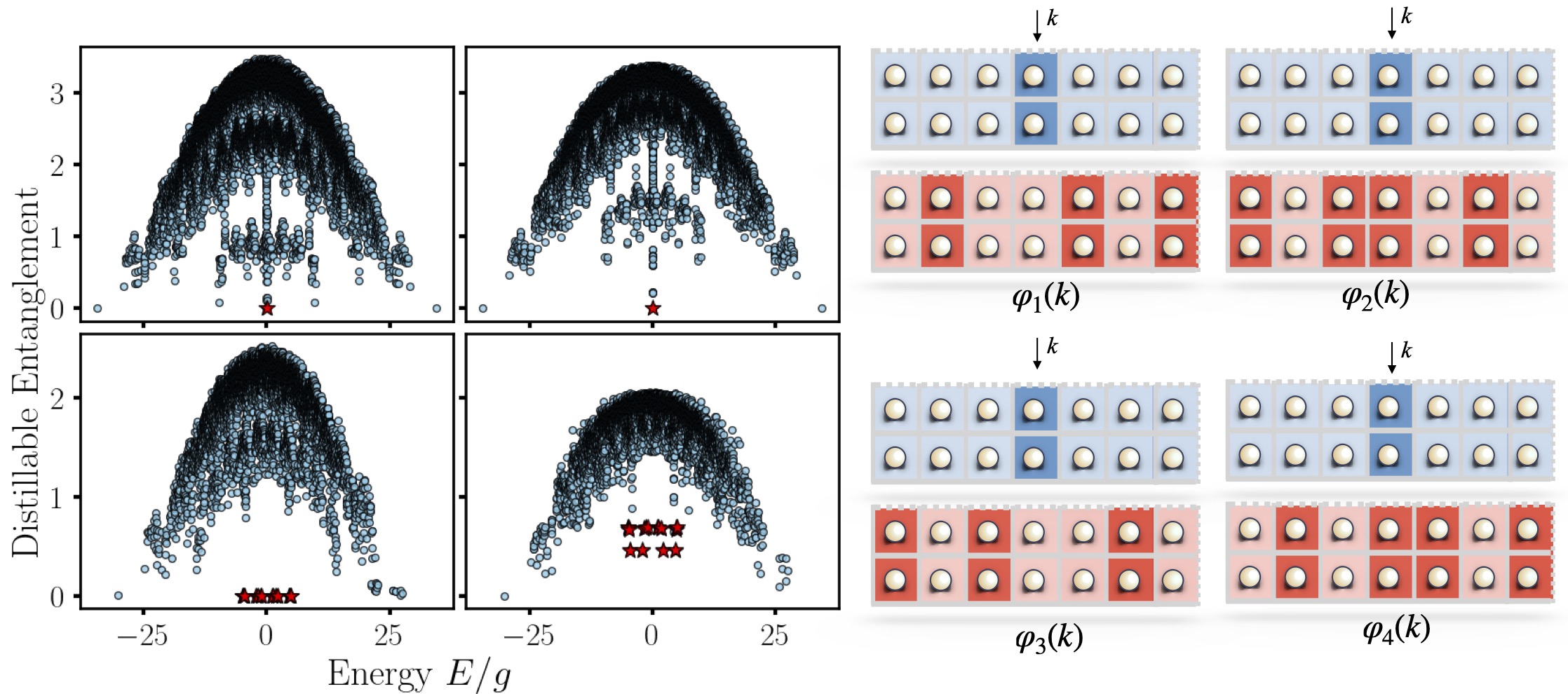
Stabilizer Scars
Quantum many-body scars are eigenstates in non-integrable isolated quantum systems that defy typical thermalization paradigms, violating the eigenstate thermalization hypothesis and quantum ergodicity. We identify exact analytic scar solutions in a 2+1 dimensional lattice gauge theory in a quasi-1d limit as zero-magic stabilizer states. We propose a protocol for their experimental preparation, presenting an opportunity to demonstrate a quantum over classical advantage via simulating the non-equilibrium dynamics of a strongly coupled system. Our results also highlight the importance of magic for gauge theory thermalization, revealing a connection between computational complexity and quantum ergodicity.
This work is supported by the DOE, Office of Science, Office of Nuclear Physics, IQuS, via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science under Award DE-SC0020970, and by the National Science Foundation, NSF DMR-2300172.
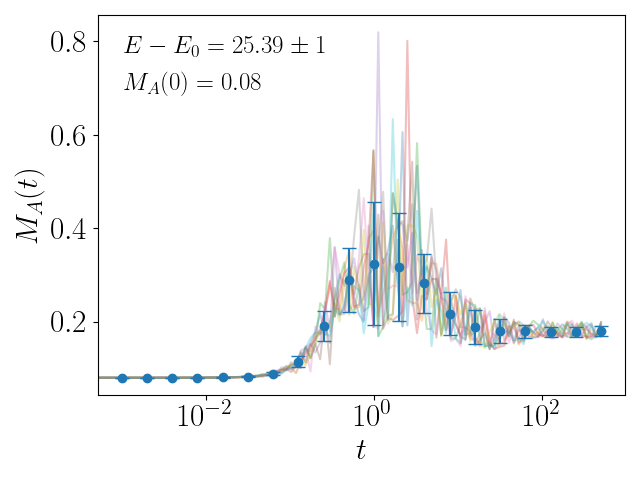
Entanglement Properties of SU(2) Gauge Theory
We review recent and present new results on thermalization of nonabelian gauge theory obtained by exact numerical simulation of the real-time dynamics of two-dimensional SU(2) lattice gauge theory. We discuss: (1) tests confirming the Eigenstate Thermalization Hypothesis; (2) the entanglement entropy of sublattices, including the Page curve, the transition from area to volume scaling with increasing energy of the eigenstate and its time evolution that shows thermalization of localized regions to be a two-step process; (3) the absence of quantum many-body scars for j(max)>1/2; (4) the spectral form factor, which exhibits the expected slope-ramp-plateau structure for late times; (5) the entanglement Hamiltonian for SU(2), which has properties in accordance with the Bisognano-Wichmann theorem; and (6) a measure for non-stabilizerness or “magic” that is found to reach its maximum during thermalization. We conclude that the thermalization of nonabelian gauge theories is a promising process to establish quantum advantage.
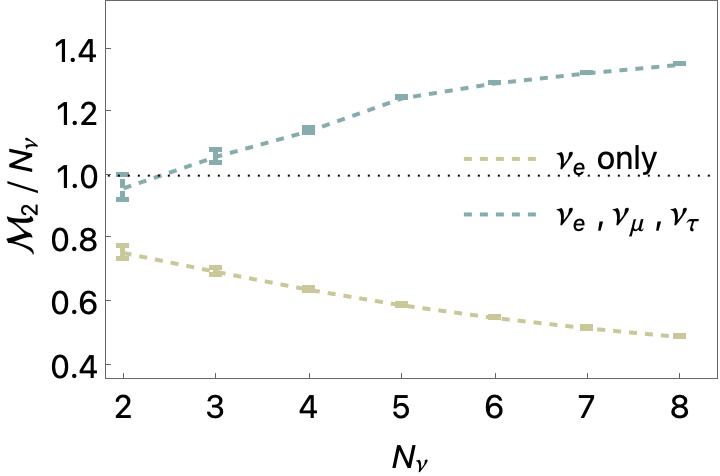
Quantum Magic and Computational Complexity in the Neutrino Sector
We consider the quantum magic in systems of dense neutrinos undergoing coherent flavor transformations, relevant for supernova and neutron-star binary mergers. Mapping the three flavor-neutrino system to qutrits, the evolution of quantum magic is explored in the single scattering angle limit for a selection of initial tensor-product pure states for N< 8 neutrinos. For initial states of electron-type neutrinos, the magic, as measured by the M(2) stabilizer Renyi entropy, is found to decrease with radial distance from the neutrino sphere, reaching a value that lies below the maximum for tensor-product qutrit states. Further, the asymptotic magic per neutrino, M(2)/N, decreases with increasing N. In contrast, the magic evolving from states containing all three flavors reaches values only possible with entanglement, with the asymptotic M(2)/N increasing with N. These results highlight the connection between the complexity in simulating quantum physical systems and the parameters of the Standard Model.
We would like to thank Vincenzo Cirigliano, Henry Froland and Niklas Müller for useful discussions, as well as Emanuele Tirrito for his inspiring presentation at the IQuS workshop Pulses, Qudits and Quantum Simulations, co-organized by Yujin Cho, Ravi Naik, Alessandro Roggero and Kyle Wendt, and for subsequent discussions, an also related discussions with Alessandro Roggero and Kyle Wendt. We would further thank Alioscia Hamma, Thomas Papenbrock and Rahul Trivedi for useful discussions during the IQuS workshop Entanglement in Many-Body Systems: From Nuclei to Quantum Computers and Back, co-organized by Mari Carmen Bañuls, Susan Coppersmith, Calvin Johnson and Caroline Robin. This work was supported by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science, and by the Department of Physics and the College of Arts and Sciences at the University of Washington (Ivan and Martin). This work was also supported, in part, by Universität Bielefeld, and by ERC-885281-KILONOVA Advanced Grant (Caroline). This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 using NERSC awards NP-ERCAP0027114 and NP-ERCAP0029601.
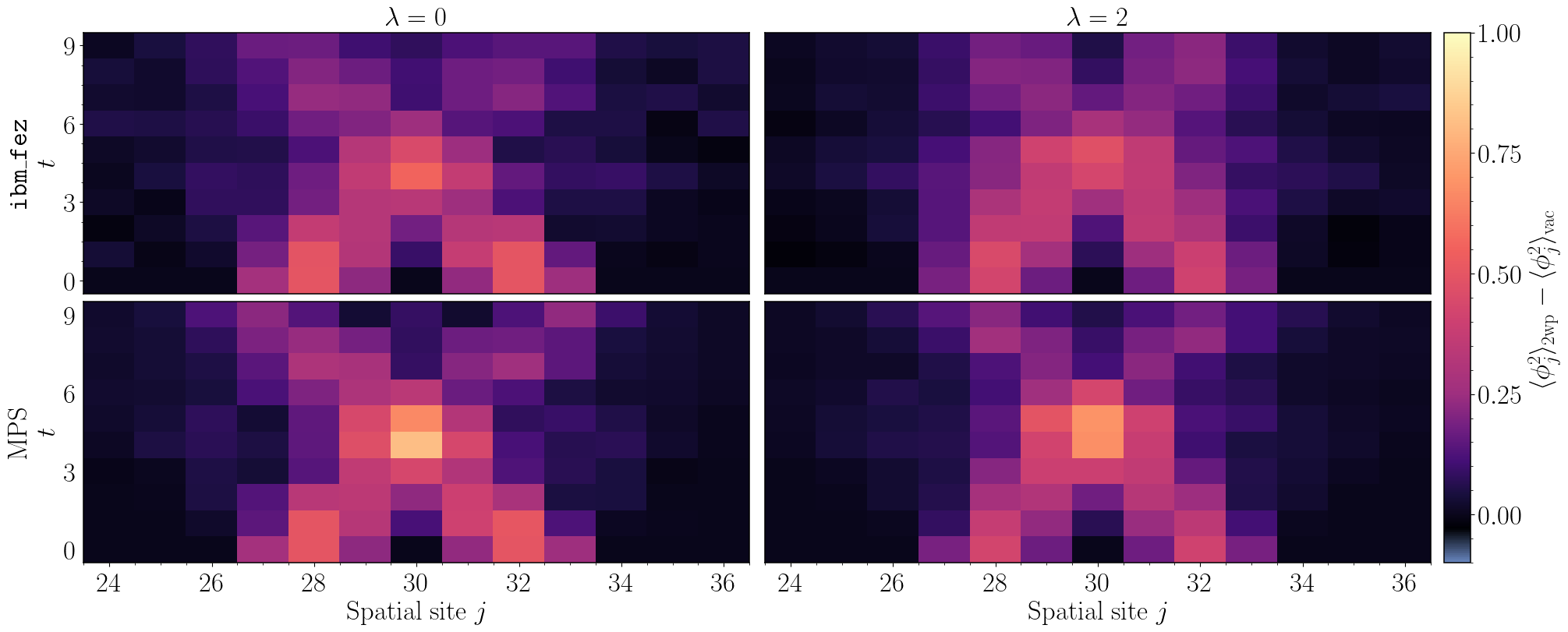
Scalable Quantum Simulations of Scattering in Scalar Field Theory on 120 Qubits
Simulations of collisions of fundamental particles on a quantum computer are expected to have an exponential advantage over classical methods and promise to enhance searches for new physics. Furthermore, scattering in scalar field theory has been shown to be BQP-complete, making it a representative problem for which quantum computation is efficient. As a step toward large-scale quantum simulations of collision processes, scattering of wavepackets in one-dimensional scalar field theory is simulated using 120 qubits of IBM’s Heron superconducting quantum computer ibm_fez. Variational circuits compressing vacuum preparation, wavepacket initialization, and time evolution are determined using classical resources. By leveraging physical properties of states in the theory, such as symmetries and locality, the variational quantum algorithm constructs scalable circuits that can be used to simulate arbitrarily-large system sizes. A new strategy is introduced to mitigate errors in quantum simulations, which enables the extraction of meaningful results from circuits with up to 4924 two-qubit gates and two-qubit gate depths of 103. The effect of interactions is clearly seen, and is found to be in agreement with classical Matrix Product State simulations. The developments that will be necessary to simulate high-energy inelastic collisions on a quantum computer are discussed.
The author thanks Roland Farrell, Marc Illa, Zhiyao Li, Henry Froland, Anthony Ciavarella, and Martin Savage for helpful discussions and insightful comments. This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. This work was also supported, in part, through the Department of Physics and the College of Arts and Sciences at the University of Washington. This work has made extensive use of Wolfram Mathematica, python, julia, jupyter notebooks in the conda environment, IBM’s quantum programming environment qiskit, and iTensor in this work. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. This research was done using services provided by the OSG Consortium, which is supported by the National Science Foundation awards #2030508 and #1836650. The author acknowledges the use of IBM Quantum Credits for this work. The views expressed are those of the author, and do not reflect the official policy or position of IBM or the IBM Quantum team.
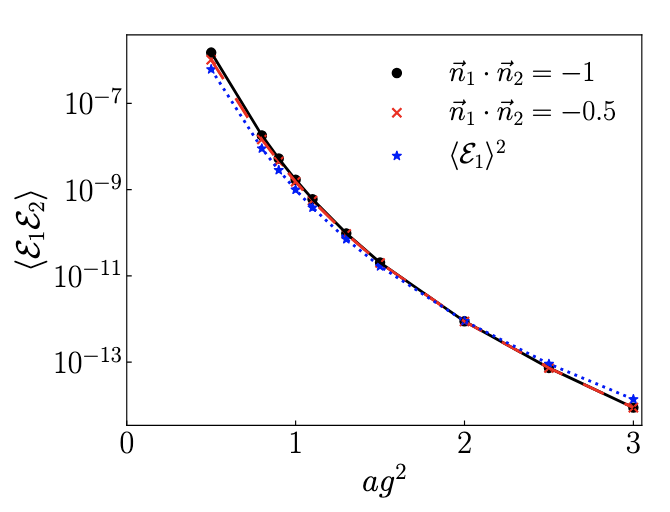
Quantum Computing for Energy Correlators
We study a quantum algorithm to calculate energy correlators for quantum field theories, which consists of ground state preparation, applying source, sink, energy flux and real-time evolution operators and Hadamard test. We discuss how to take the asymptotic detector limit in the Hamiltonian lattice approach. We then calculate the energy correlators for the SU(2) pure gauge theory in 2+1 dimensions on 3 x 3 and 5 x 5 honeycomb lattices with j_max=1/2 at fixed couplings, by using both classical methods and the quantum algorithm studied. The results obtained from the quantum algorithm and the IBM emulator are consistent with the classical methods’ results. We lay out the path forward for calculations in the physical limit.
K.L. was supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics from DE-SC0011090. F.T. and X.Y. were supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0027114.


