IQuS Publications
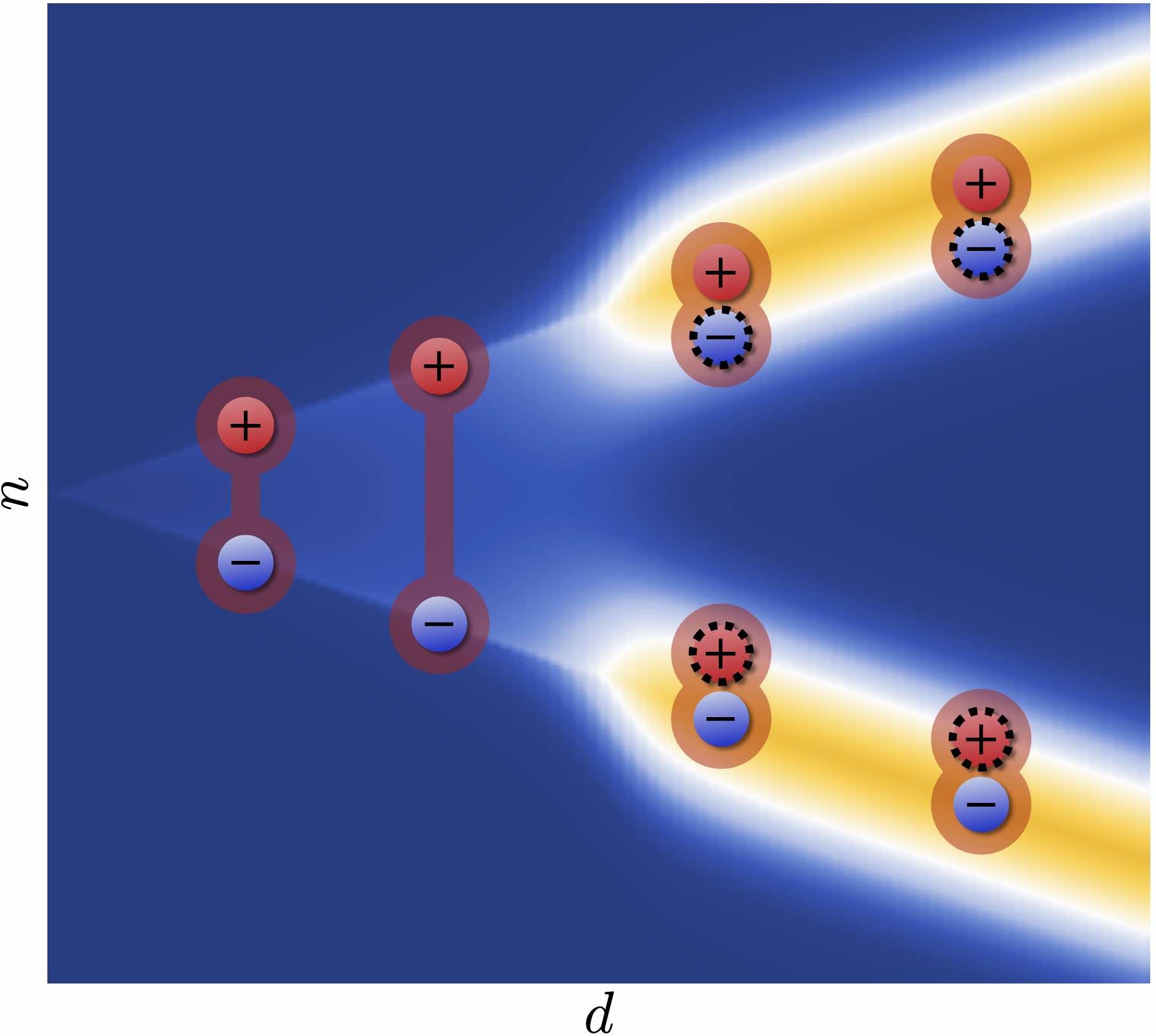
The Quantum Complexity of String Breaking in the Schwinger Model
String breaking, the process by which flux tubes fragment into hadronic states, is a hallmark of confinement in strongly-interacting quantum field theories. We examine a suite of quantum complexity measures using Matrix Product States to dissect the string breaking process in the 1+1D Schwinger model. We demonstrate the presence of nonlocal quantum correlations along the string that may affect fragmentation dynamics, and show that entanglement and magic offer complementary perspectives on string formation and hadronization beyond conventional observables.
We would like to thank Roland Farrell, Henry Froland, Tobias Haug, Dima Kharzeev, Eliana Marroquin and
Caroline Robin for helpful discussions. This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science. Sebastian was supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, Grants No. DE-FG02-97ER-41014 and in part by a Feodor Lynen Research fellowship of the Alexander von Humboldt foundation. This work was also supported, in part, by the Department of Physics and the College of Arts and Sciences at the University of Washington. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0032083. This research was done using services provided by the OSG Consortium, which is supported by the National Science Foundation awards #2030508 and #1836650. We have made use of the ITensor library for tensor network computations.
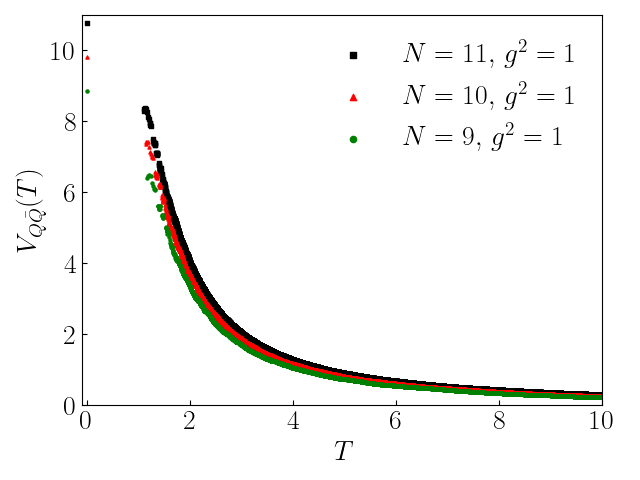
Minimally Truncated SU(3) Lattice Gauge Theory and String Tension
We study SU(3) gauge theory on small lattices in the minimal (qutrit) electric field truncation retaining only the 1, 3, 3bar representations for the link variables. Explicit expressions are given for the Kogut-Susskind Hamiltonian for the square plaquette chain and the two-dimensional honeycomb lattice. Our formalism can be easily extended to the minimally truncated general SU(Nc) gauge theory. The addition of (static) quarks is discussed. We present results for the energy spectrum of the gauge field on these lattices by exact diagonalization of the Hamiltonian and analyze its statistical properties. We also compute the SU(3) string tension and discuss how it is modified by vacuum fluctuations. Finally, we calculate the potential energies of a static quark-antiquark pair and three static quarks and study their screening at finite temperature.
Simulating Fully Gauge-Fixed SU(2) Hamiltonian Dynamics on Digital Quantum Computers
Quantum simulations of many-body systems offer novel methods for probing the dynamics of the Standard Model and its constituent gauge theories. Extracting low-energy predictions from such simulations rely on formulating systematically-improvable representations of lattice gauge theory Hamiltonians that are efficient at all values of the gauge coupling. One such candidate representation for SU(2) is the fully gauge-fixed Hamiltonian defined in the mixed basis. This work focuses on the quantum simulation of the smallest non-trivial system: two plaquettes with open boundary conditions. A mapping of the continuous gauge field degrees of freedom to qubit-based representations is developed. It is found that as few as three qubits per plaquette is sufficient to reach percent-level precision on predictions for observables. Two distinct algorithms for implementing time evolution in the mixed basis are developed and analyzed in terms of quantum resource estimates. One algorithm has favorable scaling in circuit depth for large numbers of qubits, while the other is more practical when qubit count is limited. The second algorithm is used in the measurement of a real-time observable on IBM’s Heron superconducting quantum processor, ibm_fez. The quantum results match classical predictions at the per-mille level. This work lays out the path forward for two- and three-dimensional simulations of larger systems, as well as demonstrating the viability of mixed-basis formulations for studying the properties of SU(2) gauge theories at all values of the gauge coupling.
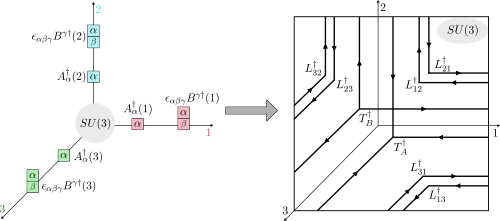
Loop-string-hadron approach to SU(3) lattice Yang-Mills theory, II: Operator representation for the trivalent vertex
This work is the second installment of a series on the Loop-String-Hadron (LSH) approach to SU(3) lattice Yang-Mills theory. Here, we present the infinite-dimensional matrix representation for arbitrary gauge-invariant operators at a trivalent vertex, which results in a standalone framework for computations that supersedes the underlying Schwinger-boson framework. To that end, we evaluate in closed form the result of applying any gauge-invariant operators on the LSH basis states introduced in Part I. Classical calculations in the LSH basis run significantly faster than equivalent calculations performed using Schwinger bosons. A companion code script is provided, which implements the derived formulas and aims to facilitate rapid progress towards Hamiltonian-based calculations of quantum chromodynamics.
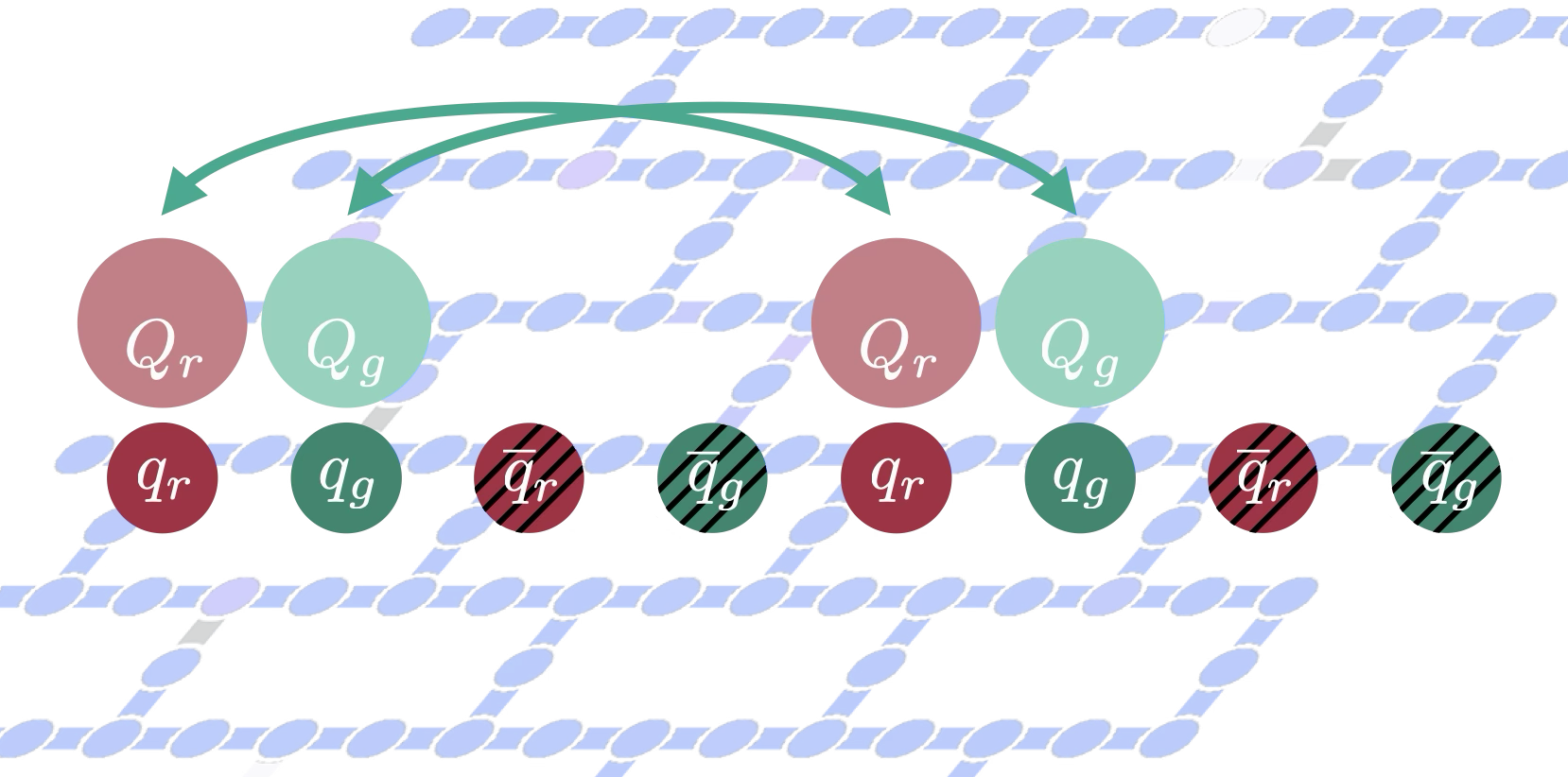
A Framework for Quantum Simulations of Energy-Loss and Hadronization in Non-Abelian Gauge Theories: SU(2) Lattice Gauge Theory in 1+1D
Simulations of energy loss and hadronization are essential for understanding a range of phenomena in non-equilibrium strongly-interacting matter. We establish a framework for performing such simulations on a quantum computer and apply it to a heavy quark moving across a modest-sized 1+1D SU(2) lattice of light quarks. Conceptual advances with regard to simulations of non-Abelian versus Abelian theories are developed, allowing for the evolution of the energy in light quarks, of their local non-Abelian charge densities, and of their multi-partite entanglement to be computed. The non-trivial action of non-Abelian charge operators on arbitrary states suggests mapping the heavy quarks to qubits alongside the light quarks, and limits the heavy-quark motion to discrete steps among spatial lattice sites. Further, the color entanglement among the heavy quarks and light quarks is most simply implemented using hadronic operators, and Domain Decomposition is shown to be effective in quantum state preparation. Scalable quantum circuits that account for the heterogeneity of non-Abelian charge sectors across the lattice are used to prepare the interacting ground-state wavefunction in the presence of heavy quarks. The discrete motion of heavy quarks between adjacent spatial sites is implemented using fermionic SWAP operations. Quantum simulations of the dynamics of a system on L=3 spatial sites are performed using IBM’s ibm_pittsburgh quantum computer using 18 qubits, for which the circuits for state preparation, motion, and one second-order Trotter step of time evolution have a two-qubit depth of 398 after transpilation. A suite of error mitigation techniques are used to extract the observables from the simulations, providing results that are in good agreement with classical simulations. The framework presented here generalizes straightforwardly to other non-Abelian groups, including SU(3) for quantum chromodynamics.
We would like to thank Roland Farrell, Henry Froland and Nikita Zemlevskiy for helpful discussions. This work was supported, in part, by U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science, by the Quantum Science Center (QSC) which is a National Quantum Information Science Research Center of the U.S Department of Energy, and by PNNL’s Quantum Algorithms and Architecture for Domain Science (QuAADS) Laboratory Directed Research and Development (LDRD) Initiative. The Pacific Northwest National Laboratory is operated by Battelle for the U.S. Department of Energy under Contract DE-AC05 76RL01830. It was also supported, in part, by the Department of Physics and the College of Arts and Sciences at the University of Washington. This research used resources of the Oak Ridge Leadership Computing Facility (OLCF), which is a DOE Office of Science User Facility supported under Contract DE AC05-00OR22725. We acknowledge the use of IBM Quantum services for this work. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team. This work was enabled, in part, by the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. We have made extensive use of Wolfram Mathematica, python, julia, jupyter notebooks in the Conda environment, and IBM’s quantum programming environment qiskit. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award NP-ERCAP0032083.

Quantum Error Correction Codes for Truncated SU(2) Lattice Gauge Theories
We construct two quantum error correction codes for pure SU(2) lattice gauge theory in the electric basis truncated at the electric flux $j_{\rm max}=1/2$, which are applicable on quasi-1D plaquette chains, 2D honeycomb and 3D triamond and hyperhoneycomb lattices. The first code converts Gauss’s law at each vertex into a stabilizer while the second only uses half vertices and is locally the carbon code. Both codes are able to correct single-qubit errors. The electric and magnetic terms in the SU(2) Hamiltonian are expressed in terms of logical gates in both codes. The logical-gate Hamiltonian in the first code exactly matches the spin Hamiltonian for gauge singlet states found in previous work.
We would like to thank Alessandro Roggero for use- ful discussions. We acknowledge the workshop “Co- design for Fundamental Physics in the Fault-Tolerant Era” held at the InQubator for Quantum Simulation (IQuS)3 hosted by the Institute for Nuclear Theory in April 2025. This work is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, IQuS under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science
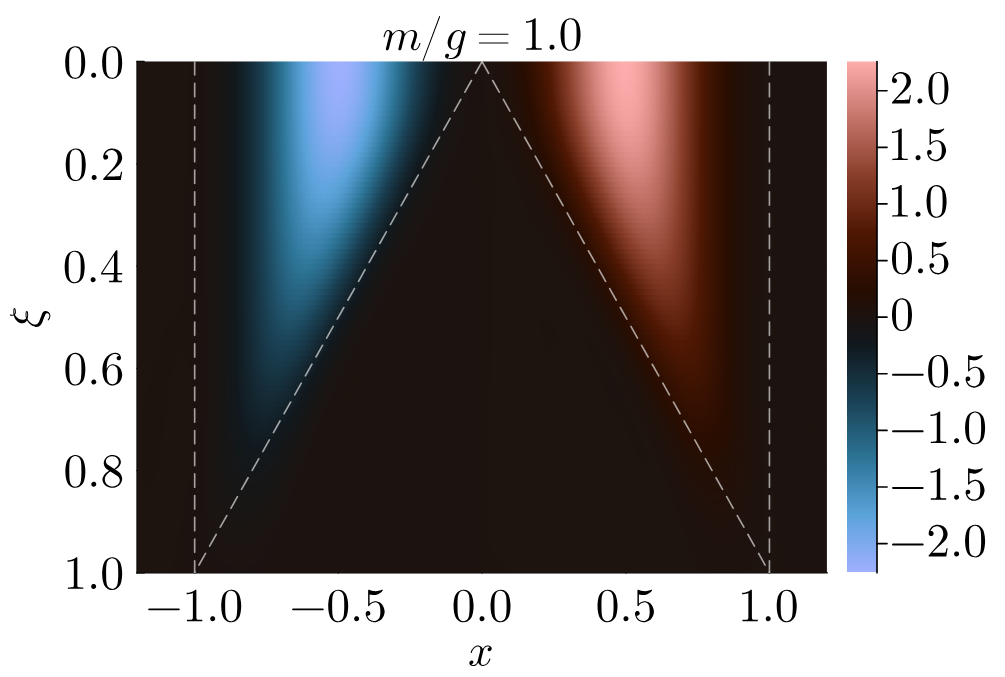
Tensor network simulations of quasi-GPDs in the massive Schwinger model
Generalized Parton Distribution functions (GPDs) are light-cone matrix elements that encode the internal structure of hadrons in terms of quark and gluon degrees of freedom. In this work, we present the first nonperturbative study of quasi-GPDs in the massive Schwinger model, quantum electrodynamics in 1+1 dimensions (QED2), within the Hamiltonian formulation of lattice field theory. Quasi-distributions are spatial correlation functions of boosted states, which approach the relevant light-cone distributions in the luminal limit. Using tensor networks, we prepare the first excited state in the strongly coupled regime and boost it to finite momentum on lattices of up to 400 lattice sites.
We compute both quasiparton distribution functions and, for the first time, quasi-GPDs, and study how they converge with increasing boost and in the continuum limit. In addition, we perform analytic calculations of GPDs in the two-particle Fock-space approximation and in the Reggeized limit, providing qualitative benchmarks for the tensor network results. Our analysis establishes computational benchmarks for accessing partonic observables in low-dimensional gauge theories, offering a starting point for future extensions to higher dimensions, non-Abelian theories, and quantum simulations.
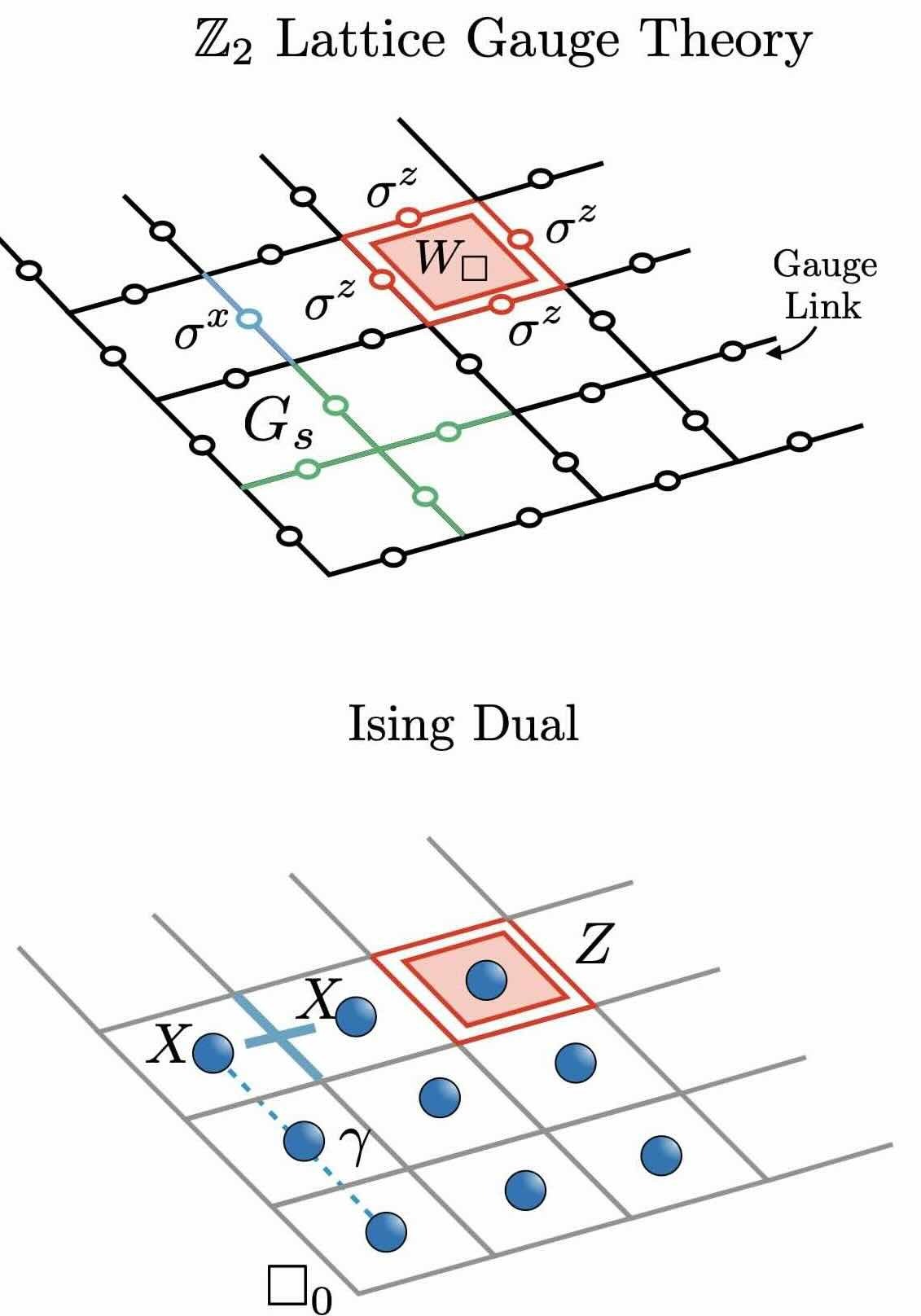
Classical shadows for sample-efficient measurements of gauge-invariant observables
Classical shadows provide a versatile framework for estimating many properties of quantum states from repeated, randomly chosen measurements without requiring full quantum state tomography. When prior information is available—such as knowledge of symmetries of states and operators—this knowledge can be exploited to significantly improve sample efficiency. In this work, we develop three classical shadow protocols tailored to systems with local (or gauge) symmetries to enable efficient prediction of gauge-invariant observables in lattice gauge theory models which are currently at the forefront of quantum simulation efforts. For such models, our approaches can offer exponential improvements in sample complexity over symmetry-agnostic methods, albeit at the cost of increased circuit complexity. We demonstrate these trade-offs using a Z2 lattice gauge theory, where a dual formulation enables a rigorous analysis of resource requirements, including both circuit depth and sample complexity.
We thank Hong-Ye Hu, Jonathan Kunjummen, Martin Larocca, and Yigit Subasi for helpful discussions. J.B. thanks the Harvard Quantum Initiative for support. N.M. (during early stages) and H.F. acknowledge funding by the DOE, Office of Science, Office of Nuclear Physics, IQuS (https://iqus.uw. edu), via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science under Award DE-SC0020970. J.B. notes that the views expressed in this work are those of the author and do not reflect the official policy or position of the U.S. Naval Academy, Department of the Navy, the Department of Defense, or the U.S. Government.
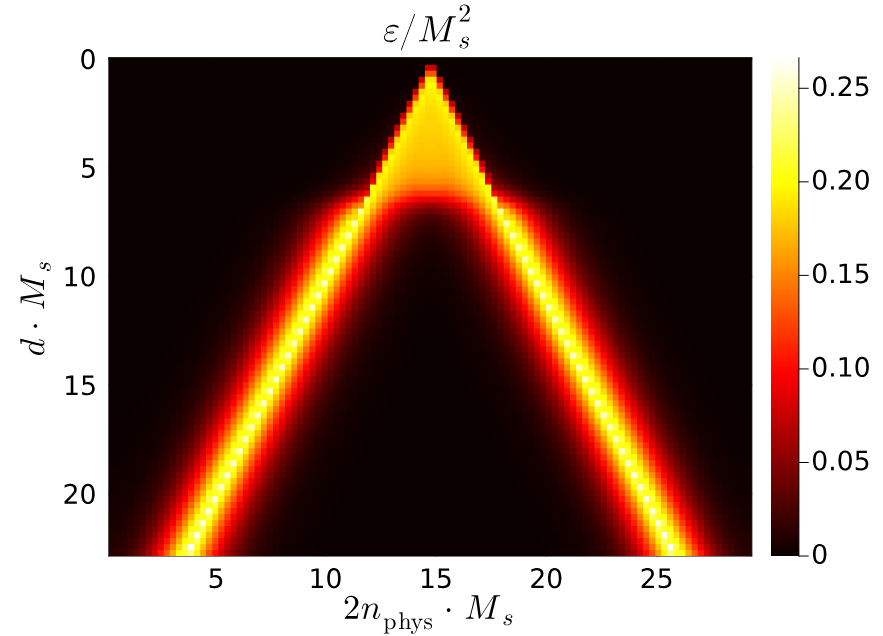
Thermal nature of confining strings
We investigate the quantum statistical properties of the confining string connecting a static fermion-antifermion pair in the massive Schwinger model. By analyzing the reduced density matrix of the subsystem located in between the fermion and antifermion, we demonstrate that as the interfermion separation approaches the string-breaking distance, the overlap between the microscopic density matrix and an effective thermal density matrix exhibits a pronounced, narrow peak, approaching unity at the onset of string breaking. This behavior reveals that the confining flux tube evolves toward a genuinely thermal state as the separation between the charges grows, even in the absence of an external heat bath.
In other words, one cannot tell whether a reduced state of the subsystem arises from a surrounding heat bath or from entanglement with the rest of the system. The entanglement spectrum near the critical string-breaking distance exhibits a rapid transition from the dominance of a single state describing the confining electric string towards a strongly entangled state containing virtual fermion-antifermion pairs.
Our findings establish a quantitative link between confinement, entanglement, and emergent thermality, and suggest that string breaking corresponds to a microscopic thermalization transition within the flux tube.
We are grateful to Adrien Florio, David Frenklakh and Shuzhe Shi for useful discussions and collaboration on related work. We also thank the participants of the QuantHep2025 workshop at Lawrence Berkeley National Lab for insightful comments. This work was supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, Grants No. DE-SC0020970 (InQubator for Quantum Simulation (IQuS), S.G.), DE-FG02-97ER- 41014 (UW Nuclear Theory, S.G.), DE-FG88ER41450 (SBU Nuclear Theory, D.K., E.M.) and by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Co-design Center for Quantum Advantage (C2QA) under Contract No.DE-SC0012704 (S.G., D.K., E.M.). S.G. was supported in part by a Feodor Lynen Research fellowship of the Alexander von Humboldt foundation. E.M. was supported in part by the Center for Distributed Quantum Processing at Stony Brook University.

The Magic Barrier before Thermalization
We investigate the time dependence of anti-flatness in the entanglement spectrum, a measure for non-stabilizerness and lower bound for non-local quantum magic, on a subsystem of a linear SU(2) plaquette chain during thermalization. Tracing the time evolution of a large number of initial states, we find that the anti-flatness exhibits a barrier-like maximum during the time period when the entanglement entropy of the subsystem grows rapidly from the initial value to the microcanonical entropy. The location of the peak is strongly correlated with the time when the entanglement exhibits the strongest growth. This behavior is found for generic highly excited initial computational basis states and persists for coupling constants across the ergodic regime, revealing a universal structure of the entanglement spectrum during thermalization. We conclude that quantitative simulations of thermalization for nonabelian gauge theories require quantum computing. We speculate that this property generalizes to other quantum chaotic systems.
The authors gratefully acknowledge the scientific support and HPC resources provided by the Erlangen National High Performance Computing Center (NHR@FAU) of the Friedrich-Alexander-Universita ̈t Erlangen-Nu ̈rnberg(FAU).B.M.acknowledgessupport by the U.S. Department of Energy, Office of Science (grant DE-FG02-05ER41367). X.Y. is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, InQubator for Quantum Simulation (IQuS) (https://iqus.uw.edu) under Award Number DOE (NP) Award DE-SC0020970 via the program on Quantum Horizons: QIS Research and Innovation for Nuclear Science and acknowledges the discussions at the “Many-Body Quantum Magic” workshop held at the IQuS hosted by the Institute for Nuclear Theory in Spring 2025. L.E. acknowledges funding by the Max Planck Society, the Deutsche Forschungsgemein- schaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2111 – 390814868, and the European Research Council (ERC) under the European Union’s Horizon Europe research and innovation program (Grant Agreement No. 101165667)—ERC Starting Grant QuSiGauge. Views and opinions expressed are those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. This work is part of the Quantum Computing for High-Energy Physics (QC4HEP) working group. C.S. would like to thank the organizers and participants of the QuantHEP 2025 conference at Lawrence Berkeley National Lab for valuable discussions that contributed to this work.


